В этой части обзора, являющегося продолжением тем

• О принципах в физике
• Голографическая принцип - первая встреча
• Термодинамика чёрных дыр

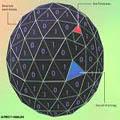
Рассмотрим голографический экран и частицу массы $m,$ приближающуюся к нему. Согласно голографическому принципу частица влияет на количество информации (и, следовательно, на энтропию), которая запасена на экране. Естественно предположить, что изменение энтропии вблизи экрана линейно по смещению $\Delta x,$, $$\Delta S=2\pi k_{_B}\frac{mc}{\hbar }\Delta x.$$ Причина введения фактора $2\pi $ будет ясна ниже. Чтобы понять, почему эта величина пропорциональна массе, давайте представим, что частица расщепилась на две или более частиц меньшей массы. Каждая из частиц тогда переносит своё собственное изменение энтропии при сдвиге на $\Delta x.$

Так как и энтропия и масса аддитивны, то, естественно, что энтропия пропорциональна массе. В силу первого закона термодинамики энтропийная сила, связанная с изменением информации подчиняется соотношению $$F\Delta x=T\Delta S.$$ Если нам известен градиент энтропии (его можно найти, используя $\Delta S$, то, зная температуру экрана, мы можем вычислить энтропийную силу. Как известно, наблюдатель, движущийся с ускорением $a,$ ощущает температуру $T_{U}$, $$ k_{_B}T=\frac{1}{2\pi }\frac{\hbar }{c}a $$ Предположим, что полная энергия системы $E.$ Сделаем простое предположение, что энергия равномерно распределена по всем $N$ битам информации на голографическом экране. Температура тогда определяется, как средняя энергия на бит $$E=\frac{1}{2}N k_{_B}T.$$ Эти формулы позволяют построить голографическую динамику и, как, частный случай -- динамику Вселенной, не используя понятия гравитации. Давайте воспроизведём в рамках этой схемы ряд фундаментальных физических законов.
Второй законы Ньютона
Энтропийная сила, действующая на пробную частицу массы $m,$ приближающуюся к голографическому экрану с температурой $T$ равна $$F=T\frac{\Delta S}{\Delta x}=2\pi k_{_B}\frac{mc}{\hbar }T$$

Трактуя температуру $T$ как температуру Унру $T_{U}$ получим второй закон Ньютона $$F=ma.$$ В рамках этой же схемы может быть получен и первый закон Ньютона - закон инерции.

Закон инерции
Вернёмся опять к примеру частицы массы $m,$ приближающейся к голографическому экрану. В какой-то момент она должна слиться с микроскопическими степенями свободы на экране, и, следовательно, она будет состоять из тех же битов, которые живут на экране. Так как каждый бит переносит энергию $\frac{1}{2}k_{_B}T,$ то должно выполняться соотношение $$mc^2=\frac{1}{2}n{k_{_B}}T.$$ Если мы подставим это выражение в $F$ и используем $T_{U}$ мы выразим изменение энтропии в терминах ускорения $$\frac{\Delta S}{n\Delta x}=k_{_B}\frac{a}{2c^2}$$ Это уравнение представляет 'голографическую' трактовку закона инерции: если отсутствуют градиенты энтропии, то отсутствуют энтропийные силы и, как следствие, ускорение тела равно нулю. Закон Всемирного тяготения Давайте теперь, используя голографический принцип, получим закон всемирного тяготения.

Пусть теперь частица массы $m$ приближается к сферическому голографическому экрану. На неё по-прежнему действует энтропийная сила $$F=T\frac{\Delta S}{\Delta x}=2\pi T{{k}_{B}}\frac{mc}{\hbar }$$ где $T$ -- температура голографического экрана. Используем закон равнораспределения энергии по степеням свободы $$E=\frac{1}{2}N{{k}_{B}}T$$ Здесь $N$ -- число степеней свободы на экране, которое согласно голографическому принципу равно (точнее не может превосходить) $$N=\frac{Ac^3}{G\hbar }=\frac{4\pi R^2}{c^3}{G\hbar }$$ Понимая под $E$ величину $Mc^2,$ где $M$ -- масса, сосредоточенная в области, ограниченной голографическим экраном, получим для температуры $$T=\frac{Mc^2}{2k_{_B}}\pi R^2\frac{G\hbar }{c^3}$$ Подставляя температуру в исходное выражение для энтропийной силы, воспроизведём закон всемирного тяготения $$F=G\frac{mM}{R^2}.$$

Подчеркнём важность этого результата: гравитационные силы возникли в теории, которая первоначально не содержала гравитации и ничего не знала о ее существовании. Мы получили убедительную количественную поддержку предположения о энтропийной природе гравитации.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.