За квантовым горизонтом
Когда-то считалось, что квантовая теория устанавливает абсолютный предел нашим знаниям и развитию техники, но сегодня она расширяет вычислительную мощь компьютеров и возможности человеческого разума.

В конце XIX в. неизвестный художник изобразил путешественника, который достиг горизонта, где небо встречается с землей. Стоя на коленях на фоне стилизованного земного пейзажа, головой он пробивает небесную твердь, чтобы лицезреть неизведанное. Изображение, известное как "Гравюра Фламмариона", иллюстрирует поиски человеком знания. Две возможные интерпретации этой визуальной метафоры соответствуют двум диаметрально различным концепциям знания.
На гравюре изображен либо воображаемый барьер, который в действительности наука всегда в состоянии преодолеть, либо барьер настоящий, который мы можем перейти лишь в воображении. При последнем прочтении художник как бы говорит нам, что мы пленники, заключенные внутри конечного купола известных объектов и событий. Возможно, мы сумеем понять мир непосредственных впечатлений, но бесконечность снаружи для нас непостижима и не поддается объяснению. Действительно ли наука постоянно выходит за пределы известного и открывает новые горизонты, или она показывает нам, что из нашей тюрьмы выхода нет, преподавая нам урок ограниченного знания и неограниченного смирения?
ОБ АВТОРАХ
 Дэвид Дойч (David Deutsch), физик из Оксфордского университета, который придумал концепцию универсального квантового компьютера, говорит, что он заинтересовался физикой еще в детском возрасте, когда воспротивился утверждению, что никто не может понять все, что понятно.
Дэвид Дойч (David Deutsch), физик из Оксфордского университета, который придумал концепцию универсального квантового компьютера, говорит, что он заинтересовался физикой еще в детском возрасте, когда воспротивился утверждению, что никто не может понять все, что понятно.
 Артур Экерт (Artur Ekert), еще будучи студентом-старшекурсником, выполнил пионерские работы по криптографии на основе квантового перепуты-вания. Сейчас он директор Центра квантовой технологии в Сингапуре и профессор Оксфордского математического института. Он увлекается пилотированием и глубоководными погружениями.
Артур Экерт (Artur Ekert), еще будучи студентом-старшекурсником, выполнил пионерские работы по криптографии на основе квантового перепуты-вания. Сейчас он директор Центра квантовой технологии в Сингапуре и профессор Оксфордского математического института. Он увлекается пилотированием и глубоководными погружениями.
Квантовую теорию часто приводят в качестве неопровержимого аргумента в пользу последнего. На заре становления квантовой механики у теоретиков родилась традиция с серьезным видом сознательно учить студентов иррациональному взгляду на мир: "Если вы думаете, что понимаете квантовую теорию, то вы ее не понимаете", "Вы не должны задавать этот вопрос", "Эта теория непостижима, как и сам мир", "Все это происходит без причины и не имеет объяснения"... Так обычно писалось в учебниках и статьях для научно-популярных изданий.
Однако исследования минувших двух десятилетий опровергают такие представления. На протяжении истории развития этой области науки физики часто предполагали, что разного рода ограничения квантовой физики не позволят нам покорить природу в полной мере, как это было принято считать ранее в классической механике. Но ни одно из таких препятствий так и не материализовалось. Наоборот, квантовая механика освобождалась. По существу, квантовомеханические свойства объектов, такие как суперпозиция, перепутывание, дискретность и случайность, оказались не ограничительными факторами, а дополнительные ресурсами. Пользуясь ими, изобретатели создали множество разных удивительных приборов, таких как лазеры и полупроводниковые интегральные схемы.
Но это было только начало. Мы во все большей степени используем квантовые явления в связи и в вычислительных системах, которые недоступны пониманию с классической точки зрения. Мы открываем новые пути покорения природы и даже обретения знаний.
За пределами неопределенности
В 1965 г. сооснователь компании Intel Гордон Мур (Gordon Moore) предсказал, что инженеры будут удваивать число транзисторов на полупроводниковой интегральной схеме примерно каждые два года. Известное сегодня как закон Мура, это предсказание оставалось верным в течение более чем полстолетия. Однако уже с самого начала был слышен звон тревожного колокола. Если закон будет оставаться верным и впредь, то можно предсказать время, когда транзисторы достигнут размеров отдельных атомов, — и что тогда? Инженеры столкнутся со сферой непознаваемого.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
- Квантовую механику раньше рассматривали как теорию ограничений, подразумевая под этим то, что нашим наблюдениям неизбежно присуща неопределенность, что миром правит случайность и что сама по себе теория слишком странна для того, чтобы ее понять, и заставляет нас в принципе отказаться от идеи о том, что наука в состоянии описать окружающий нас мир.
- Эти ложные представления своими корнями уходят в философские доктрины, такие как логический позитивизм, которые были популярны в период, когда физика разрабатывала и оттачивала эту теорию.
- В действительности квантовая механика не налагает существенных ограничений. Квантовый мир достаточно богат и сложен, чтобы позволить нам создать новую практичную технику и обрести множество новых знаний.
В традиционной формулировке квантовой механики принцип неопределенности устанавливает предел, который никакой технический прогресс преодолеть не в силах: чем больше мы знаем о каких-то свойствах, таких как положение частицы, тем меньше догадываемся о других, таких как ее скорость. А тем, чего мы не знаем, нельзя управлять. Попытки манипулировать крошечными объектами сталкиваются с безудержной хаотичностью, невозможными в классической физике взаимосвязями, а также нарушениями причинно-следственных связей. Отсюда следовал неизбежный вывод: конец развития информационных технологий уже не за горами.
Однако сегодня физики в рабочем порядке управляют миром квантовых явлений без каких-либо подобных ограничений. Мы записываем информацию в отдельных атомах или элементарных частицах и обрабатываем ее с невероятной точностью, несмотря на принцип неопределенности, очень часто достигая функциональности, недостижимой любым другим методом. Но каким образом?
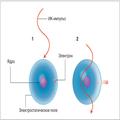
Давайте поближе рассмотрим базисную в традиционном понимании единицу информации: бит. Для физика бит — это физическая система, которую можно перевести в одно из двух различных состояний, представляющих собой два логических значения: "да" или "нет", "правда" или "ложь", "0" или "1". В цифровых вычислительных машинах наличие или отсутствие заряда на пластинах конденсатора может соответствовать биту. На атомном уровне можно воспользоваться двумя состояниями электрона в атоме, так чтобы "0" соответствовал состоянию с самой низкой энергией (основному состоянию), а "1" какому-нибудь состоянию с более высокой энергией (возбужденному состоянию).
Чтобы управлять этой информацией, физики освещают атом импульсами света. Импульс правильно подобранной частоты, длины и амплитуды, называемый f-импульсом, переводит состояние из "0" в "1" и наоборот. Физики могут подобрать частоту и таким образом, чтобы воздействовать сразу на два связанных между собой атома, так что один атом управляет вторым. Таким образом, мы получили компоненты одно- и двухбитной логической ячейки, строительные блоки классической вычислительной машины, не испытав никаких козней со стороны принципа неопределенности.
Больше не непреодолимое препятствие
ВОЗМОЖНЫЕ ОГРАНИЧЕНИЯ КВАНТОВЫХ ВЫЧИСЛЕНИЙ И КАК ИХ ОБОЙТИ
Квантовая механика часто рисуется как непреодолимое препятствие на пути к миниатюризации электроники. К счастью, это не так. Физики научились обходить барьеры, которые раньше их беспокоили. На самом деле именно на квантовом уровне компьютеры смогут достичь своего истинного потенциала, обретя мощь, на голову превосходящую вычислительные возможности обычных машин.
Принцип неопределенности
ПРОБЛЕМА. Знаменитый принцип неопределенности Гейзенберга ограничивает точность некоторых измерений. Если точно зафиксировать положение частицы, то она начнет двигаться одновременно с разными скоростями, лежащими в определенном диапазоне. Если вы точно измеряете скорость частицы, то аналогичным образом вы заставляете ее "размыть" свое положение в пространстве неконтролируемым образом. Поэтому свойства эти — ненадежный способ хранения информации.
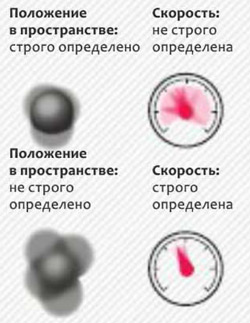
РЕШЕНИЕ. Не все квантовые измерения подвержены такого рода ограничениям. В ситуации, когда положение в пространстве и скорость неопределенны, строго определенное значение могут иметь другие величины, такие как энергия. В ситуации, где энергия имеет неопределенное значение, можно воспользоваться другими переменными.

Декогеренция
ПРОБЛЕМА. Частицы, из которых состоит компьютер, взаимодействуют с окружающим миром таким образом, что информация выходит за его пределы, нарушая процесс квантовых вычислений.
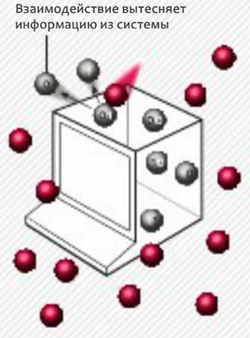
РЕШЕНИЕ. Методы коррекции ошибок могут компенсировать декогеренцию в течение достаточно большого времени для завершения вычислений. Например, физики могут записать информацию в нескольких частицах а) или закодировать ее в геометрическом виде, в виде структуры, обладающей естественной устойчивостью к шуму б).

Чтобы понять, что делает возможным это трюк миниатюризации, мы должны уяснить, что именно утверждает принцип неопределенности. В любой момент времени некоторые из характеристик атома или другой квантовой системы, называемые его или ее "наблюдаемыми", могут быть "четкими" — принимать в этот момент лишь одно-единственное значение. Принцип неопределенности не запрещает существование четких наблюдаемых. Он просто говорит, что не все наблюдаемые физической системы могут быть четкими в один и тот же момент времени. Например, в атоме четкая наблюдаемая— энергия: как в состоянии "0", так и в состоянии "1" электрон имеет строго определенную энергию. Другие наблюдаемые, такие как положение и скорость, нельзя назвать четкими. Электрон "размазан" в пространстве, и аналогичным образом его скорость одновременно принимает различные значения. Если для сохранения информации мы попытаемся воспользоваться его положением и скоростью, мы действительно столкнемся с квантовыми ограничениями. Ответ— не опускать в отчаянии руки, а сделать разумный выбор наблюдаемых, которые могут служить битами вычислительной машины.
Эта ситуация напоминает комическую сцену, когда пациент говорит врачу: "У меня болит, когда я делаю то-то", на что доктор отвечает: "Так не делайте этого". Если какие-то из свойств частицы трудно сделать четкими, то существует простой способ обойти это препятствие: не делайте попыток хранить информацию, используя эти свойства. Воспользуйтесь каким-нибудь другим из ее свойств.
За пределами битов
Если все, чего мы хотим добиться, — это построить классический компьютер, используя в качестве строительных блоков атомы, а не транзисторы, то четкие наблюдаемые — именно то, что нам необходимо. Но квантовая механика предлагает нам нечто гораздо большее. Она позволяет сделать мощный инструмент и на основе нечетких наблюдаемых. Тот факт, что наблюдаемые могут одновременно принимать множество значений, увеличивает наши возможности в огромной степени.
Например, энергия обычно— это четкая наблюдаемая, но мы можем превратить ее в нечеткую. Помимо того что электрон в атоме может находиться в основном или возбужденном состоянии, он может быть в состоянии суперпозиции — т.е. в обоих состояниях сразу. Электрон по-прежнему в строго определенном состоянии, но его состояние не "0" и не "1", а "0 и 1".
Это можно сделать с любым физическим объектом, но объект, в котором такие состояния можно надежно создать, измерить и ими управлять, называется квантовым битом, или кубитом. С помощью импульсов света энергию электрона можно изменять, переводя его не только из одного четкого состояния в другое, но и из четкого в нечеткое и наоборот. Если г-импульс меняет состояния "0" и "1", то импульс той же частоты, но в два раза короче или в два раз меньшей амплитуды, называемый $\pi /2$-импульсом, переводит электрон в суперпозицию состояний "0" и "1".
Если бы мы попытались измерить энергию электрона в таком состоянии суперпозиции, то мы с одинаковой вероятностью обнаружили бы, что он находится в основном или возбужденном состоянии. И тогда мы столкнулись бы со случайностью — именно так, как утверждают скептики. Опять-таки, мы легко можем обойти это очевидное препятствие — и тем самым добиться радикально новых функциональных возможностей. Вместо того чтобы измерять энергию электрона в этом состоянии суперпозиции, оставим все как есть. Например, возьмем электрон в состоянии "0" и направим на него $\pi /2$-импульс, а затем облучим его вторым $\pi /2$-импульсом. Измерим теперь энергию электрона. Он будет находиться в состоянии "1" со стопроцентной вероятностью. Наблюдаемая снова четкая.
Чтобы понять важность этого, давайте рассмотрим основной логический элемент компьютера, вентиль "НЕ". На его выходе — логическое отрицание входного сигнала: "0" он превращает в "1", а "1" в "0".
Допустим, вам дали следующее задание: сконструировать логический квадратный корень из "НЕ" — т.е. логическое устройство, которое дает на выходе отрицание, если подать на его вход сигнал два раза подряд. Используя только классическое оборудование, вы обнаружили бы, что задание невыполнимо. Однако $\pi /2$-импульс осуществляет эту "невозможную" логическую функцию. Два таких последовательных импульса дают в точности желаемый эффект. Физики-экспериментаторы построили этот и другие невозможные в рамках классической физики вентили, используя кубиты на основе фотонов, запертых ионов, атомов и ядерных спинов (Монро К., Уайнленд Д. Ионы для квантовых компьютеров -- ВМН, №11, 2008) Это строительные блоки квантового компьютера.
За пределами классических вычислений
Чтобы решить какую-нибудь задачу, компьютеры (классические или квантовые) выполняют строгую последовательность команд — алгоритм. Ученые, работающие в области теории вычислительных машин и систем, оценивают эффективность алгоритма по тому, как быстро растет время выполнения задачи, если на вход подаются все большие массивы данных. Например, используя алгоритм, который изучают в начальной школе, можно умножить два n-значных числа за время, которое растет как квадрат количества цифр в числе, $n^2$. В противоположность этому самый быстрый из известных методов выполнения обратной операции— факторизации, разложения n-значного числа на простые множители — требует времени, которое растет экспоненциально, примерно как $2^n$. Это считается неэффективным.
Квантовая логика
НЕВОЗМОЖНО... НЕТ!
Квантовые компьютеры могут делать не только то, что умеет классический компьютер, но и выполнять операции, выходящие за рамки классической логики. В данном случае два энергетических состояния электрона в атоме представляют "0" и "1" компьютерного бита. В обоих случаях у электрона нет определенного положения и скорости; он распределен вдоль сферической и овальной областей, называемых орбиталями, и его скорость одновременно лежит в некотором диапазоне скоростей. Тем не менее два состояния имеют различные энергии, и именно энергии задают значение бита.
Обычное "НЕ"
Чтобы выполнить элементарную вычислительную операцию "НЕ", которая инфер-тирует значение бита, физики освещают атом импульсом света определенной частоты, продолжительности и интенсивности, называемым $\pi$-импульсом. Если электрон находился в состоянии "0", то он перейдет в состояние "1", и наоборот.
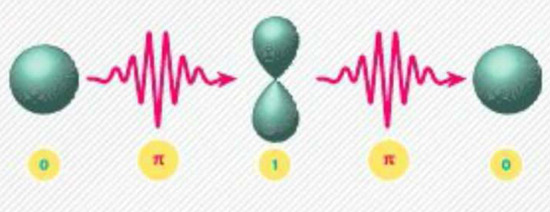
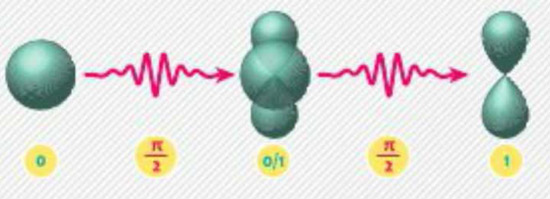
Квадратный корень из "НЕ"
Эту процедуру можно видоизменить, чтобы произвести, казалось бы, невозможную логическую операцию: извлечь квадратный корень из "НЕ". Так называемый $\pi /2$-импульс, меньшей амплитуды или более короткой продолжительности, чем $\pi$-импульс, переводит электрон из состояния "0" или "1" в их комбинацию, или, как говорят, суперпозицию обоих состояний. Второй $\pi /2$-импульс в свою очередь переводит электрон либо в состояние "1" (если первоначально было состояние "0"), либо в состояние "0" (если первоначально было состояние "1"). Эта и другие новые операции дают квантовому компьютеру огромную вычислительную мощь.
Предлагая качественно новые логические вентили, квантовая механика дает возможность использовать новые алгоритмы. Один из наиболее впечатляющих примеров — именно факторизация. Квантовый алгоритм, открытый в 1994 г. Питером Шором (Peter Shor), в то время работавшим в компании Bell Laboratories, позволяет разложить число на простые множители с помощью последовательности шагов, которая растет как $n^2$. При решении других задач, таких как поиск в длинном списке, квантовые компьютеры дают менее впечатляющее, но тем не менее значительное преимущество. Но, конечно, не все квантовые алгоритмы настолько эффективны, многие из них не быстрее, чем их классические аналоги (Ааронсон С. На что способны квантовые компьютеры? -- ВМН, № 6, 2008).
Вероятнее всего, первым практическим применением универсального квантового компьютера будет не факторизация, а моделирование других квантовых систем — задача, которая требует экспоненциально быстро растущего времени у классических компьютеров. Квантовое моделирование, возможно, окажет огромное влияние на такие области, как разработка новых лекарств и создание новых материалов.
Скептики, сомневающиеся в возможности практической реализации квантовых вычислений, говорят о больших трудностях сопряжения друг с другом квантовых логических вентилей. Кроме технических сложностей при работе в масштабе одного атома или одного фотона, главная проблема— предотвратить воздействие на вычислительный процесс окружающей среды. Об этом явлении, называемом декогерентностью (распадом суперпозиционных состояний. — Прим. пер.), часто говорят как о фундаментальном ограничении, налагаемом на квантовые вычисления. Но это не так. Сама квантовая теория дает средства для исправления ошибок, вызванных декогерентностью. Если источник ошибки удовлетворяет определенным условиям, чего, вероятно, изобретательные конструкторы смогут добиться (например, используя тот факт, что случайные ошибки встречаются в каждом из кубитов независимо друг от друга и что логические вентили выполнены достаточно точно), тогда квантовые компьютеры можно будет сделать нечувствительными к ошибкам. Они смогут надежно работать неограниченно долго.
За пределами традиционных математических знаний
История о "невозможных" логических схемах иллюстрирует потрясающий факт в физике вычислений. Когда мы обретаем новые сведения о физической реальности, мы иногда уточняем наши знания и в области логики и математики. Квантовая механика преобразит эти области так же, как она преобразила физику и технику. Причина заключается в том, что хотя математические истины существуют независимо от физики, мы приобретаем знания о них, изучая физические явления, и что мы можем узнать, диктуют нам физические законы. Математическое доказательство — это последовательность логических операций. И что доказуемо, а что доказать невозможно, зависит оттого, какие логические операции (вроде "НЕ") позволяют нам вводить законы физики. Эти операции должны быть физически настолько простыми, чтобы без каких-либо дополнительных доказательств мы понимали, что именно означает выполнить их, и в основе этого понимания лежит наше знание физического мира. Расширив арсенал элементарных математических операций за счет включения таких, как квадратный корень из "НЕ", квантовая физика позволит математикам пробить головой барьер, который, как считалось ранее, существует в мире чистой абстракции. Они смогут увидеть и доказать истины, которые в противном случае оставались бы навсегда скрытыми.
Вероятнее всего, первым практическим применением универсального квантового компьютера будет не факторизация, а моделирование других квантовых систем — задача, которая требует экспоненциально быстро растущего времени у классических компьютеров
Например, предположим, что для получения ответа на какую-то нерешенную математическую головоломку необходимо найти простые множители какого-то очень большого целого числа N— настолько огромного, что даже если бы вся материя во Вселенной пошла на постройку классических компьютеров, которые непрерывно работали бы с момента рождения Вселенной, то они все равно не смогли бы выполнить эту работу. Квантовый же компьютер смог бы быстро справиться с такой задачей. И вот когда математики станут публиковать решение этой задачи, в самом начале они должны будут указать эти множители, которые они как будто вытащили из шляпы фокусника: "Вот два целых числа, произведение которых равно N". Никакой бумаги не хватило бы, чтобы подробно описать, каким образом они получили эти множители.
Подобным образом квантовый компьютер, вероятно, будет давать математикам необходимый ключ, который поможет им найти ответ на математическую головоломку. Без такого ключа, реально обеспечить который не смог бы ни один классический процесс, результат так никогда и не был бы известен. Часть математиков уже рассматривают свой предмет как эмпирическую науку, которая получает результаты не только с помощью строгих доказательств, но и путем экспериментов. Квантовая физика выводит этот подход на новый уровень и делает его обязательным.
За пределами плохой философии
Если квантовая механика разрешает новый тип вычислений, почему же физики так беспокоились, что эта теория ограничит научный прогресс? Ответ нужно искать во временах становления квантовой теории.
Эрвин Шредингер, открывший основополагающее уравнение квантовой теории, как-то предостерег слушавших его лекцию, сказав, что то, что он собирается им рассказать, может показаться безумным.
Расширив арсенал элементарных математических операций за счет включения таких, как квадратный корень из "НЕ", квантовая физика позволит математикам пробить головой барьер, который, как считалось ранее, существует в мире чистой абстракции
Он продолжил, объяснив, что когда его знаменитое уравнение описывает различные истории частицы, это "не альтернативные события, в действительности все события происходят одновременно". Известно, что и у выдающихся ученых тоже, бывало, ум заходил за разум, но нобелевский лауреат 1933 г., должно быть, высказался достаточно сдержанно: что уравнение, за которое он получил премию, было верным описанием этих фактов. Шредингер чувствовал необходимость оправдываться не потому, что абсурдно интерпретировал свое уравнение, а ровно наоборот.

Гравюра Фламмариона. Эта знаменитая гравюра по дереву XIX в. (изначально черно-белая) заключает в себе философский вопрос: ограничено ли наше знание или мы всегда можем пробить своей головой путь в непознанное?
Как могло такое до очевидности безобидное утверждение когда-то считаться нелепостью? Это произошло потому, что большинство физиков стали жертвой плохой философии: философских доктрин, которые активно препятствовали приобретению других знаний. Философия и фундаментальная физика настолько тесно связаны между собой — несмотря на многочисленные заявления с обеих сторон об обратном, — что когда основная часть философов в первые десятилетия XX в. вошла в крутое пике, она потащила за собой и часть физиков.
Виной всему были такие доктрины, как логический позитивизм ("Если что-то нельзя проверить экспериментально, то оно не имеет смысла"), инструментализм ("Если предсказания работают, зачем утруждать себя выяснением того, как они получены?") и философский релятивизм ("Объективно утверждения не могут быть истинными или ложными, а только узаконенными или отвергаемыми конкретной культурой"). Ущерб был нанесен тем, что все эти доктрины имели общего: они отрицают реализм, философскую позицию, основанную на здравом смысле, которая говорит, что физический мир существует и научные методы позволяют получать знания о нем.
Люди хотят понять окружающую нас действительность независимо от того, как громко они это отрицают. Мы наконец минуем воображаемые пределы, покориться которым учила нас когда-то плохая философия
Именно в такой философской атмосфере физик Нильс Бор создал оказавшую большое влияние интерпретацию квантовой теории, которая отрицала возможность говорить о явлениях как существующих объективно. Было запрещено спрашивать, какое значение имеют физические переменные до того, как они измерены (и таким образом пройдена половина пути к квантовым вычислениям). Физики, которые в силу своей профессии не могли не хотеть спрашивать, старались так и поступать. Большинство из них продолжали учить и своих студентов тому же. Было признано, что самая передовая теория в самой фундаментальной из наук открыто противоречит самому существованию истины, логическому объяснению и физической реальности.
Не все философы отвергали реализм. Бертран Рассел и Карл Поппер были заметными исключениями. Так же как и не все физики. Альберт Эйнштейн и Дэвид Бом выступали против этой тенденции, а Хью Эверетт (Hugh Everett) предположил, что на самом деле физические величины одновременно принимают более чем одно значение (точка зрения, которой мы сами придерживаемся). В целом, однако, философов не интересовала реальность, и хотя физики продолжали использовать квантовую механику для изучения других областей физики, исследования природы самих квантовых процессов зашли в тупик.
В течение последних двух десятилетий ситуация постепенно начала улучшаться, и именно физика вернула философию на правильные рельсы. Люди хотят понять окружающую нас действительность независимо оттого, как громко они это отрицают. Мы наконец минуем воображаемые пределы, покориться которым учила нас когда-то плохая философия.
А что если в результате будет доказана несостоятельность теории? Что если какие-то более глубокие ограничения помешают попыткам построить масштабируемый квантовый компьютер? Было бы невероятно интересно узнать, что произошло. Такой исход — безоговорочно самый желательный. Он не только привел бы к пересмотру наших фундаментальных знаний в физике; мы ожидали бы, что это выведет нас к еще более захватывающим методам вычислений. Потому что если что-то остановит квантовую механику, то мы будем ожидать появления будоражащей воображение новой что-бы-ни-остановило-квантовую-механику теории, за появлением которой последуют будоражащие воображение новые что-бы-ни-остановило-квантовые-компьютеры. Так или иначе, пределов знаниям и прогрессу не будет никогда.
Перевод: А.П. Кузнецов
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
- The Fabric of Reality: The Science of Parallel Universes—and Its Implications. David Deutsch. Penguin, 1998.
- The Physics of Quantum Information: Quantum Cryptography, Quantum Telepor-tation, Quantum Computation. Dirk Bouw-meester, Artur Ekert and Anton Zeilinger. Springer, 2000.
- Quanta, Ciphers and Computers. Artur Ekert in The New Physics. Edited by Gordon Fraser. Cambridge University Press, 2006.
- The Beginning of Infinity: Explanations That Transform the World. David Deutsch. Penguin, 2011.
- The Emergent Multiverse: Quantum Theory according to the Everett Interpretation. David Wallace. Oxford University Press, 2012.
Источник: журнал "В мире науки"
Нет комментариев.
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.