Теория возмущений в космологии
1.
Выразить в терминах физических и сопутствующих координат отклонение скорости расширения от хаббловского.
2.
Предположим, что невозмущённым состоянием является покоящийся газ, равномерно распределённый в пространстве. В линейном приближении найти уравнения для возмущений.
3.
Показать, что в случае стационарного невозмущённого решения возмущения экспоненциально зависят от времени.
4.
Рассмотреть зависящие от времени адиабатические возмущения и найти характерный масштаб неустойчивости (джинсовской неустойчивости).
5.
Используя результат предыдущей задачи, рассмотреть случаи:
-
длинноволновых
-
коротковолновых
возмущений. Рассмотреть предельный случай коротких волн ) .
.
6.
В рамках ньютоновского приближения, пренебрегая энтропийными возмущениями, составить уравнение для малых относительных флуктуаций плотности 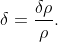
7.
Представить уравнение, полученное в предыдущей задаче, в виде уравнения для Фурье образа, исключив лагранжевы координаты. Найти порядок величины ''физической'' длины волны Джинса для Вселенной, в которой доминирует вещество.
8.
Найти зависимость флуктуаций плотности от времени для плоской Вселенной в случае доминирования
- материи,
- излучения.
9. Предположим, что частное решение дифференциального уравнения, полученного в задаче \ref{per6} имеет вид $\delta _1\left( t \right) \sim H\left( t \right).$ Построить общее решение для $\delta (t),$ рассмотреть случай плоской Вселенной, заполненной средой с уравнением состояния $p = w\rho.$
10. Показать, что поперечная или вращательная мода в расширяющейся Вселенной имеет тенденцию к уменьшению.
11. Исследовать квазистатический предел $(a = const,\,\dot a = 0)$ уравнения для малых флуктуаций плотности, полученного в задаче 6.
12. Показать, что квазистатическое приближение нельзя использовать для описания эволюции малых возмущений плотности в расширяющейся Вселенной.
13. Исследовать на устойчивость в линейном приближении, стационарную модель Вселенной, состоящей из материи $(p=0)$ и субстанции с уравнением состояния $p = w\rho.$
14. Построить корреляционную функцию для компонент Фурье относительных флуктуаций плотности, удовлетворяющую космологическому принципу.
15. Выразить корреляционную функцию относительных флуктуаций плотности через спектр мощности этих флуктуаций.
16. Неоднородность в распределении материи во Вселенной индуцирует возмущения метрики разного типа. В линейном приближении различные типы возмущений не взаимодействуют между собой (эволюционируют независимо). Выполнить классификацию возмущений.
17. Указать количество независимых функций, требуемых для описания возмущений, описанных в предыдущей задаче.
18. В первом порядке по малой величине $h_{ik}$ вычислить компоненты тензора энергии-импульса для Вселенной, заполненной идеальной жидкостью с уравнением состояния $p=w\rho$ и метрикой
$$ds^2=dt^2-a^2(t)(\delta_{ik}-h_{ik})dx^idx^k\;(i,k=1,2,3).$$
19. Найти в линейном приближении преобразование метрического тензора $g_{\mu\nu}$, генерируемое преобразованием координат вида $x^\alpha\rightarrow \tilde{x}^\alpha=x^\alpha+\xi^\alpha$, где $\xi^\alpha$ - бесконечно малая скалярная функция.
20. Используя результаты предыдущей задачи, найти возмущение метрики, генерируемое преобразованием вида $x^\alpha\rightarrow
\tilde{x}^\alpha=x^\alpha+\xi^\alpha$, где 4-вектор $\xi^\alpha=(\xi^0,\xi^i)$ удовлетворяет условию $\xi^i=\xi^i_\bot+\zeta^i$, $\xi^i_\bot$ -- 3-вектор с нулевой дивергенцией ($\xi^i_{\bot,i}=0$), $\zeta^i$ -- скалярная функция.