Показано, что тёмная энергия это естественный результат связи и теплового равновесия между между материей и фоном физического вакуума. Развивая это направление, было вычислено отношение плотностью тёмной энергии и суммой плотностей тёмной и барионной материи. Без подгонки параметров это отношение составляет $2.36$, что находится в прекрасном соответствии с результатом $7/3$, полученным из астрономических наблюдений. Эта работа не только подтверждает результаты наших прошлых рассчетов но и даёт простое объяснение загадочным свойствам тёмной материи.

Пионерские работы Джакобсона и Верлинде предложили новый подход к пониманию основ закона гравитации Ньютона. Основным результатом этих исследований стал вывод о возможной глубокой связи между законами термодинамики гидродинамики, гравитация (возможно) перестала быть универсальным взаимодействием и может быть объяснена с помощью микроскопической теории.

Согласно эффекту Унру, ускорение с которым движется наблюдатель, определяет температуру фона (вакуума) окружающего пространства, согласно формуле Унру $\left\vert \mathbf{a}\right\vert=2\pi k_{B}cT/\hbar .$

Для того чтобы обобщить эту формулу не для абсолютной величины ускорения, а для векторного поля, кажется очевидным следующее обобщение этой формулы $$ \mathbf{a}\left( \mathbf{R}\right) \mathbf{=}\frac{2\pi k_{B}c}{\hbar }\sum_{j=1}^{N}T_{j}\left( \mathbf{R}\right) \frac{\nabla _{\mathbf{R}}T_{j}\left( \mathbf{R}\right) }{\left\vert \nabla _{\mathbf{R}}T_{j}\left( \mathbf{R}\right) \right\vert }. $$

Здесь $T_{j}\left( \mathbf{R}\right) $ - поле распределения температуры для $j-$ частицы.

Очевидно, что направление этого ускорения увеличивается в направлении увеличения температуры, что находится в согласии с тепловым равновесием, описываемое свободной энергией $F_{fe}=U-TS.$

В статье предполагается, что $T_{j}\left( \mathbf{R}\right) $ имеет вид. $$ T_{j}\left( \mathbf{R}\right) =\frac{\hbar Gm_{j}}{2\pi k_{B}c}\left\vert \int d^{3}\mathbf{x}\phi _{j}^{\ast }\left( \mathbf{x},t\right) \frac{\mathbf{x}-\mathbf{R}}{\left\vert \mathbf{x}-\mathbf{R}\right\vert ^{3}}\phi _{j}\left( \mathbf{x},t\right) \right\vert , $$

где $m_{j}$ масса $j-$ частицы, $k_{B}$ постоянная Больцмана, а $c - $ скорость света.

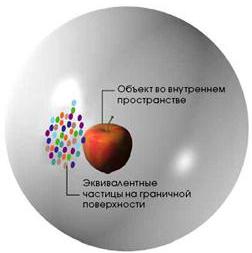
Далее в работе предполагается, что волновые функции частиц, находящихся в сферическом объёме радиуса $R_{s}$, имеют волновую функцию вида $\left\vert \phi _{j}\left( \mathbf{x},t\right) \right\vert =1/\sqrt{4\pi R_{s}^{3}/3}$ внутри области, и $\left\vert \phi _{j}\left( \mathbf{x},t\right) \right\vert =0$ везде вне её, как изображено на рисунке.

Изображено поле ускорения для области пространства, с квантовыми частицами находящимися внутри сферы, схематически изображенной красной пунктирной линией.

Исходя из приведенных выше соотношений, поле ускорения для классических частиц вне сферы и квантовых частиц внутри, имеет вид \begin{eqnarray} \mathbf{a}\left( \mathbf{R}\right) &=&\frac{4\pi }{3}Gn\mathbf{R},R=\left\vert \mathbf{R}\right\vert < R_{s}, \notag \\ \mathbf{a}\left( \mathbf{R}\right) &=&-\frac{G\Sigma _{j}m_{j}}{R^{3}} \mathbf{R},R=\left\vert \mathbf{R}\right\vert >R_{s}. \end{eqnarray} где $n=N/\sqrt{4\pi R_{s}^{3}/3}$ средняя плотность частиц, внутри сферы.

Далее, авторы рассматривают видимую часть Вселенной, с радиусом $R_{u}$, и общей, обнородно и изотропно распределённой плотностью тёмной и обычной (барионной) материи $n_{m}$. Скорость распределения вещества, принимается хаббловской $v\left( R\right) =Rc/R_{u}$.

После чего, делается преобразование Лоренца, для вещества, находящегося на расстоянии $R_{u}$ от наблюдателя \begin{equation} \varepsilon _{m}^{2}\left( R\right) =n_{m}^{2}c^{4}+\frac{n_{m}^{2}c^{4}R^{2}/R_{u}^{2}}{1-R^{2}/R_{u}^{2}}. \end{equation}

После чего делается стандартное для голографической физики предположение, ограничивающее энтропию системы, и находится соотношение для отношения плотностей тёмной энергии и тёмной материи. \begin{equation} \frac{\overline{n}_{v}}{n_{m}}=3\int_{0}^{1}y^{2}\sqrt{1+\frac{y^{2}}{1-y^{2}}}dy\approx 2.356. \end{equation}

Таким образом, если не обращать внимание на несколько непонятном выборе вида волновых функций, то этот тезультат получен только из голографического принципа в интерпретации Верлинде и хорошо известного хаббловского распределения скоростей.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.