Идея спонтанного нарушения симметрии часто наглядно иллюстрируется на примере явления ферромагнетизма. Представим себе сплошной шар из железа. Его атомы можно представить себе как маленькие магнитики, которые, вследствие действующих на них сил, выстраиваются параллельно своим соседям с одной и той же ориентацией север-юг.

При  достаточно высокой температуре, а именно некотором критическом значении  $770 {}^oC ~(1043 {}^oK) $ ,  энергетическое тепловое возбуждение атомов пересиливает эту тенденцию к выстраиванию магнитиков, и материал не проявляет склонности становиться магнитом в   макроскопическом масштабе, поскольку маленькие атомные магнитики оказываются ориентированными случайным образом. Однако при температуре ниже $770 {}^oC$ (так называемой «точки Кюри») энергетически более выгодна упорядоченная ориентация атомов, так что в идеальной  ситуации железо оказывается намагниченным. (Все же следует помнить, что здесь имеет место существенная идеализация куска реального железа, в котором детальное действие сил может иметь очень сложный характер. Хотя в достаточно малых областях внутри куска железа  описанная тенденция к намагничиванию может служить хорошим приближением, на практике такие намагниченные области стремятся ориентироваться случайным образом, так что кусок железа в целом не становится эффективным магнитом. Более того, чтобы железо стало  намагниченным в существенной степени, охлаждение ниже точки Кюри должно быть крайне медленным, и такой идеальной ситуации достигнуть непросто. В нашем теоретическом   обсуждении целесообразно пренебречь этими усложнениями и принять описанную идеализацию.)

Предположим теперь, что наш железный шар первоначально нагрет выше $770 {}^oC$ (но не настолько, чтобы он расплавился), так что вначале он не намагничен. Затем    окружающую среду постепенно охлаждают до температуры ниже критической $770 {}^oC$. Что при этом происходит? Естественно, что шар будет переходить в состояние с минимальной энергией, отдавая энергию внутренних колебаний атомов в более холодную окружающую среду. Из-за взаимодействия между соседними атомами минимальная энергия получается, когда все атомы выстроены в одном и том же направлении, так что шар становится намагниченным с определенным направлением полярности север-юг. Однако никакое из этих направлений не имеет предпочтения перед любым другим. Имеет место так называемое вырождение   состояний с минимальной энергией. Если нет выделенного направления в начальном нагретом ненамагниченном состоянии, то и направление конечной  намагниченности оказывается случайным. Это есть пример спонтанного нарушения симметрии: начальное сферически симметричное состояние переходит в состояние с более низкой симметрией, а именно с симметрией вращения вокруг результирующей магнитной оси север-юг. Состояние с симметрией $SO(3)$ (исходный горячий ненамагниченный шар) превращается в состояние с симметрией $SO(2)$ (холодный намагниченный шар).

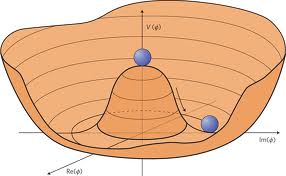
Ситуацию такого рода можно описать с помощью потенциала в форме мексиканской шляпы, изображенного на рис. 28.1. «Шляпа» представляет семейство допустимых  состояний системы (при нулевой температуре окружающей среды), а «высота» - энергию системы.

Мы видим, что существует равновесное состояние (имеющее горизонтальную касательную плоскость), соответствующее вершине шляпы, которое обладает полной симметрией  исходной группы; на рисунке эта группа представлена вращением вокруг вертикальной оси.  (Вращательная симметрия $SO(2)$ является аналогом полной симметрии железного шара $SO(3)$), нам пришлось отбросить одно пространственное измерение, чтобы получить наглядную  картину. Вершина шляпы представляет полное отсутствие намагниченности шара как целого.)

Однако такое равновесие, представляющее ненамагниченное состояние, неустойчиво и не соответствует минимуму допустимых энергий. Таким минимумам отвечают состояния,   представленные горизонтальными частями (по всей окружности) на полях шляпы (различным точкам на полях соответствуют различные направления полной намагниченности железного шара). 

Исходное состояние на вершине можно рассматривать как состояние находящегося там шарика, представляющего физическое состояние, оставшееся от предшествующего  высокотемпературного состояния. Потеря устойчивости означает, что шарик скатится из этой точки вниз (предполагается наличие влияния некоторого случайного возмущения) и займет состояние покоя в некоторой точке на полях шляпы. Каждая точка на полях, в которой  может оказаться шарик, представляет некоторое направление намагниченности, которую может приобрести в конечном счете наш железный шар. Положение шарика представляет конечное физическое состояние. Однако в силу вращательного вырождения для шарика нет  предпочтительного места, в котором он в конце концов окажется. Все положения равновесия на полях шляпы одинаково хороши. Выбор шарика есть дело случая, и коль скоро такой выбор сделан, происходит нарушение симметрии из-за появления некоторого случайно выбранного направления.

Рис. 28.1. Спонтанное нарушение симметрии в системе с потенциалом в форме  мексиканской шляпы, определяющим допустимые состояния; мерой энергии служит высота. Состояние системы  представлено шариком, движение которого ограничено поверхностью шляпы. Если температура окружающей среды достаточно высока (точка Кюри), равновесное состояние системы представляется шариком, покоящимся на вершине шляпы, оно обладает полной вращательной симметрией (в данной  упрощенной картине симметрией $SO(2)$). При понижении температуры шарик скатывается вниз и достигает в конечном счете некоторой произвольной точки равновесия на полях шляпы, что нарушает полную вращательную симметрию. 

Явление такого рода, когда понижение окружающей температуры приводит к резкому кардинальному изменению природы устойчивого равновесного состояния вещества,  называется фазовым переходом. В нашем примере с железным шаром фазовый переход происходит, когда шар из ненамагниченного состояния (при температуре выше $770 {}^oC$) переходит в   однородно намагниченное состояние (при температуре ниже $770 {}^oC$). Более известны явление замерзания (переход из жидкого состояния в твердое при понижении температуры) и  обратный процесс кипения (превращение жидкости в пар при повышении температуры). Фазовый переход при понижении температуры часто сопровождается понижением симметрии, но это не так существенно. 

В КТП фазовый переход часто описывается как выбор нового вакуумного состояния (вроде $| \Theta  \rangle $) , когда состояние «туннелирует» (квантово-механическое туннелирование имеет место, когда квантовая система  самопроизвольно переходит из одного состояния в другое состояние с более низкой энергией (с  излучением избытка энергии) при наличии энергетического барьера, препятствующего такому переходу в классической физике)  из одного вакуума в другой. Такое описание следует рассматривать как некоторое приближение, однако, строго говоря, не  существует (унитарного) квантово-механического процесса, который переводит состояние из одного сектора в другой (под «сектором» понимаются состояния, которые можно построить при данном выборе вакуумного состояния $| \Theta  \rangle $); состояния различных секторов принадлежат различным гильбертовым пространствам. Приближение, в котором система предполагается бесконечной, хотя на самом деле она конечна, в практических   ситуациях вполне приемлемо. Например, таким образом трактуется хорошо известное явление сверхпроводимости (падение электрического сопротивления до нуля при достаточно низкой температуре): сверхпроводимость рассматривается как фазовый переход, сопровождающий понижение симметрии, нарушающее обычную $U(1)$ симметрию электромагнетизма. 

В частном примере, представленном на рис. 28.1, симметрия понижается от группы вращений вокруг оси $SO(2)$ до тривиальной группы $SO(1)$, содержащей всего один элемент (так что в данном примере в конечном счете теряется вся симметрия, поскольку конечное положение шарика полностью нарушает симметрию) (на отсутствие в этом примере симметрии относительно отражения указывает буква S в  обозначении $SO(2)$). Однако аналоги этой «шляпы» с более высокой размерностью иллюстрируют спонтанное понижение симметрии от $SO(p)$ до $SO(p-1) c p>2.$ (Наш железный шар иллюстрирует случай $p=3.$) Можно также использовать картину с «мексиканской шляпой» для иллюстрации понижения симметрии от $U(2)$ до $U(l),$ что имеет место в стандартной модели физики элементарных частиц, где электрослабая симметрия $U(2)$ понижается до симметрии  электромагнетизма $U(l)$ при температуре $10^{16} K,$ которую имела Вселенная через $10^{-12}c $ после Большого взрыва. В более общих теориях Великого объединения фигурируют другие  группы, например $SO(5),$ так что можно рассматривать разные стадии нарушения симметрии при различных температурах. Так, при некоторой температуре, намного большей $10^{16} K$ (т.е. значительно раньше, чем через $10^{-12}c $  после Большого взрыва), симметрия $SO(5)$    может нарушиться с понижением до некоторой подходящейt  симметрии, которая содержит группу  $SO(3) $    для сильного взаимодействия и $SU(2)\times U(1) /Z_2 $  (т. е. $SO(2) $) для электрослабого взаимодействия.

Космические топологические дефекты

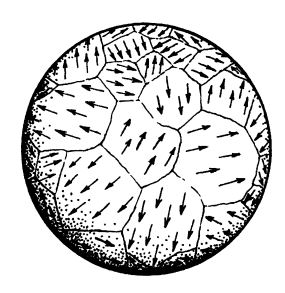
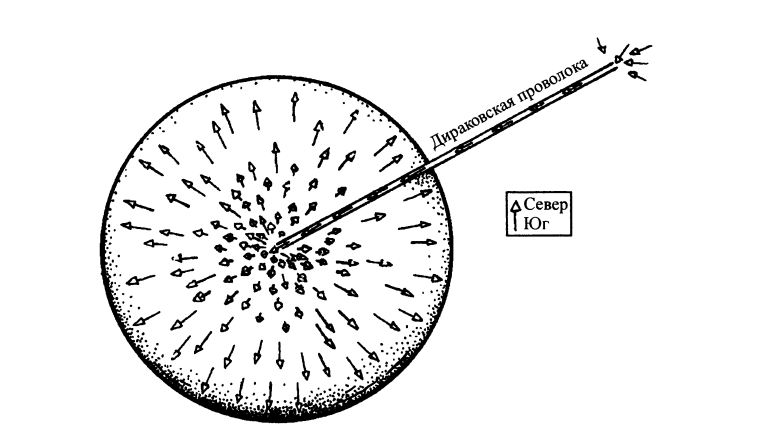
Мы должны, однако, иметь в виду, что такое  нарушение симметрии редко происходит «сразу повсюду», вместо этого появляются домены — области, в которых симметрия нарушается в различных «направлениях». Рассмотрим снова наш идеализированный железный шар. Можно  ожидать, что случайный начальный выбор направления  намагниченности будет различным в разных местах шара.  Если охлаждение происходит достаточно медленно, то эти неоднородности «сглаживаются», и получается однородный магнит. Однако при быстром охлаждении может оказаться, что мы получим «лоскутную» структуру с   различным направлением намагниченности, подобную   показанной на рис. 28.2. Размер образующихся ячеек и  составляемая ими картина, помимо всего прочего, могут зависеть от скорости охлаждения. Они зависят также от того, какова «связь» между различными областями и в какой мере направление намагниченности в одной области шара может «переключаться» под влиянием соседних областей. Более серьезным и интересным явлением оказывается возникновение топологических дефектов, которые нельзя устранить никаким поворотом направлений намагниченности внутри шара. Таким дефектом является «магнитный монополь Дирака» (изолированный северный или южный магнитный полюс). Такой монополь невозможно создать в обычном пространстве никаким набором магнитов и  токов. Можно, однако, получить эффективный монополь, позволив магнитному заряду течь вдоль «дираковской проволоки», как показано на рис. 28.3. Если ввести магнитные заряды в теорию Максвелла, то «проволока» появится только в потенциале A и ее можно будет устранить, приняв подходящую «расслоенную» точку зрения. Монополь такого рода может существовать также в некоторых неабелевых калибровочных теориях.  

Рис. 28.2. В идеальном случае, при медленном охлаждении  ферромагнетика ниже точки Кюри,  векторы намагниченности  составляющих его атомов выстраиваются в одном и том же (произвольном) направлении. Однако на практике (или при слишком быстром охлаждении) мы получаем «лоскутную структуру» с различными  направлениями намагниченности.

Усложнения в картине спонтанного понижения симметрии, частично продемонстрированные на «земном» примере железного шара, относятся также и к фундаментальным  физическим теориям более возвышенного уровня (например, к теории электрослабого  взаимодействия или теории Великого объединения), в самой основе которых лежит идея спонтанного нарушения симметрии. Можно ожидать возникновения топологических дефектов в большом (космологическом) масштабе, если такое спонтанное нарушение симметрии имело место в ранней Вселенной. В общем случае (применительно к трехмерному пространству)  существуют три основных вида топологических дефектов в зависимости от размерности той области, в которой они проявляются. Они носят название (космических) монополей (нулевая пространственная размерность), космических струн (одно пространственное измерение) и  доменных стенок (два пространственных измерения). Размерность зависит от топологических особенностей, совместимых с соответствующей группой симметрии. Важной особенностью топологических дефектов является невозможность их устранения путем непрерывных  изменений «направления» нарушения симметрии (при этом мы считаем, что в самом дефекте отсутствует определенное направление нарушения симметрии, тогда как в других местах имеют место непрерывные изменения этого направления).  Следует иметь в виду, что   понятие «направления» означает не направление в обычном пространстве, а более абстрактное «направление», относящееся к рассматриваемой физической модели (например, в теории электрослабого взаимодействия оно определяет меру смешивания электронов с нейтрино).

Рис. 28.3. Магнитный монополь может возникнуть, если каким-то образом «накачать» в центр сферы избыточный «южный полюс» по «магнитной проволоке». Если допустить существование магнитных источников в теории Максвелла, такой полюс можно ввести в центр, и тогда дираковская «проволока» нужна лишь для создания сбоя потенциала А. Этот сбой можно устранить, приняв «расслоенную» точку зрения (такие монополи появляются также в некоторых неабелевых калибровочных теориях)

В геометрическом смысле можно было бы говорить о векторном расслоении во всем   пространстве-времени. Топологические соображения по-прежнему применимы, и топологические дефекты представляют серьезные проблемы, от которых нельзя отмахнуться, если нарушение симметрии включается в фундаментальную физическую теорию в качестве составной части.

Действительно, космические струны огромного масштаба (превышающего даже  галактические масштабы) рассматриваются как существенный фактор, определяющий  возникновение в исходном газе тех неоднородностей, которые привели к образованию галактик.

Гравитационное поле такой космической струны можно рассматривать как результат   применения «метода ножниц и клея» к пространству-времени Минковского. Оперируя  пространственными терминами, можно представить себе «сектор», удаленный из 3-пространства, который ограничен парой полуплоскостей, образующих двугранный угол $\alpha, $ ребром которого служит сама струна (рис. 28.4). Чтобы построить геометрию космической струны, следует снова «склеить» вместе две плоские поверхности. (В предложенных моделях угол $\alpha, $ составляет $10^{-6}.$)

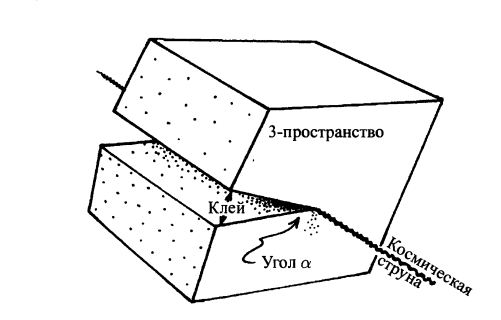
Рис. 28.4. Гравитационное поле космической струны можно построить, применяя к 4-пространству Минковского «метод ножниц и клея». В 3-пространстве удаляется сектор, ограниченный двумя  полуплоскостями, образующими двугранный угол $\alpha, $, ребром которого служит струна. Поверхности полуплоскостей затем склеиваются.

Читателю может не без основания показаться, что это слишком крайние меры для создания такого «банального» объекта, как обычная галактика. Но в вопросе о происхождении галактик пока имеются теоретические загадки, и потому не стоит отметать с порога подобные экзотические идеи, несмотря на их, казалось бы, неправдоподобный вид. 

Действительно, одна из наиболее притягательных моделей формирования галактик, получившая некоторое подтверждение со стороны результатов наблюдений, предполагает, что их  «зародышами» послужили сверхмассивные черные дыры, ныне находящиеся в их центрах.

Но черные дыры сегодня следует считать не экзотикой, а стандартными физическими  объектами! Большинство таких предполагаемых топологических дефектов относится к теориям  (например, различным теориям Великого объединения), которые пока не имеют существенной однозначной поддержки со стороны наблюдений. С другой стороны, теория электрослабого взаимодействия очень хорошо подтверждается наблюдениями, поэтому следует отнестись со вниманием к результатам применения этой теории к процессам в ранней Вселенной.

Космические монополя, возникающие в результате нарушения симметрии электрослабого взаимодействия, с топологической точки зрения возможны, но не являются необходимыми.

Они могут возникать при спонтанном понижении симметрии от $U(1)$ до $U(2)$, но лишь при условии, что в ненарушенной фазе с $U(2)$-симметрией, которая предполагается  существовавшей до момента $10^{-12}$ с, уже присутствуют так называемые «калибровочные монополи».

Такие монополи могут возникать при более раннем нарушении более высокой симметрии теории Великого объединения, но эти идеи никоим образом не являются необходимой  составной частью теории электрослабого взаимодействия!

Подобные «калибровочные монополи» являются, в рамках (неабелевой) теории Янга-Миллса, аналогом «магнитных монополей», впервые предложенных Дираком (в 1931 году) в рамках (абелевой калибровочной) теории электромагнетизма. Путем остроумных рассуждений Дирак показал, что даже если бы в природе существовал одиночный  магнитный монополь (отдельный северный или южный магнитный полюс), то все электрические заряды должны были бы иметь значения, кратные некоторой величине, обратно пропорциональной магнитной силе монополя. Фактически современные наблюдения убедительно свидетельствуют, что все электрические заряды действительно кратны некоторому  определенному значению (например, заряду анти-d-кварка, составляющему одну треть заряда протона. Это можно было бы счесть косвенным подтверждением  существования магнитных монополей. Тем не менее чтобы такие монополи не оказались в резком  конфликте с наблюдениями, они должны обладать совершенно необычными свойствами! (В противном случае они создавали бы эффект «закорачивания» космических магнитных полей, тогда как такие поля наблюдаются в просторах Вселенной.) Аналогично монополи Янга-Миллса должны были бы вступать в конфликт с наблюдениями, если бы они  присутствовали в современной Вселенной в достаточном количестве. Как мы скоро увидим, это понятие играет весьма важную роль в развитии космологии! 

Проблемы с нарушением симметрии в ранней Вселенной

Прежде чем перейти к этому, полезно вернуться к нарушению симметрии в теории электрослабого взаимодействия, которое, как предполагается, имело место через $10^{-12}$ с после Большого взрыва. Должны ли мы относиться к этому как к реальному явлению или это всего лишь артефакт данного способа изложения теории? Насколько я могу судить, большинство теоретиков в области электрослабого взаимодействия склонно рассматривать этот процесс как реальный. Тем самым я предупреждаю читателя, что в вопросе о реальности этого явления я занимаю не вполне стандартную позицию. Тем не менее двинемся дальше и рассмотрим некоторые трудности, связанные с идеей нарушения симметрии.

Предположим, что, вопреки моему собственному (нестандартному) взгляду на этот предмет, в ранней истории Вселенной существовал период (предшествующий моменту  времени $10^{-12}$ с после Большого взрыва), когда сохранялась точная симметрия $U(2)$) и все лептоны и кварки имели одинаковую массу, так что электроны и нейтрино можно было рассматривать на равных основаниях, a W- и Z-бозоны и фотон путем подходящего   «поворота» переводить друг в друга в соответствии с $U(20)$-симметрией. Затем, в момент времени $10^{-12}$ с, температура всюду во Вселенной упала чуть ниже критического значения.

В этот момент был сделан случайный выбор $(W^-,W^+, Z^0, \gamma)$ из полного $U(2)$-симметричного многообразия $\mathcal{G}$ возможных наборов калибровочных бозонов. Мы не ожидаем, что это произошло совершенно однородным образом во всем пространстве, одновременно во всей Вселенной. Мы предполагаем, что, как и в случае доменов намагниченности железного шара, показанных на рис. 28.2, в некоторых областях будет реализован один из возможных вариантов выбора, а в других местах — другой.

Здесь следует обратиться к вопросу, как понимать в данном контексте слова «тот же  самый» (одинаковый, такой же) и «другой». До момента понижения симметрии пространство $\mathcal{G}$ возможных калибровочных бозонов в каждой точке пространства-времени обладает полной симметрией $U(2)$. В понятии расслоения заложено, что не существует предпочтительного способа установления тождества между пространством $\mathcal{G}$  в одной точке и в какой-то другой точке. Таким образом, у нас нет априорного правила, определяющего, какой элемент  пространства $\mathcal{G}$  в одной точке следует считать «тем же самым» элементом, что и некоторый элемент пространства $\mathcal{G}$  в другой точке. Это, по-видимому, позволяет нам придерживаться той точки зрения, что мы можем просто определить понятие «тот же самый», отнеся его к тому определенному выбору, который делается при спонтанном нарушении симметрии.

Согласно такой точке зрения, тот выбор $(W^-,W^+, Z^0, \gamma)$ который «замораживается» в  одной точке, должен быть тождествен соответствующему выбору $(W^-,W^+, Z^0, \gamma)$ в любой другой точке, так что мы не можем говорить о каком-то «несоответствии» между  нарушениями симметрии в разных точках при возникновении доменов намагниченности железа, показанном на рис. 28.2.

Однако такая точка зрения сталкивается с общей идеей, лежащей в основе  калибровочной теории, согласно которой не только пространства $\mathcal{G}$   — слои расслоенного  пространства $\mathcal{Bg}$  с пространством-временем $\mathcal{M}$   в качестве базисного пространства, — но и конкретная калибровочная теория (в данном случае теория ненарушенного электрослабого  взаимодействия) определяются в терминах связности на этом расслоении. Эта связность определяет локальное отождествление (параллелизм) пространств $\mathcal{G}$   при перемещении вдоль некоторой замкнутой кривой в пространстве-времени $\mathcal{M}.$ В общем случае такая  идентификация не является глобально согласованной при обходе замкнутых петель (из-за   наличия кривизны связности, определяющей нетривиальное калибровочное поле. В любом случае случайный фактор, вносимый нарушением симметрии в различных точках, приводит к тому, что локальный параллелизм $\mathcal{G}$  -пространств в общем случае не согласуется с тем выбором, который делается при спонтанном нарушении симметрии, так что картина на рис. 28.2 может служить неплохой аналогией. Можно представить себе, что, как и в случае достаточно медленного охлаждения железного шара, неоднородности со временем будут «сглаживаться», если предположить отсутствие топологических дефектов вроде тех, что показаны на рис. 28.3 и 28.4. Вопрос, который я хочу задать, состоит в том, найдется ли «достаточно времени» в случае спонтанного нарушения симметрии электрослабого взаимодействия.

Такая проблема возникает в связи с горизонтом для частиц. Рассмотрим схематическую конформную диаграмму на рис. 28.5. 

Наблюдатель, находящийся в точке $p,$ видит квазары в двух противоположных направлениях, которым соответствуют пространственно-временные точки $q$ и $r.$ Согласно стандартным моделям FRW, при достаточно большом красном смещении квазаров световые конусы прошлого для точек $q$ и $r$ не будут пересекаться, так что  никакой связи между этими точками быть не может. Не имея связи между собой, они не будут иметь времени для согласованного «сглаживания» нарушений симметрии указанным образом. Вскоре мы рассмотрим «инфляционный сценарий», который отодвигает назад   линию Большого взрыва на конформной диаграмме, так что точки $q$ и $r$ в конечном счете оказываются связанными между собой. Но в данном случае это нам не поможет, поскольку 3-поверхность $\sum,$ на которой имеет место нарушение симметрии электрослабого  взаимодействия, эффективно играет роль Большого взрыва в этом нашем рассуждении, использующем соображения причинности, так как спонтанное нарушение симметрии предполагается  возникающим на 3-поверхности $\sum,$  случайным образом, без эффективного влияния обычных условий причинности.

Теперь прямые $qp$ и $rp$ представляют нулевые линии, поэтому только фотон может попасть из точки $q$ в точку $p$ или из $r$ в $r$, тогда как $W-$ или $Z-$бозоны этого сделать не в состоянии, поскольку фотон является единственным безмассовым членом семейства калибровочных бозонов. Таким образом, в отношении этих двух нулевых линий нам  необходимо иметь четкое представление о том, что есть фотон. Понятие «фотона» в точке $q$, скорее всего, не будет совпадать (в указанном выше смысле) с понятием «фотона» в точке $r,$ поскольку каждый из них, как предполагалось, выделялся случайным образом без  взаимного причинного влияния и при отсутствии достаточного времени для установления связи между ними . Могут ли фотоны «разного сорта» с течением времени «сглаживаться», чтобы избавить принимающего их наблюдателя в точке $p$ от возможного недоразумения, связанного с объединением $W-Z-\gamma ?$ Я не вижу, как это можно осуществить без  значительного отступления от прямой нулевой (т. е. «светоподобной») связи точек $q$ и $r$ с точкой $p$. Это может привести к резкому конфликту с тем фактом, что удаленные объекты можно наблюдать с помощью оптических телескопов. Мне представляется, что здесь заключена опасность несоответствия теории результатам наблюдений, хотя я не встречал обсуждения этой проблемы в литературе.

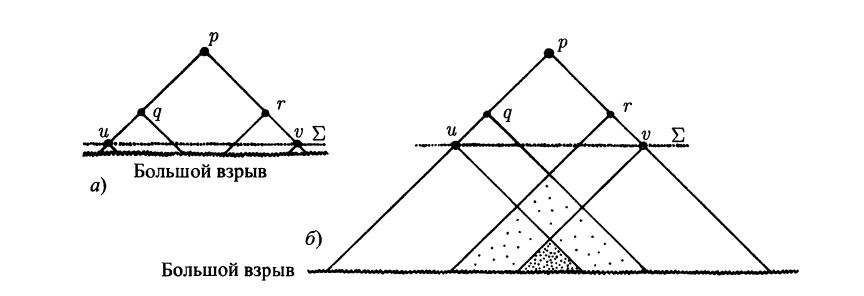
Рис. 28.5. Схематические конформные диаграммы, иллюстрирующие причинную (не)зависимость в ранней Вселенной, а) Наблюдатель, находящийся в точке р, видит квазары в противоположных направлениях (точки $q$ и $r$). Если пунктирная прямая представляет 3-поверхность $sum$ в момент  времени $10^{-12}c,$ когда предполагается нарушение симметрии электрослабого взаимодействия (связывавшей фотон $\gamma$ с $W-$ и $Z-$бозонами), то некоторый «замороженный» выбор фотона $\gamma$  в точке $q$ почти наверняка будет отличаться от выбора в точке $r$, поскольку пересечения конусов прошлого для этих точек с поверхностью $\sum$ разделены таким образом, что информация о совпадении или различии  выборов не может достигнуть точки $p.$ Аналогично, если поверхность $\sum$  представляет момент расцепления в момент времени $10^{13}$, температуры в точках $n$ и $v$ не могут быть выравнены в результате термализации из-за разделения соответствующих конусов прошлого, б) Инфляционное «решение» описанной «проблемы горизонта». Линия Большого взрыва отодвигается назад, так что конусы прошлого для точек $q$ и $r$ теперь пересекаются до достижения 3-поверхности Большого взрыва. Однако проблема остается нерешенной, поскольку пересечение конусов прошлого происходит до «замерзания» в момент времени  $10^{-12}.$

Некоторые читатели, несомненно, могут выразить недовольство (хотя, возможно, и не вслух) тем, что я как будто игнорирую все весьма впечатляющие подтверждения теории  электрослабого взаимодействия результатами наблюдений. Я вовсе не собираюсь отказываться от всего этого лишь из-за некоторых затруднений, связанных с явлениями  космологического масштаба! Отнюдь нет. Я никоим образом не предлагаю отказаться от прекрасных достижений теории электрослабого взаимодействия, однако предпочитаю занимать  позицию, несколько отличную от общепринятой, в отношении нарушения $U(2)$-симметрии этого взаимодействия. Насколько я понимаю, истинная схема, предложенная Природой в  отношении элементарных частиц, пока скрыта от нас. Такая схема должна быть математически согласованной и не должна иметь отрицательных черт нашей сегодняшней КТП, которая на многие разумно поставленные физические вопросы выдает ответ $'' \infty ''$ Каким образом эта (пока не известная) «правильная» теория даст ответы в виде конечных величин, мы пока не знаем. Поэтому мы прибегаем к разнообразным «трюкам», благодаря которым наш путь оказывается сотканным из исторического везения и исключительной человеческой   изобретательности, позволяя нам получать конечные результаты, согласующиеся с наблюдениями.

На нашем нынешнем уровне понимания нам определенно нужна перенормируемая теория, объединяющая слабое и электромагнитное взаимодействия, которая содержала бы не только идею нарушенной неабелевой калибровочной симметрии, указывающую способ построения перенормируемой теории, но и налагаемые при этом ограничения, которые подвели бы нас ближе к семейству глубоких истин в отношении того пути, на котором эти взаимодействия объединяются как часть некоторой более широкой картины. Но пока я не вижу, почему спонтанно нарушенная симметрия должна быть истинным путем Природы в мире элементарных частиц. На самом деле существуют и другие пути к пониманию того, как требование перенормируемости позволяет получить необходимые соотношения между параметрами теории электрослабого взаимодействия!

Это выдвигает важный вопрос: действительно ли понятие симметрии, столь широко представленное во многих идеях, направленных на  раскрытие тайн Природы, играет такую фундаментальную роль, какая ему обычно отводится?

Я не вижу, почему это всегда должно быть так. Я не убежден, что построение физики  элементарных частиц на основе некоторой большой группы симметрии (а именно это является составной частью философии Великого объединения) действительно дает «простую»  картину, коль скоро речь идет о фундаментальной физической теории. На мой взгляд, большие геометрические группы симметрии не упрощают, а усложняют картину. Вполне может быть, что законам природы присуща фундаментальная асимметрия, а та симметрия, которую мы наблюдаем, есть лишь приближенное свойство, которое не сохраняется на более глубоких уровнях.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.