Черные дыры: физика и астрофизика
Позвольте мне начать со старого персидского предания. Однажды бабочки организовали летнюю школу, посвященную великой тайне пламени. Обсуждались различные модели, но никто не мог убедительно объяснить загадку. Тогда одна смелая бабочка вызвалась на собственном опыте выяснить, что же такое огонь. Она полетела к ближайшему замку, приблизилась к окну и увидела горящую свечу. Она вернулась, взволнованная, и рассказала о том, что видела. Но мудрая бабочка, бывшая председателем конференции, сказала, что информации не стало больше, чем было ранее.
Загадка черных дыр
Затем вторая бабочка отправилась к замку, влетела в окно и коснулась огня своими крылышками. С большим трудом вернувшись, она рассказала свою историю, но вновь мудрый председатель сказал: "ваше объяснение более неудовлетворительно". И третья бабочка отправилась туда же, врезалась в свечу и сгорела. Наблюдавший за этим мудрый председатель тогда изрек: "Ну что ж, наш коллега узнал все об огне. Но это знание потеряно для нас вместе с ним..."
Как вы можете догадаться, эта история легко переносится с бабочек на ученых, занимающихся загадкой черных дыр. Некоторые астрономы, вооружившись мощными инструментами, такими, как космические телескопы, проводят косвенные наблюдения очень далеких черных дыр; как первая бабочка, они признают их существование, но способны получить совсем немного информации о их природе. Теоретики пытаются постичь эту загадку с помощью общей теории относительности, квантовой механики и высшей математики; как вторая бабочка, они получают чуть больше информации, но немногим больше, чем первые. Наконец, третьей бабочке мог бы соответствовать космонавт, направляющийся прямиком в черную дыру, но в конце концов он не смог бы рассказать о том, что узнал. Однако, с помощью численного моделирования, вроде проводившегося в Обсерватории Медон (Observatoire de Meudon), о котором я расскажу ниже, находящиеся снаружи черной дыры могут получить некоторое представление о том, что происходит внутри.
Физика черных дыр
Плененный свет
Давайте поставим себя на место второй бабочки и рассмотрим черную дыру с точки зрения теоретической физики. Согласно простейшему определению, черная дыра - это область пространства-времени, в которой гравитационный потенциал $GM/R$ превосходит квадрат скорости света $c^2$. Преимуществом такого определения является независимость его от конкретной теории гравитации. Оно может быть использовано в рамках теории Ньютона. Из него также следует более известное определение, согласно которому черной дырой являются астрономические объекты со скоростью убегания, превышающей скорость света.В действительности идея подобных объектов имеет более чем двухвековую историю. В журнале Philosophical Transactions of the Royal Society (1784), Джон Митчелл (John Michell) заметил, что "если бы радиус шара той же плотности, что и у Солнца, превзошел солнечный в 500 раз, (...) весь излученный таким телом свет должен был бы к нему вернуться", и, независимо, в 1796 Пьер Симон Лаплас (Pierre-Simon de Laplace) писал в работе Exposition du Systeme du Monde: "Un astre lumineux de meme densiteque la terre et dont le diametre serait deux cents cinquante fois plus grand que celui du soleil, ne laisserait, en vertu de son attraction, parvenir aucun de ses rayons jusqua nous ; il est donc possible que les plus grands corps lumineux de l'univers soient, par cela meme, invisibles". Поскольку в то время люди еще не могли представить себе плотностей существенно больших, чем у обычного вещества, размеры и масса таких "невидимых тел" получались огромными - порядка $10^7$ масс Солнца, что соответствует современным "сверхмассивным" черным дырам. Тем не менее, в расчетах, проведенных Митчеллом и Лапласом, узнается широко известная формула для критического радиуса тела массы $M$.
$$ R_S = {2 GM\over c^2} \approx 3 {M\over M_{\odot}} км, $$где $M_{\odot}$ - масса Солнца. Любое сферическое тело массы $M$, заключенное внутри критического радиуса $R_{S}$, должно быть черной дырой.
Эти рассуждения были быстро забыты, главным образом из-за развития волновой теории света, в рамках которой вообще не было сделано ни одной оценки влияния гравитационного поля на распространение света. И только общая теория относительности, релятивистская теории тяготения, в рамках которой свет полностью подчинен гравитации, привела к появлению новых идей и гораздо более глубокому пониманию черных дыр.
Для наглядного описания черных дыр в пространстве-времени я буду использовать понятие светового конуса. Напомню, что это такое. На рисунке 1 световой импульс излучается в заданной точке пространства. Волновой фронт - это сфера, расширяющаяся со скоростью $c = 300\;000$ км/с. Он изображен на рис. a) в три разных момента времени. Представленный же на рис. b) световой цилиндр отражает полную историю волнового фронта на одной пространственно-временной диаграмме. При удалении одного пространственного измерения сферы становятся окружностями. Расширяющиеся световые окружности образуют конус с вершиной в источнике излучения. Если на этой диаграмме мы примем за единицу длины $300 000$ км, а времени - $1$ секунду, все световые лучи будут распространяться под углом $45^{\circ}$.
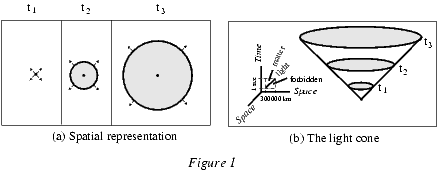
Рисунок 1. Световой цилиндр.
Световой конус позволяет нам изобразить причинную структуру любого пространства-времени. Возьмем для примера плоское пространство-время Минковского, используемое в специальной теории относительности (рисунок 2). Для любого события $E$ световые лучи образуют два конуса. Лучи, излученные в $E$, дают световой конус будущего, принятые в $E$ - прошлого. Физические частицы не могут двигаться быстрее света: их траектории должны оставаться внутри этих двух световых конусов.
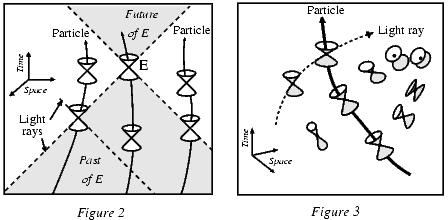
Рисунки 2 и 3. Пространственно-временной континуум специальной теории относительности и "гибкое" пространство-время общей теории относительности.
Ни один луч света или частица, прошедшие через точку $E$, не способны выйти за пределы, ограниченные световыми конусами. Инвариантность скорости света в вакууме отражает тот факт, что все конусы имеют один и тот же наклон. Это является следствием того, что пространственно-временной континуум специальной теории относительности, в котором отсутствует гравитирующее вещество, является плоским и "жестким". Как только появляется гравитация, пространство-время искривляется и в игру вступает общая теория относительности.
Так как Принцип Эквивалентности постулирует влияние гравитации на все виды энергии, световые конусы искривляются вслед за пространственно-временным континуумом (рисунок 3). Однако, специальная теория относительности остается локально справедливой: мировые линии частиц остаются связанными со световыми конусами, даже когда последние сильно наклоняются и деформируются гравитацией.
Сферически-симметричный коллапс
Теперь проанализируем причинную структуру пространства-времени вокруг звезды, коллапсирующей под действием гравитации звезды - именно этот процесс, как считается, приводит к образованию черных дыр.
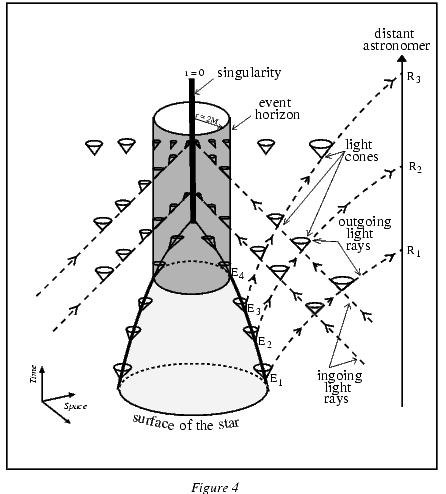
Рисунок 4. Пространственно-временная диаграмма, иллюстрирующая образование черной дыры в процессе гравитационного коллапса.
Рисунок 4 отражает полную историю коллапса сферически-симметричной звезды, от начального сжатия до формирования черной дыры и сингулярности.
Оси двух пространственных измерений горизонтальны, ось времени вертикальна и направлена вверх. Центру звезды соответствует $r=0$. Кривизна пространства-времени изображена с помощью световых конусов, образуемых траекториями фотонов. Вдали от гравитирующего центра кривизна настолько мала, что световые конусы являются прямыми. В более сильном поле из-за кривизны конусы деформированы и наклонены внутрь. На критической поверхности радиуса $r=2M$ конусы повернуты на $45^{\circ}$ и одна из их образующих становится вертикальной, так что все разрешенные траектории движения частиц и электромагнитных волн направлены внутрь. Это так называемый горизонт событий, граница черной дыры (серая область на рисунке). Внутри вещество продолжает коллапсировать в сингулярность нулевого объема и бесконечной плотности на $r=0$. Как только черная дыра сформировалась и все вещество исчезло в сингулярности, геометрия пространства-времени сама по себе продолжает коллапсировать к сингулярности, как показано с помощью световых конусов.
Испускание световых лучей в точках $E_1, E_2, E_3$ и $E_4$ и их прием удаленным астрономом в $R_1, R_2, R_3, ...$ наглядно иллюстрирует разницу между собственным временем, измеряемым часами, покоящимися на поверхности звезды, и истинным временем, измеряемым удаленным независимым наблюдателем. Интервалы собственного времени между четырьмя моментами испускания света равны. Однако, соответствующие интервалы между моментами приема сигналов становятся все больше и больше. В пределе, сигналы, испущенные в $E_4$, при формировании горизонта, достигают удаленного наблюдателя за бесконечное время. Это явление "остановки времени" - иллюстрация его чрезвычайной гибкости, предсказанной общей теорией относительности Эйнштейна, согласно которой время течет по-разному для двух ускоренных друг относительно друга наблюдателей - или, согласно Принципу Эквивалентности, находящихся в точках с различными гравитационными потенциалами. Поразительным следствием является то, что любому внешнему астроному никогда не удастся увидеть формирование черной дыры.
Рисунок 5 образно иллюстрирует эффект остановки времени. Задачей космического корабля является исследование внутренности черной дыры - желательно сверхмассивной, так чтобы он не был разрушен слишком рано приливными силами. На борту корабля капитан посылает торжественное приветствие человечеству как раз в тот момент, когда корабль пересекает горизонт событий. Его жест транслируется удаленным зрителям с помощью телевидения. Лента слева показывает, что происходит на корабле по его собственному времени, измеряемому часами на корабле, падающем в черную дыру. Приветствие космонавта разложено на отдельные кадры с промежутками между ними $0.2$ секунды собственного времени. Пересечение горизонта событий (у черных дыр нет твердой поверхности) не отмечено ничем примечательным. Пленка справа - то, что видят с помощью телевидения удаленные зрители. Она также разделена на отдельные кадры с интервалом $0.2$ секунды истинного времени. Вначале жест на экране лишь немного медленнее нестоящего, и кадры слева и справа практически идентичны. И только совсем рядом с горизонтом истинное время начинает стремительно замедляться; пленка справа изображает космонавта навечно застывшим в середине приветствия, бесконечно медленно приближающимся к последнему кадру, где он пересекает горизонт. Помимо этого, смещение частот в гравитационном поле (так называемый эффект Эйнштейна) приводит к тому, что картинка слабеет и скоро становится невидимой.
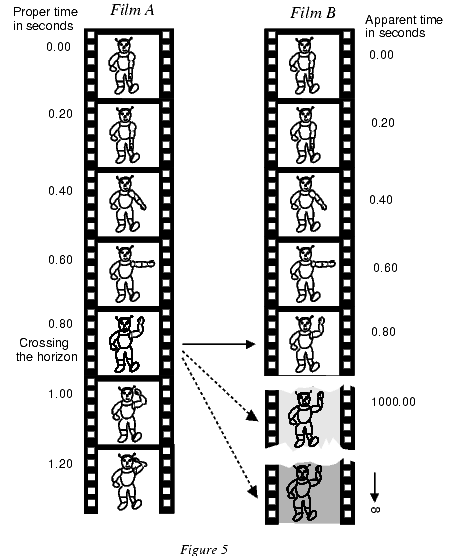
Рисунок 5. Приветствие космонавта.
Все эти эффекты достаточно очевидно следуют из уравнений. В общей теории относительности, пространство-время в пустоте вокруг сферически-симметричного тела описывается метрикой Шварцшильда (Schwarzschild)
$$ ds^2 = - \left(1- \frac{2M}{r}\right)dt^2 + \left(1-\frac{2M}{r}\right)^{-1}dr^2 + r^2 d\Omega^2, $$где $d\Omega^2 = d\theta^2 + sin^2\theta \;d\phi^2$ - метрика на единичной двумерной сфере, и мы положили постоянную тяготения $G$ и скорость света $c$ равными единице. Это решение описывает внешнее гравитационное поле вокруг произвольного сферически-симметричного не обязательно статического тела (теорема Биркгофа, Birkhoff's theorem, 1923; естественно, допустимые движения должны быть также сферически-симметричными, то есть чисто радиальными)
Когда радиус тела больше критического $2M$, существует внутреннее решение, зависящее от уравнения состояния вещества, которое не имеет сингулярности в центре и сшивается с внешним решением на поверхности. Однако, как только тело коллапсирует под сферу критического радиуса, метрика Шварцшильда становится единственным решением для гравитационного поля образовавшейся сферической черной дыры. Горизонт событий, сфера радиуса $r=2M$, является координатной сингулярностью, которой можно избежать надлежащим выбором системы координат. Истинная же сингулярность (в смысле расходимости инвариантов кривизны) находится в центре $(r=0)$ и не может быть устранена преобразованием координат. Однако сингулярность сама по себе не принадлежит пространственно-временному континууму.
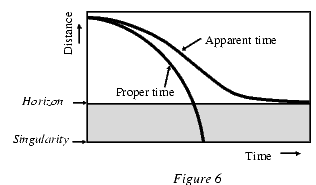
Рисунок 6. Два времени черной дыры.
Внутри горизонта событий радиальная координата $r$ становится времениподобной, и следовательно каждая частица, пересекшая горизонт, неизбежно захватывается центральной сингулярностью. Для радиального свободного падения вдоль траектории с $r \rightarrow 0 $, собственное время (измеряемое падающими часами) дается выражением
$$ \tau = \tau_0 - \frac{4M}{3}\left(\frac{r}{2M}\right)^{3/2} $$и не имеет особенностей на горизонте событий. Истинное время (измеряемое удаленным наблюдателем) имеет вид
$$ t = \tau - 4M\left(\frac{r}{2M}\right)^{1/2} + 2M \ln\frac{\sqrt{r/2M}+1}{\sqrt{r/2M}-1}, $$и расходится при $r \to 2M$, см. рисунок 6.
Координаты Шварцшильда, покрывающие только $2M \le r \lt \infty , - \infty \lt t \lt + \infty $, не вполне пригодны для анализа причинной структуры пространства-времени вблизи горизонта, так как световые цилиндры, описываемые как $dr = \pm (1-\frac{2M}{r})dt$, не определены на горизонте. Потому лучше использовать так называемые координаты Эддингтона-Финкельштейна (Eddington-Finkelstein coordinates) - открытые, однако, еще Леметром в 1933 году, но оставшиеся незамеченными. Вводя "падающую" координату
$$ v = t+r+2Mln(\frac{r}{2M}-1) $$преобразуем метрику Шварцшильда к виду
$$ ds^2 = - (1-\frac{2M}{r})dv^2 + 2 dvdr + r^2d\Omega^2. $$Теперь световые конусы определены везде. Направленные внутрь лучи света даются выражением
$$ dv = 0, $$а идущие наружу -
$$ dv = \frac{2dr}{1-\frac{2M}{r}}. $$Метрика может быть аналитически продолжена на все $r \gt 0$ и более не имеет сингулярности при $r=2M$. Действительно, на рисунке 4 эта координатная система была использована для всего пространства.
Несферический коллапс
Черные дыры могут также образовываться и при асимметричном гравитационном коллапсе. Однако деформации горизонта событий быстро диссипируют и уносятся излучением гравитационных волн; горизонт событий колеблется в соответствии с так называемыми "квазинормальными модами", и черная дыра эволюционирует к конечному осесимметричному равновесному состоянию.
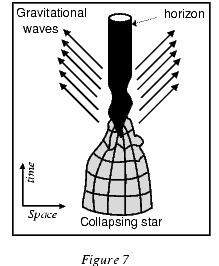
Рисунок 7. Гравитационный коллапс звезды.
Самым фундаментальным свойством черной дыры является то, что это асимптотическое равновесное решение зависит только от трех параметров - массы, электрического заряда и углового момента. Остальные особенности падающего вещества забываются. Доказательство следует из результатов пятнадцатилетней работы полудюжины ученых, но само это свойство изначально было высказано как предположение Джоном Уилером (John Wheeler), который использовал наглядную формулировку: "черные дыры не имеют волос".
Как следствие, есть только 4 точных решения уравнений Эйнштейна, описывающих черные дыры, имеющие или не имеющие заряд и угловой момент:
- Решение Шварцшильда (Schwarzschild, 1917) имеет только массу $M$ оно статично и сферически симметрично.
- Решение Рейсснера-Нордстрема (Reissner-Nordstr, 1918) статическое и сферически-симметричное, зависит от массы $M$ и электрического заряда $Q$.
- Решение Керра (Kerr, 1963), стационарное, осесимметричное, зависит от массы и углового момента.
- Решение Керра-Ньюмена (Kerr-Newman, 1965), стационарное и осесимметричное, зависит от всех трех параметров $M, J, Q$.
где $\Delta \equiv r^2 - 2 Mr + a^2 + Q^2$, $ \Sigma \equiv r^2 + a^2 cos^2\theta$, $a \equiv J/M$ - угловой момент на единицу массы. Горизонт событий находится на радиусе $r_+ = M + \sqrt{M^2 - Q^2 - a^2}$".
Из этой формулы видно, однако, что параметры черной дыры не могут быть произвольными. Электрический заряд и угловой момент не могут быть больше значений, соответствующих исчезновению горизонта событий. Должны выполняться следующие ограничения: $ a^2 + Q^2 \le M^2$.
Когда эти ограничения нарушаются, горизонт событий исчезает, и решение вместо черной дыры описывает "голую" сингулярность. Такие странные объекты не должны существовать в реальной вселенной, (это так называемый Принцип Космической Цензуры, строго до сих пор, к сожалению, не доказанный) К примеру, для незаряженной вращающейся черной дыры условие $J_{max} = M^2$ соответствует исчезновению тяготения на горизонте событий из-за приливных сил; соответствующая метрика называется предельным решением Керра. Аналогично, максимальный заряд равен $Q_{max} = M \approx 10^{40} e \, M/M_{\odot}$, где $e$ - заряд электрона; однако следует заметить, что в реалистичных ситуациях черные дыры не должны быть сколь либо значительно заряжены. Это является следствием предельной слабости гравитационного взаимодействия по сравнению с электромагнитным. Представьте черную дыру, образовавшуюся с положительным зарядом $Q$ порядка $M$. В реалистичной ситуации черная дыра не находится в пустоте, но окружена заряженными частицами межзвездной среды, протонами и электронами. Черная дыра будет преимущественно притягивать электроны и отталкивать протоны заряда $e$ своим электромагнитным полем, и преимущественно притягивать протоны массой $m_p$ гравитационным. Сила электромагнитного отталкивания для протона больше силы гравитационного притяжения в $eQ/m_pM \approx e/m_p \approx 10^{18}$. раз. Следовательно, черная дыра почти мгновенно теряет свой заряд, и решение Керра, получаемое при $Q=0$, может быть использовано для описания любой астрофизической черной дыры. Также оно является хорошим приближением для метрики обычной (несколлапсировавшей) звезды на больших расстояниях, хотя оно и не сшивается ни с одним известным решением для ее внутренних частей.
Метрика Керра в координатах Бойера-Линдквиста сингулярна на оси симметрии $\theta=0$ (это очевидная координатная сингулярность) и при $\Delta=0$. Можно записать $\Delta = (r-r_+)(r-r_-)$, где $r_+ = M +\sqrt{M^2 - a^2}$. На радиусе $r_+$ находится внешний горизонт событий (поверхность вращающейся черной дыры), а $r_-$ определяет внутренний горизонт. Как и в метрике Шварцшильда (где $r_+$ и $r_-$ сходятся к $2M$), сингулярности на $r=r_+$ и $r=r_-$ являются координатными, и их можно избежать надлежащим преобразованием системы координат по аналогии с координатами Эддингтона-Финкельштейна для метрики Шварцшильда. Строгое математическое исследование метрики Керра можно найти в работах Чандрасекара (Chandrasekhar, 1992) и О'Нейла (O'Neill, 1995)
Водоворот черной дыры
Можно заметить глубокое сходство вращающейся черной дыры и известного эффекта вихря - например, гигантского водоворота, порождения морских течений. Если мы посмотрим на срез светового конуса в фиксированный момент времени (горизонтальная плоскость на рисунке 8), полученное сечение будет "навигационным эллипсом", определяющим пределы возможных траекторий. Если световой конус значительно наклонится в гравитационном поле, точка излучения оказывается за пределами навигационного эллипса. Разрешенные траектории ограничены касательными к окружности, и возврат назад становится невозможен.
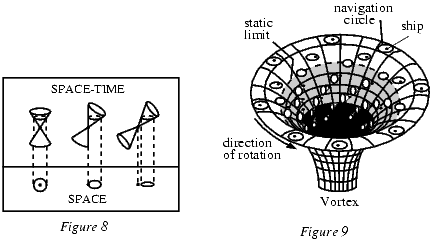
Рисунки 8 и 9. Навигационные окружности в водовороте черной дыры.
Этот метод проекций полезен для изображения причинной структуры пространства-времени вокруг вращающейся черной дыры (см. рисунок 9). Ее гравитационное поле напоминает космический водоворот. Пролетающий мимо космический корабль засасывается в центр как обычная лодка. Пока он находится вне так называемого предела статичности он еще может двигаться куда захочет. В области (показанной серым цветом) между пределом статичности и горизонтом событий он уже вынужден вращаться в том же направлении, что и черная дыра; его возможность свободного перемещения все более уменьшается при дальнейшем засасывании, но он еще может выбраться наружу, двигаясь по раскручивающейся спирали. Черным показана внутренность горизонта: оттуда уже нельзя спастись, даже двигаясь со скоростью света. Ситуацию прекрасно иллюстрирует повесть Эдгара По "Погружение в Мальстрем"(1840)
Предел статичности - это гиперповерхность вращения, определяемая уравнением $r = M + \sqrt{M^2 - a^2 cos^2\theta}$. Как видно из рисунка 10, она касается горизонта на полюсах $\theta = 0,\pi$ и лежит вне его для других значений $\theta$. Область между пределом статичности и горизонтом называют эргосферой. Любой находящийся там стационарный наблюдатель должен вращаться с положительной угловой скоростью. В эргосфере лежат траектории с отрицательной полной энергией. Это свойство породило идею извлечения энергии из вращающейся черной дыры. Роджер Пенроуз (Roger Penrose, 1969) предложил следующий механизм. Удаленный экспериментатор запускает снаряд в эргосферу по соответствующей траектории (рисунок 10). В эргосфере снаряд разделяется на две части, одна из которых падает в черную дыру, а вторая вылетает из эргосферы обратно к экспериментатору. Пенроуз показал, что можно выбрать такую траекторию для снаряда, что вернувшаяся половинка будет обладать большей энергией, чем исходный целый снаряд. Это возможно, если захваченная черной дырой половина снаряда падает по траектории с удельным моментом меньшим, чем у черной дыры, и, упав, уменьшает ее момент. В результате черная дыра теряет часть своей вращательной энергии, которая уносится второй половинкой снаряда.
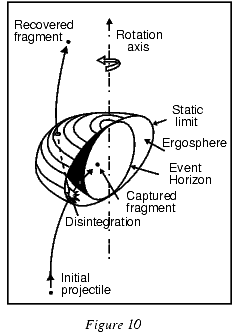
Рисунок 10. Сечение вращающейся черной дыры.
Количество энергии, которую можно извлечь из черной дыры, было посчитано Кристодулу и Руффини (Christodolou and Ruffini, 1971). Полная масса-энергия черной дыры есть
$$ M^2 = \frac{J^2}{4M_{ir}^2} + (\frac{Q^2}{4 M_{ir}} + M_{ir})^2 $$, где $M_{ir} \equiv \frac{1}{2}\sqrt{\left(M+\sqrt{M^2-Q^2-a^2}\right)^2+a^2}$. Первый член соответствует вращательной энергии, второй - кулоновской, а третий описывает "неприводимую" энергию черной дыры. Вращательная и кулоновская энергии могут быть извлечены, например, процессом Пенроуза, суперрадиацией (аналогом индуцированного излучения в атомной физике) или электродинамическими процессами, тогда как неприводимая часть не может быть уменьшена классическими (не квантовыми) процессами. Максимально извлекаемая энергия может достигать $29\%$ для вращательной и $50\%$ для кулоновской компонент. Это - гораздо большая эффективность, чем, скажем, для ядерного горения ($0.7\%$ для водорода).
Термодинамика черных дыр
Заметим, что неприводимая масса черной дыры связана с площадью горизонта черной дыры $A$ как $M_{ir} = \sqrt{A/16\pi}$. Соответственно, площадь горизонта событий не может уменьшаться со временем при любом классическом процессе. Это было впервые отмечено Стивеном Хокингом (Stephen Hawking), предложившим замечательную аналогию с обычной термодинамикой, в рамках которой энтропия системы никогда не уменьшается со временем. Это привело к тому, что в 70х годах прошлого века значительные теоретические усилия были направлены на изучение законов динамики черных дыр - например, законов, описывающих изменения массы, площади поверхности и других характеристик при взаимодействии черной дыры с остальной вселенной - а также развитие и углубление аналогий с классической термодинамикой. Эволюция черных дыр управляется четырьмя законами, соответствующими четырем началам классической термодинамики:- Нулевое начало.
В механике черных дыр: все участки горизонта событий равновесной черной дыры имеют одинаковую поверхностную гравитацию $g$. Поверхностная гравитация определяется формулой Смарра (Smarr) $M = gA/4\pi + 2 \Omega_HJ + \Phi_H Q$, где $\Omega_H$ - угловая скорость на горизонте и $\Phi_H$ - электрический потенциал в синхронно с горизонтом вращающейся системе отсчета. Это достаточно интересное свойство по сравнению с обычными небесными телами, для которых поверхностная гравитация зависит от широты. Но, так как черная дыра немного сплющивается под действием центробежных сил, для нее эта величина постоянна во всех точках поверхности.
- Первое начало.
В динамике черных дыр: бесконечно малая вариация массы $M$, заряда $Q$ и углового момента $J$ при возмущении стационарной черной дыры связаны как $dM = \frac{g}{8\pi}dA + \Omega_H dJ +\Phi_H dQ$.
- Второе начало.
В динамике черных дыр, площадь поверхности черной дыры не может уменьшаться: $dA \ge 0$.
Это начало говорит, например, что площадь поверхности черной дыры, получающейся при слиянии двух меньших, больше суммы их площадей (см; рисунок 11). Отсюда также следует, что черная дыра не может фрагментировать, то есть ее нельзя разделить на 2 части.
- Третье начало.
В механике черных дыр, невозможно снизить поверхностную гравитацию до нуля конечным числом операций. Для керровских черных дыр мы видели, равенство нулю поверхностной гравитации соотсвтствует "предельному" решению $J=M^2$.
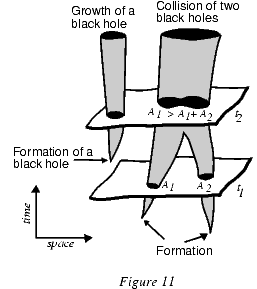
Рисунок 11. Необратимый рост черных дыр.
Видно, что площадь поверхности черной дыры играет формально роль энтропии, в то время как поверхностная гравитация - роль температуры. Однако, как впервые заметил Бекенштейн (Bekenstein), если бы у черной дыры была температура, как у обычной термодинамической системы, она должна была бы терять энергию на излучение, в противоречии со сформулированными выше основными свойствами. Эта загадка была решена Стивеном Хокингом, когда он открыл испарение черных дыр в результате квантовых процессов.
Квантовая черная дыра
Попробуем на пальцах разобраться, что такое хокинговское излучение (см. рисунок 12). Пусть гравитация черной дыры описывается (классической) общей теорией относительности, тогда как окружающий вакуум - квантовой теорией поля. Квантовое испарение аналогично процессу рождения пар в сильном магнитном поле за счет поляризации вакуума. В море Ферми пар частиц-античастиц, постоянно рождающихся и аннигилирующих, возможны четыре процесса, схематически изображенных на рисунке 12.
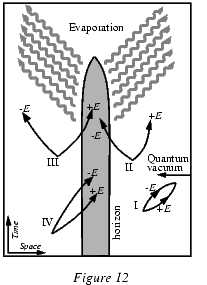
Рисунок 12. Квантовое испарение черной дыры за счет поляризации вакуума.
Некоторые пары частиц, родившись из квантовых флюктуаций, просто аннигилируют вне горизонта (процесс I). Другие, возникшие слишком близко к нему, безвозвратно исчезают в черной дыре (процесс IV). Другие же разделяются - одна из частиц захватывается черной дырой, в то время как другая улетает прочь (процессы II и III). Расчеты показывают, что преимущественно реализуется процесс II, так как (классический) гравитационный потенциал поляризует квантовый вакуум. Как следствие, черная дыра излучает частицы с тепловым спектром, причем характеристическая температура точно описывается формулой, следующей из термодинамической аналогии:
$$ T = \hbar \,\frac{g}{2\pi} = 10^{-7} \frac{M_{\odot}}{M} \textrm{K}, $$где $\hbar$ - постоянная Планка. Легко видеть, что температура пренебрежимо мала для любой астрофизической черной дыры с массой порядка солнечной. Однако для "миниатюрных" черных дыр с массами $10^{15}$ грамм (типичная величина для астероида) хокинговская температура становится порядка $10^{12} K$. Время "испарения" черной дыры за счет излучения примерно определяется выражением
$$ t_E \approx 10^{10} years \, \left(\frac{M}{10^{15} grams}\right)^3 $$Соответственно, черные дыры с массой, меньшей типичной массы астероида (и размером меньше $10^{-13}$ см) испаряются на временах, меньших время жизни вселенной. Некоторые из них должны испаряться прямо сейчас, давая огромные всплески жесткого излучения. Но ничего подобного до сих пор не наблюдалось (гамма-всплески объясняются совершенно по-другому). Такое наблюдательное ограничение дает верхний предел на плотность мини-черных дыр $100 /(\textrm{св. год})^3$.
Энтропия черной дыры определяется как
$$ S = \frac{k_B}{\hbar} \frac{A}{4} $$(где $k_B$ - постоянная Больцмана), что в числах дает $S \approx 10^{77} k_B(\frac{M}{M_{\odot}})^2$ для шварцшильдовской черной дыры. Так как энтропия несколлапсировавшей звезды типа Солнца по порядку величины равна $10^{58} k_B$, можно отметить глубокий смысл "теоремы об отсутствии волос" у черной дыры - черная дыра является огромным резервуаром энтропии. Из-за хокинговского излучения уменьшается неприводимая масса, или, что то же самое, площадь горизонта черной дыры, что нарушает Второе Начало термодинамики черных дыр. Оно должно быть обобщено - в него надо добавить учет энтропии во внешнем пространстве-времени. Тогда полной энтропией излучающей черной дыры будет $S = S_{BH} + S_{ext}$, где, так как хокинговское излучение является тепловым, $S_{ext}$ растет, и в конечном счете $S$ всегда будет неубывающей функцией.
В заключение вопроса отметим, что даже если мини-черные дыры очень редки, или даже совсем отсутствуют во вселенной (например, если Большой Взрыв не дал подобных флюктуаций пространства-времени) - они все равно являются огромным шагом вперед в нашем понимании связи гравитации и квантовой теории.
Отображения пространства-времени
Различные математические методики позволяют геометру надлежащим образом изобразить сложную структуру пространства-времени, образуемую черными дырами.
Диаграмма погружения -- Пространство-время, индуцируемое сферической массой $M$, описывается метрикой Шварцшильда:
$$ ds^2 = - \left(1- \frac{2M(r)}{r}\right)dt^2 + \left(1-\frac{2M(r)}{r}\right)^{-1}dr^2 + r^2 d\Omega^2 $$где $M(r)$ - масса, заключенная внутри радиуса $r$. Так как геометрия статична и сферически-симметрична, мы не потеряем существенной информации, если будем рассматривать только экваториальный срез $\theta = \pi/2$ в фиксированный момент времени $t=constant$. Мы тогда получаем искривленную 2--геометрию с метрикой $(1-\frac{2M(r)}{r})^{-1}dr^2 + r^2 d\phi^2$. Эта поверхность может быть наглядно представлена погружением ее в евклидово 3--пространство $ds^{2} = dz^{2} + dr^{2} + d\phi^{2}$. Для несколлапсировавшей звезды радиуса $R$ внешнее решение $z(r) = \sqrt{8M(r-2M)}$ при $r\geq R \ge 2M$ является асимптотически плоским и сшивается с несингулярным внутренним решением $z(r) = \sqrt{8M(r)(r-2M(r))}$ при $0 \le r\le R$ (рисунок 13). Для черной дыры такое погружение определено только для $r \geq 2M$. Соответствующая поверхность - параболоид Фламма (Flamm) $z(r) = \sqrt{8M(r-2M)}$. Такая асимптотически плоская поверхность состоит из двух параллельных плоскостей, соединенных "горловиной Шварцшильда" радиуса $2M$. Две плоскости можно рассматривать или как две различных асимптотически плоских "параллельных" вселенных (какой бы физический смысл за этим ни стоял), в которых черная дыра верхней соединена с обращенной во времени "белой дырой" нижней вселенной (рисунок 14), или как одно асимптотически плоское пространство-время, содержащее пару черной и белой дыр, соединенных так называемой "червячной норой" (рисунок 15). Такая свобода интерпретации следует из топологической неопределенности общей теории относительности, которая позволяет нам отождествить между собой некоторые удаленные точки пространства-времени, не меняя локальной метрики.
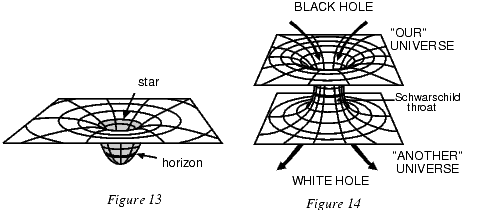
Рисунки 13 и 14. Погружение несколлапсировавшей сферической звезды (13) и метрики Шварцшильда.
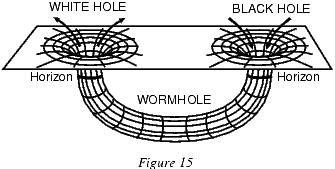
Рисунок 15. Кротовая нора в пространстве-времени.
Однако, методика погружения не дает возможности исследовать области пространства-времени внутри горизонта событий.
Диаграмма Крускала (Kruskal) -- Используем для анализа внутренней структуры пространства-времени максимальное аналитическое продолжение метрики Шварцшильда. Это достигается преобразованием координат, открытым Крускалом:
$$ u^{2} - v^{2} = (\frac{r}{2M}-1)e^{r/2M} $$ \begin{eqnarray} \frac{v}{u} = \left\{\begin{array}{c}\coth {t\over4M}\\1\\\tanh {t\over4M}\end{array}\right\} \quad\textrm{for}\quad r\left\{\begin{array}{c} < 2M\\=2M\\>2M\end{array}\right\}\nonumber. \end{eqnarray}Метрика тогда переходит в
$$ ds^{2} = \frac{32M^3}{r} e^{-r/2M}(-dv^{2} + du^{2})+ r^{2}d\Omega^{2} $$В плоскости $(v,u)$ пространство-время Крускала разделяется на две внешних асимптотически плоских области и два региона внутри горизонта событий, ограниченных сингулярностями прошлого и будущего. Только незакрашенная область покрывается координатами Шварцшильда. Черная область лежит вне пространства-времени. На диаграмме Крускала (рисунок 16) свет всегда движется под углом $45^{\circ}$, линии постоянного радиуса - гиперболы, линии постоянного времени походят через начало координат. Внутри горизонта событий будущего лежит черная дыра, горизонта событий прошлого - белая. Однако ясно, что через кротовую нору нельзя пройти по времениподобной траектории: ни одна траектория не может вести из одной вселенной в другую, не проходя через сингулярность при $r=0$.
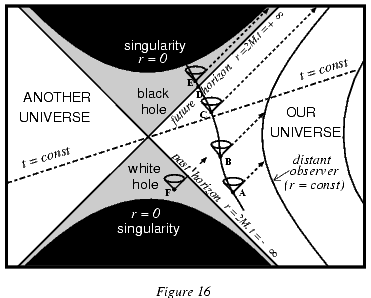
Рисунок 16. Изучение сферической черной дыры с помощью диаграммы Крускала.
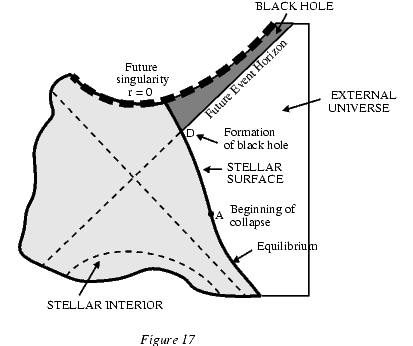
Рисунок 17. Урезанная диаграмма Крускала, описывающая коллапс звезды в черную дыру.
Более того, продолжение Крускала - не более чем математическая идеализация черной дыры по той причине, что она неявно предполагает то, что черная дыра существует вечно. Однако для реальной вселенной черная дыра не прописана жестко в начальных условиях, она может образоваться только в результате гравитационного коллапса. В этом случае мы имеем "урезанную" диаграмму Крускала( рисунок 17), содержащую только горизонт событий и сингулярность будущего, находящиеся в асимптотически плоском пространстве-времени. А это не дает ни единого шанса для путешествий в пространстве-времени...
Диаграммы Пенроуза-Картера (Penrose, Carter) -- Диаграммы Пенроуза-Картера используют конформное преобразование координат $g_{\alpha \beta} \to \Omega^{2}g_{\alpha \beta}$, отображающее пространственно- и времениподобные бесконечности на конечные расстояния, что дает возможность отобразить пространство-время внутри квадрата. Диаграмма Пенроуза-Картера для шварцшильдовской черной дыры не дает новой информации по сравнению с крускаловской, но, наверно, является лучшим инструментом для изучения сложной пространственно-временной структуры вращающейся черной дыры. Рисунок 18 изображает многослойную структуру решения Керра; он показывает, что некоторые времениподобные траектории ($B,C$) могут пересекать внешний $EH$ и внутренний $IH$ горизонты событий и переходить из одной асимптотически плоской внешней вселенной в другую, не проходя при этом сквозь сингулярности. Это является следствием того, что сингулярность $S$ времени-, а не пространственноподобна. Кроме того, по форме сингулярность представляет собой кольцо в экваториальной плоскости, так что некоторые траектории ($A$) могут проходить через это кольцо и попадать в асимптотически плоское пространство-время внутри черной дыры, где гравитация является силой отталкивания. Однако, анализ возмущений такой идеализированной Керровской дыры показывает, что она неустойчива, и потому не физически маловероятна.
То, что общая теория относительности предсказывает существование черных дыр и в то же время является заслуживающей доверия теорией гравитации, еще само по себе не доказывает существования черных дыр во вселенной, так как эта теория не описывает астрофизические процессы, в которых черные дыры образуются.
Таким образом, астрофизическая состоятельность идеи черных дыр существенно зависит от хорошего понимания гравитационного коллапса звезд и их скоплений.
В этом разделе мы сначала кратко обсудим астрофизические условия для формирования черных дыр, а затем расскажем, в каких астрономических ситуациях следует ожидать их наличия.
Образование черных дыр звездных масс
Основной процесс звездной эволюции - это гравитационное сжатие с темпом, определяемым светимостью. Ключевой параметр - начальная масса. В зависимости от ее величины звезда эволюционирует через различные стадии ядерного горения и оканчивает свои дни как белый карлик, нейтронная звезда или черная дыра. Любой звездный остаток (холодная равновесная конфигурация) с массой, большей примерно $3 M_{\odot}$, не может поддерживаться давлением вырожденного газа и обречен сколлапсировать в черную дыру.
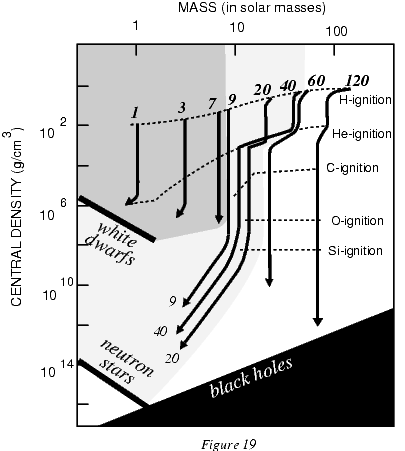
Рисунок 19. Диаграмма "плотность-масса" для астрономических объектов.
На рисунке 19 показаны траектории звезд на диаграмме "масса -- средняя плотность" в соответствии с последними наблюдательными и теоретическими данными. Звезды с массой меньше $8 M_{\odot}$ оканчивают жизнь как белые карлики, между $8$ и $45 M_{\odot}$ - как нейтронные звезды; черные дыры образуются только из звезд массивнее $45 M_{\odot}$ (для звезд с массами между $20$ и $40 M_{\odot}$ существенна потеря массы на стадии горения гелия). Принимая во внимание начальное распределение звезд по массам, мы получаем примерно 1 черную дыру на 100 взрывов сверхновых. Другим вариантом образования черной дыры звездной массы является аккреция газа на нейтронную звезду в двойной системе до тех пор, пока масса последней не превзойдет предела Оппенгеймера-Волкова - максимально возможной массы нейтронной звезды; тогда она коллапсирует в маломассивную черную дыру.
Учитывая все эти процессы, мы получаем, что в типичной галактике типа нашей должно быть порядка $10^7 - 10^8$ черных дыр звездных масс.
Образование сверхмассивных черных дыр
Массивные черные дыры могут возникать в результате постепенного роста "затравочной" дыры звездной массы, гравитационного коллапса большого звездного скопления или коллапса больших флюктуаций плотность в ранней вселенной (см. следующий раздел). Маленькая черная дыра при соответствующей "подкормке" может дорасти до сверхмассивной за время меньше хаббловского. Это требует большого количества вещества в ее окрестности, что может иметь место в некоторых галактических ядрах.
Эволюция компактного скопления обычных звезд с дисперсией скоростей $v_c \leq v_*$, где $v_* \approx 600$ км/с - типичная скорость убегания для звезды главной последовательности, вначале проходит стадию ядерного горения отдельных звезд; во взрывах сверхновых образуются звездные остатки - нейтронные звезды и маломассивные черные дыры. Скопление компактных звезд, как было показано Зельдовичем и Подурецом, подвержено релятивистской неустойчивости при достаточно больших центральных красных смещениях $1+z_c = (1-2M)^{-1/2} \geq 1.5$ (Zeldovich, Podurets, 1965). Численное моделирование (см. работы Shapiro и Teukolsky, 1987, Bisnovatyi-Kogan, 1988) подтверждают такое развитие событий. Начиная с $\approx 10^7 - 2.10^8$ компактных звезд с массами $1-10 M_{\odot}$ в скоплении с радиусом $r \leq 0.01 - 0.1 \,$ парсек и дисперсией скоростей $800-2000 \, $км/с, эволюция проходит через три стадии:
- постепенный коллапс ядра из-за гравитепловой катастрофы (большие времена)
- короткая эпоха доминирования столкновений и слияний компактных объектов, в результате которой формируются черные дыры массы $M \approx 90 M_{\odot}$
- развитие релятивистской неустойчивости, приводящее к формированию массивной черной дыры, окруженной гало из звезд.
Формирование миниатюрных черных дыр
Зельдович в 1967 и Хокинг в 1971 годах показали, что в принципе возможно создание черной дыры малой массы (меньше предела Чандрасекара) при приложении достаточно сильного внешнего давления. Нужные для этого условия могли иметь место, однако, только в очень ранней вселенной. Силы притяжения могут локально остановить расширение части вещества и обратить его в коллапс, если самогравитация вещества превышает его внутреннюю энергию:
$$ \frac{GM^2}{R} \approx G\rho ^2 R^5 \geq pR^3 $$В эру доминирования излучения $p \approx \rho c^2$, потому вышеприведенное условие равносильно $GM/c^2 \geq R$, где $R$ - размер неоднородности. Тогда формируется первичная черная дыра массы $M$. Из-за зависимости плотности от времени в модели ранней вселенной Эйнштейна-де Ситтера как $G\rho \approx t^{-2}$ максимальный размер коллапсирующей неоднородности связан с возрастом вселенной как $M(\textrm{грамм}) \approx 10^{38} t$, где время выражено в секундах. Потому на возрасте порядка планковского времени $t \approx 10^{-43}$с. могли сформироваться только черные дыры планковской массы $\approx 10^{-5}$ г, на времени $t \approx 10^{-4}$с. массы черных дыр могут достигать $\approx 1 M_{\odot}$, а в эпоху нуклеосинтеза $t \approx 100 \,$ могли сформироваться сверхмассивные черные дыры с $10^7 M_{\odot}$. Наблюдательный статус первичных черных дыр неясен. С одной стороны, миниатюрные черные дыры с массой $\leq 10^{15}$ грамм могли бы быть зафиксированы по вспышкам гамма-излучения на последних стадиях квантового испарения. Ничего подобного до сих пор не наблюдалось, что позволяет получить некоторые верхние пределы на их среднюю плотность во вселенной. С другой стороны, тот факт, что в большинстве галактических ядер, похоже, находятся массивные черные дыры (см. ниже) и что сверхмассивные черные дыры, как полагают, обеспечивают энергетику квазаров на больших красных смещениях, говорит в пользу гипотезы о быстром образовании первичных черных дыр в ранней вселенной.
Кандидаты в черные дыры в рентгеновских двойных системах
Даже свет не может покинуть (классические) черные дыры, но можно надеяться обнаружить их косвенно, по излучению, выделяющемуся в процессе аккреции на них.
Аккреция газа на компактную звезду генерирует излучение в рентгеновском диапазоне, потому поиск черных дыр звездных масс состоит в отборе быстропеременных рентгеновских источников, которые не являлись бы ни периодическими (соответствующие рентгеновские пульсары интерпретируются как вращающиеся нейтронные звезды), ни вспыхивающими время от времени (соответствующие рентгеновские барстеры интерпретируются как термоядерные взрывы на твердой поверхности нейтронной звезды). В спектральных двойных кривая лучевых скоростей главной (видимой) компоненты определяет орбитальный период $P$ двойной системы и амплитуду лучевой скорости главной компоненты Кеплера, можно построить функцию масс, связывающую наблюдательные величины с неизвестными массами:
$$ \frac{Pv_{*}^3}{2 \pi G} = \frac{(M_{c}\sin i)^{3}}{(M_{*}+M_{c})^{2}} $$где $M_{c}$ и $M_{*}$ - массы компактного объекта и оптической звезды, $i$- угол наклона плоскости орбиты. Замечательно то, что $M_{c}$ не может быть меньше значения этой функции масс (и равна ему в пределе нормальной компоненты нулевой массы на максимально возможном угле наклона орбиты). Поэтому наилучшими кандидатами в черные дыры будут те, для которых функция масс превосходит $3M_{\odot}$ -- так как, согласно современным теоретическим представлениям масса нейтронной звезды не может превышать этот предел. Иначе для оценки $M_{c}$ требуется дополнительная информация: спектральный тип оптической звезды дает ее примерную массу, наличие или отсутствие рентгеновских затмений позволяет оценить $\sin i$. Таким образом получаются некоторые ограничения на $M_{c}$. Объект считается кандидатом в черные дыры, только если ограничение снизу превышает $3 M_{\odot}$. На сегодняшний день известно около десятка хороших кандидатов в рентгеновских двойных системах. Их можно разделить на две группы: массивные рентгеновские двойные (high--mass X--ray binaries, HMXB) с массивной оптической компонентой и маломассивные двойные (low--mass X--ray binaries, LMXB), для которых типичная масса оптического компонента меньше солнечной. Маломассивные рентгеновские двойные называют также рентгеновскими транзиентами (X-ray transients), так как они изредка вспыхивают до очень больших светимостей. Их параметры суммированы в таблице 1.
| функция масс | $M_{c}/M_{\odot}$ | $M_{*}/M_{\odot}$ | |
|---|---|---|---|
| массивные рентгеновские двойные | |||
| Cygnus X-1 | 0.25 | 11-21 | 24-42 |
| LMC X-3 | 2.3 | 5.6 -7.8 | 20 |
| LMC X-1 | 0.14 | $\geq$ 4 | 4-8 |
| маломассивные рентгеновские двойные (рентгеновские транзиенты) | |||
| V 404 Cyg | 6.07 | 10--15 | $\approx$ 0.6 |
| A 0620-00 | 2.91 | 5--17 | 0.2--0.7 |
| GS 1124-68 (Nova Musc) | 3.01 | 4.2--6.5 | 0.5--0.8 |
| GS 2000+25 (Nova Vul 88) | 5.01 | 6-14 | $\approx$ 0.7 |
| H 1705-25 (Nova Oph 77) | 4.65 | 5--9 | $\approx$ 0.4 |
| GRO J 1655-40 | 3.24 | 4.5 -- 6.5 | $\approx$ 1.2 |
| J 04224+32 | 1.21 | 6--14 | $\approx$ 0.3 -- 0.6 |
Другие рентгеновские источники в нашей галактике считаются черными дырами на основании иных - например, спектроскопических - аргументов. К примеру, полагают, что гамма-излучение (с энергиями более $100$ кэВ) внутренних частей аккреционного диска могло бы свидетельствовать о наличии черной дыры, а не нейтронной звезды, так как жесткое излучение отражалось бы поверхностью нейтронной звезды и охлаждало диск. Если это действительно так, то многие "гамма - новые", в которых измерение массы невозможно (из-за отсутствия оптической компоненты или иных сложностей), могут быть также хорошими кандидатами в черные дыры. Особенно это относится к Новой Орла 1992 года (Nova Aquila 1992) и источнику 1 E 17407-2942, у которых наблюдаются также радиовыбросы - "джеты". Эти "микроквазары", в которых идет как аккреция, так и выброс вещества, демонстрируют интересную связь высокоэнергичных явлений на масштабах звезд и галактик.
Свидетельства существования сверхмассивных черных дыр в ядрах галактик
После оригинальных рассуждений Митчелла и Лапласа идея гигантских черных дыр была вновь привлечена в 60-е годы прошлого века для объяснения огромного энерговыделения активных галактических ядер (active galactic nuclei, AGNs). Это - общее название для огромного семейства галактик, включающего в себя квазары, радиогалактики, сейфертовские галактики, блазары и так далее. Основным процессом в них является аккреция газа на массивную черную дыру. Предельная светимость для источника массой $M$, называемая эддингтоновской светимостью, определяется из равенства сил гравитационного притяжения и давления излучения на элемент газа и равна
$$ L \approx 10^{39} \, \frac{M}{10^{8}M_{\odot}} \textrm{Ватт} $$Наблюдаемые светимости активных галактических ядер варьируются от $10^{37}$ до $10^{41}$ Ватт, где последняя величина соответствует наиболее мощным квазарам. Соответствующие значения масс лежат в пределах $10^{6} - 10^{10} M_{\odot}$.
Благодаря постоянному улучшению наблюдательных данных, в 90-х годах стало ясно, что в большинстве галактических ядер (как активных, так и нет) сконцентрированы большие массы вещества. Сегодня обнаружение этих масс - одна из главных задач внегалактической астрономии. Наиболее успешным методом является анализ динамики окружающего ядро вещества: газ или звезды вблизи невидимой центральной массы имеют большую дисперсию скоростей, что может быть измерено спектроскопически. Похоже, что массивные черные дыры сидят в центрах почти всех галактик, а энергетика их определяется имеющимся объемом газа. Наилучшие кандидаты суммированы в таблице 2.
К примеру, центр нашей галактики наблюдается в радио. инфракрасном и рентгеновском диапазонах (на других длинах волн слишком велико поглощение пылевыми облаками в галактическом диске). Необычный радиоисточник был обнаружен в динамическом центре, что можно интерпретировать как среднемассивную черную дыру с малым темпом аккреции. Однако однозначного доказательства этому пока нет, так как наблюдаемые движения газа трудно интерпретировать. Недавно Экартом и Гензелом (Eckart, Genzel, 1996) было получено полное трехмерное распределение звездных скоростей в центральных 0.1 пк нашей галактики. Значения и распределение их хорошо согласуются с гипотезой наличия там черной дыры с массой $2.5 \times 10^{6} M_{\odot}$.
Ядро гигантской эллиптической галактики $M87$ в скоплении Девы также давно привлекает внимание как кандидат в сверхмассивные черные дыры. Независимые наблюдения согласуются с моделью черной дыры с массой $1-3 \, 10^{9} M_{\odot}$, аккрецирующей в медленном неэффективном режиме. Газовый диск вращается в плоскости, перпендикулярной наблюдаемому выбросу; недавние наблюдения на космическом телескопе имени Хаббла показывают компоненты диска с красным и синим смещением, что можно интерпретировать как эффект Доплера при приближении и удалении от нас частей диска.
Ядро спиральной галактики NGC 4258 (M 106) является, пожалуй, самым надежным кандидатом в массивные черные дыры. Движения газа там промерены с большой точностью по мазерной линии излучения $1.3$ см $H_{2}O$. Скорости известны с точностью до $1$ км/с. По их пространственному распределению виден диск с кеплеровским вращением вокруг массивного компактного объекта, причем радиус внутреннего края диска, где орбитальная скорость газа составляет $1080$ км/с, слишком мал, чтобы внутри него могло находиться устойчивое скопление звезд массой $3.6 \times 10^{7}M_{\odot}$.
| динамика | галактика | тип галактики | $M_{h}/M_{\odot}$ |
|---|---|---|---|
| мазер | M 106 | с баром | $ 4 \times 10^{7}$ |
| газ | M 87 | эллиптическая | $ 3 \times 10^{9}$ |
| газ | M 84 | эллиптическая | $ 3 \times 10^{8}$ |
| газ | NGC 4261 | эллиптическая | $ 5 \times 10^{8}$ |
| звезды | M 31 | спиральная | $3-10 \times10^{7}$ |
| звезды | M 32 | эллиптическая | $ 3 \times 10^{6}$ |
| звезды | M 104 | спиральная (с баром?) | $ 5-10 \times 10^{8}$ |
| звезды | NGC 3115 | линзовидная | $ 7-20 \times 10^{8}$ |
| звезды | NGC 3377 | эллиптическая | $ 8 \times 10^{7}$ |
| звезды | NGC 3379 | эллиптическая | $ 5 \times 10^{7}$ |
| звезды | NGC 4486B | эллиптическая | $ 5 \times 10^{8}$ |
| звезды | Milky Way | спиральная | $ 2.5 \times 10^{6}$ |
Массивные черные дыры в нашей и соседних галактиках должны быть уменьшенными версиями тех сильно нестационарных явлений, что наблюдаются в активных галактических ядрах. Но последние слишком далеки, чтобы можно было проводить спектроскопическое исследование их динамики. Однако, оценки их светимости и теоретические ограничения на эффективность энерговыделения в сильных гравитационных полях показывают, что центральные темные массы там заключены в пределах $10^{7} - 10^{9} \, M_{\odot}$. Переменность излучения на малых временах также свидетельствует о малых размах излучающих областей; многие активные ядра сильнопеременны на временных шкалах порядка часа, что ограничивает область излучения масштабом светового часа. А такие большие массы в таких малых объемах не могут быть скоплениями звезд, потому аккрецирующие массивные черные дыры остаются единственным приемлемым объяснением.
Разрушение звезд
Светимость при аккреции газа с темпом $dM/dt$ и типичной эффективностью $\epsilon \approx 0.1$ есть
$$ L \approx 10^{39} (\frac{\epsilon}{0.1}) \, \frac{dM/dt}{1 M_{\odot}/\textrm{год}}\textrm{Ватт} $$Сравнивая светимость этой модели аккреции с наблюдаемыми для активных галактических ядер, мы получаем пределы на темп аккреции $10^{-2}- 10^{2} \, M_{\odot}/\textrm{год}$. Дальше встает вопрос, какой именно механизм способен его обеспечить для гигантской черной дыры. Достаточно эффективна, например, потеря массы пролетающими рядом звездами. Современные модели галактических ядер предполагают массивную черную дыру, окруженную плотным звездным облаком. Из-за диффузии орбит некоторые звезды залетают достаточно глубоко в гравитационных потенциал черной дыры по сильно вытянутым орбитам. Звезды могут разрушаться либо под действием приливных сил, либо за счет столкновений с другими звездами (см. рисунок 20). Радиус столкновений $R_{coll} \approx 7 \times 10^{18} \, \frac{M}{10^8 M_{\odot}}$ см для солнцеподобных звезд определяется как расстояние, на котором скорость свободного падения сравнивается со скоростью убегания на поверхности звезды $v_{*}$ (порядка $500$ км/с для нормальных звезд); при столкновении двух звезд внутри $R_{coll}$ они частично или полностью разрушаются.
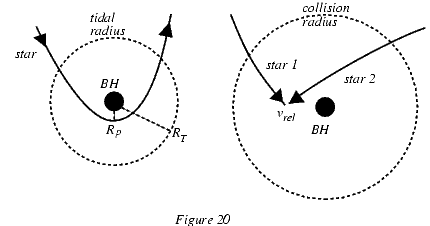
Рисунок 20. Приливной радиус и радиус столкновений.
Кроме того, звезды, попавшие внутрь критического приливного радиуса $R_{T} \approx 6\times 10^{13} \, ( \frac{M}{10^{8}M_{\odot}} )^{1/3}$ см. для солнцеподобных звезд, будут неизбежно разрушены приливными силами, примем порядка $50\%$ их газа будет захвачено черной дырой. В некотором смысле такое разрушение можно рассматривать как столкновение звезды с самой собой...
В случае столкновения величина $\beta = v_{rel}/v_{*}$ играет ту же роль, что и фактор $\beta = R_{T}/R_{p}$ в случае разрушения приливными силами (где $R_{p}$ - высота периастра). Как только выполняется условие $\beta \geq 1$, звезда разрушается, а когда $\beta \geq 5$, звезды сильно деформируются при столкновении, то есть в обоих случаях $\beta$ является фактором разрушения, величина которого определяет судьбу звезды.
Впервые приливное разрушение звезды массивной черной дырой было промоделировано в 80-х годах мной с сотрудниками (см. работу Luminet и Carter, 1986, и ссылки в ней). Мы установили, что звезда, попавшая внутрь сферы приливного радиуса, сдавливается приливными силами в короткоживущий очень горячую блиноподобную конфигурацию. Рисунок 21 показывает процесс деформации звезды (размер ее значительно увеличен для выразительности). Слева показана деформация звезды в плоскости ее орбиты, а справа - в перпендикулярном направлении. От $a$ до $d$ приливные силы слабы, и звезда остается почти сферической. В точке $e$ звезда проходит приливной радиус и становится сигарообразной. От $e$ до $g$ становится все более важным "эффект катка", и звезда уплощается в орбитальной плоскости до формы изогнутого "блина". Когда звезда покидает сферу приливного радиуса, пролетев вблизи черной дыры, она вновь расширяется, вновь становится сигарообразной. Чуть позже звезда наконец разваливается на куски.
Если же звезда пролетает достаточно близко от черной дыры (скажем, на $\beta \geq 10$), ее центральная температура за долю секунды возрастает до миллиарда градусов, сильно увеличивается скорость термоядерных реакций, такие элементы, как гелий, азот и кислород мгновенно переходят в более тяжелые за счет захвата протонов или альфа-частиц. В "звездном блине" происходит термоядерный взрыв, давая в результате "случайную сверхновую". Этот взрыв имеет далеко идущие последствия: порядка $50\%$ звездных "обломков" выбрасываются (за счет энергии взрыва) с огромной скоростью прочь от черной дыры горячим газовым облаком, остальное вещество падает на черную дыру, вызывая вспышку излучения. Как и сверхновые, "звездные блины" являются теми тиглями, в которых рождаются тяжелые элементы, потом рассеиваемые по всей галактике. Таким образом, наблюдения высокоскоростных облаком и необычно высокого обилия редких изотопов в окрестностях галактических ядер могло бы послужить аргументом в пользу наличия там черных дыр.
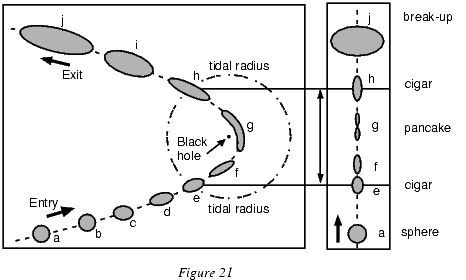
Рисунок 21. Разрушение звезды приливными силами вблизи черной дыры.
Сопровождаемое взрывом или нет, приливное разрушение звезды должно вызывать вспышку излучения на шкале нескольких месяцев (столько требуется веществу звезды, чтобы полностью исчезнуть в черной дыре). Для описания эволюции звезды нами была разработана приближенная "аффинная модель", предполагающая эллипсоидальность слоев постоянной плотности. Многие астрофизики сомневались в предсказаниях такой модели до тех пор, пока по всему миру не были проведены детальные трехмерные расчеты, подтвердившие ее основные свойства и предсказания (хотя формирование ударных волн и может немного понизить центральную плотность "блина").
В промежутке между 1991 и 1993 годами ультрафиолетовая светимость ядра эллиптической галактики NGC 4552 возросла до $10^{6} L_{\odot}$ на шкале времени, согласующейся с предсказаниями теории приливного разрушения звезды, хотя светимость и оказалась примерно на 4 порядка ниже, чем ожидалось, что может свидетельствовать о неполном разрушении звезды.
Путешествие в черную дыру
Представьте черную дыру, окруженную ярко светящимся диском (рисунок 22). Система рассматривается с большого расстояния под углом $10^{\circ}$ к плоскости диска. Свет принимается фотопластинкой (или даже болометром, для учета излучения всех диапазонов длин волн). Из-за кривизны пространства-времени в окрестности черной дыры изображение системы существенно отличается от эллипсов, которые мы бы видели, если б заменили черную дыру обычным маломассивным небесным телом. Излучение верхней стороны диска образует прямое изображение, причем из-за сильной дисторсии мы видим весь диск (черная дыра не закрывает от нас находящиеся за ней части диска). Нижняя часть диска также видима из-за существенного искривления световых лучей.
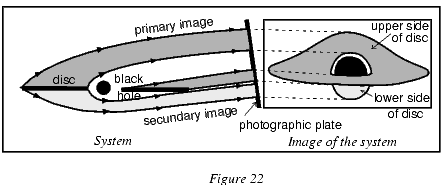
Рисунок 22. Оптические искажения вблизи черной дыры.

Рисунок 23. Так издали выглядит черная дыра, окруженная аккреционным диском.
Первые компьютерные картинки черной дыры, окруженной аккреционным диском, были получены мной (Luminet, 1978). Более тонкие расчеты проведены Марком (Marck, 1993) как для метрики Шварцшильда, так и для случая вращающейся черной дыры. Правдоподобные изображения - то есть рассчитанные с учетом кривизны пространства, красного смещения и физических свойств диска могут быть получены для произвольной точки, даже находящейся внутри горизонта событий. Был даже создан фильм, показывающий, как меняются эти искажения при движении по времениподобной траектории вокруг черной дыры (Delesalle, Lachieze-Reyand Luminet, 1993). Рисунок 23 - это один из его кадров для случая движения по навесной параболической траектории. При таком "мысленном путешествии" мы понимаем, что именно видела третья бабочка из рассказанной во введении легенды.
Черные дыры, долгое время рассматриваемые астрономами как никому не нужные теоретические изыски, сейчас повсеместно считаются основным объяснением для массивных рентгеновских двойных и галактических ядер. Помимо того, что они считаются наиболее вероятными моделями, они также и наиболее просты (а согласно принципу простоты, предпочтительной является та модель, которая объясняет явление при наименьшем числе дополнительных предположений). Однако, для того чтобы обрести сегодняшнее повсеместное признание, сами черные дыры вынуждены были существенно измениться, став из "голых", пассивных и абсолютно невидимых объектов наиболее мощным источниками излучения во вселенной.
Список литературы
Begelman, M., Rees, M. (1996): Gravity's Fatal Attraction: Black Holes in the Universe (New York: Scientific American Library) Chandrasekhar, S. (1992): The Mathematical Theory of Black Holes, (Oxford: Oxford University Press) Delesalle, L., Lachièze-Rey , M., Luminet J.-P. (1994): Infinitely Curved, video VHS 52 mn, Arte/CNRS Audiovisuel DeWitt, C., DeWitt, B.S. (Eds.) (1973): Black Holes (Les Houches School, Gordon and Breach: New York) Hawking, S.W., Israel, W. (Eds.) (1989): 300 Years of Gravitation (New York, Cambridge: Cambridge University Press), pp. 199-446 Luminet, J.-P. (1979): Astron. Astrophys. 75, 228 Luminet, J.-P., Carter, B. (1986): Astrophys. J. Suppl. 61, 219 Luminet, J.-P. (1992): Black Holes (New York, Cambridge: Cambridge University Press). German translation: Schwarze Löcher (Vieweg, 1997) Marck, J.-A. (1993): Class. Quantum Grav. 13, 393 Misner, C.W., Thorne, K.S., Wheeler, J.A. (1973): Gravitation (San Francisco: Freeman) O'Neill, B. (1995): The Geometry of Kerr Black Holes (Wellesley: Peters) Wheeler, J.A. (1990): A Journey into Gravity and Spacetime. (New York, Cambridge: Cambridge University Press)Комментарии (7):
Не понимаю:
>"Любой звездный остаток (холодная равновесная конфигурация) с массой, большей примерно
и тут же:
>"На рисунке 19 показаны траектории звезд на диаграмме "масса -- средняя плотность" в соответствии с последними наблюдательными и теоретическими данными. Звезды с массой меньше
Как трактовать разницу в цифрах??
Поправка!!!
При простом копи/паста не отразились числовые значения:
В первом фрагменте "большей примерно 3Мо"
Во втором фрагменте "Звезды с массой меньше 8Мо", "между 8Мо и 45Мо",
"черные дыры образуются только из звезд массивнее 45Мо"
Рассмотрев внимательнее приведённые зднсь рисунки со световыми конусами я пришёл вот к какому интересному выводу. Почему, собственно говоря, замедляется время для стороннего наблюдателя. Это связано с тем, что световые конусы, расположенные около сферы Шварцшильда, разворачиваются и, таким образом, временной промежуток между двумя явлениями, происходящими на объекте, приблежающемся к сфере Шварцшильда для стороннего наблюдателя будет увеличен в силу запаздывания к нему сигнала (и только!). Действительно, при движении объекта в каждое мгновение каждый световой конус будет иметь свой увеличивающийся наклон, который должен быть для стороннего наблюдателя компенсирован. А для этого то же нужно время. Таким образом, и происходит якобы замедление времени: собственное время + время на компенсацию. Но, на самом объекте скорость течения времени такая же, что и для стороннего наблюдателя. Если бы объект действительно остановился у сферы Шварцшильда, то эффект замедления времени бы пропал! Т.к. световые конусы заняли бы строго определённый угол!
Стоит так же отметить, что поворот конусов никак не связан с силой притяжения около сферы Шварцшильда. Так, чёрная дыра порядка 10 триллионов солнечных масс будет иметь притяжение около этой сферы не больше, чем на поверхности Земли. Поэтому гипотетическая ракета в этом случае сможет выйдти за пределы сферы Шварцшильда (световой конус существенен только для свободно движущихся частиц (имеется в виду, что ракета имеет силу тяги двигателей коих у частиц нет)).
Возник вот какой вопрос, касающийся гравитационных волн и гравитонов. Если исходить из расположения световых конусов, то никакая гравитационная волна и никакой гравитон не могут выйдти за пределы сферы Шварцшильда, а нижние гравитоны, расположенные ближе к сингулярности, ну никак не могут воздействовать на верхние гравитоны, тогда как последние могут воздействовать на нижние.Т.е. отсутствует взаимодействие. Получается, что гравитационное поле не может иметь квантовую природу впринципе и никакие гравитоны просто не существуют? Или гравитоны и гравитационные волны имеют скорости распространения равные бесконечности (чтобы покинуть сингулярность)? И даже, если последнее справедливо, то почему гравитоны не превращаются в ничто в отличие от остальных элементарных частиц?
Будучи молодым и впервые столкнувшись с концепцией чёрных дыр, я был потрясён её необычайностью и мощью. Тем более, что она как нельзя лучше соответствовала моей страсти к научной фантастике.
Но увы, к сожалению фантастикой эта концепция и оказалась:
1. Чёрных дыр не существует даже в ОТО, например:
В. В. Киселёв, А. А. Логунов, М. А. Мествиришвили
"Чёрные дыры: предсказание теории или фантазия?" - Физика элементарных частиц и атомного ядра, 2006, т. 37, вып.3
(Приводятся аргументы в пользу того, что чёрные дыры не являются строгим следствием Общей теории относительности)
http://www1.jinr.ru/Pepan/2006-v37/v-37-3/2_rus.html
Лоскутов, Ю. М. "О физической нереализуемости "черных дыр" и возможности существования специфических сверхкомпактных объектов" Вестник Московского университета. Сер. 3, Физика. Астрономия. - 2006. - N 3. - С. 18-23
(Доказано, что физически реализуются лишь такие тела, у которых удвоенная масса 2М материи, заключенной под сферой радиуса Z, не превышает этот радиус. Физической причиной этого является гравитационный дефект массы. При "стягивании" вещества в сколь угодно малую область масса тела тоже становится сколь угодно малой. Исследованы физические характеристики таких объектов. Они могут вносить основной вклад в темную массу Вселенной и должны проявляться в эффекте гравитационного микролинзирования. При определенных условиях они могут создавать источники мощного рентгеновского излучения. Рассмотрена динамика пробных тел, падающих на подобные объекты.)
http://phys.sunmarket.com/rus/research/vmuphys/archive/issues-2006/no3/06-3-18.p...
В. В. Киселёв, А. А. Логунов, М. А. Мествиришвили
"О физической противоречивости решений Шварцшильда и Керра" - Теоретическая и математическая физика, 2010, т. 164, №1
(Метрика нейтральной стационарной "чёрной дыры" не удовлетворяет условиям причинности, сформулированным Гильбертом. Как следствие, пробное тело, свободно падающее, например, во вращающуюся "чёрную дыру", приобретает за конечное время удалённого наблюдателя на поверхности эргосферы скорость, равную скорости света, что приводит к физическому противоречию и указывает на принципиальный недостаток вакуумного решения уравнения Эйнштейна вне источника)
И ещё:
С. С. Герштейн, А. А. Логунов, М. А. Мествиришвили
"Несовместимость законов сохранения числа барионов и электрического заряда с концепцией чёрных дыр"
Доклады Академии Наук т. 439, №2, июль 2011
Этих двух статей пока в Интернете нет.
Но есть вот такая:
С. С. Герштейн, А. А. Логунов, М. А. Мествиришвили
"Массивный пылевой шар, пульсирующий под действием собственного гравитационного поля"
Теоретическая и Математическая Физика, 2008, т. 155, №2
"Согласно РТГ пульсации массивного пылевого шара, как и циклическое развитие однородной и изотропной Вселенной, обязаны своим происхождением общему фундаментальному свойству гравитационного поля – свойству самоограничения. Именно ЭТО СВОЙСТВО ИСКЛЮЧАЕТ БОЛЬШОЙ ВЗРЫВ, вместо него возникает состояние, когда Вселенная имела большую плотность и высокую температуру. Оно также ИСКЛЮЧАЕТ КОЛЛАПС И ЧЁРНЫЕ ДЫРЫ, заменив их наличием во Вселенной физических объектов больших масс.
Необходимо особо отметить, что НЕТ НИ ОДНОГО НАБЛЮДАТЕЛЬНОГО ФАКТА, который бы с необходимостью требовал для своего объяснения предположения о существовании черных дыр – объектов, не имеющих материальной поверхности. Все наблюдательные факты прекрасно объясняются существованием во Вселенной физических объектов больших масс, имеющих материальную поверхность. Именно такие объекты реально существуют во Вселенной. Наличие их следует из РТГ."
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=tmf&paperid=6208&optio....
Последние по времени статьи по РТГ на эту тему:
С. С. Герштейн, А. А. Логунов, М. А. Мествиришвили
"Принцип причинности Гильберта и невозможность гравитационного коллапса нестатического сферического тела" - Доклады Академии Наук т.436, № 4, февраль 2011
(Доказано, что гравитационный коллапс тела невозможен независимо от величины его массы, а следовательно невозможно и безграничное гравитационное сжатие Оппенгеймера)
А. А. Логунов, М. А. Мествиришвили
"Структура интеграла движения и невозможность гравитационного коллапса"
Теоретическая и Математическая Физика, том 171:1 (2012), 150–153
(Доказывается, что гравитационный коллапс невозможен)
Кроме того:
Не может существовать термодинамика того, чего нет. Но тем не менее:
"Основываясь на статистическом подходе, мы увидим, что определяющим свойством энтропии является ВОГНУТОСТЬ. Отсюда следует, что все предлагаемые выражения для энтропии, в которых она полагается пропорциональной квадрату экстенсивной величины, АБСОЛЮТНО БЕССМЫСЛЕННЫ. ЭТО ЗАЧЁРКИВАЕТ ВСЁ ТО, НА ЧЁМ ОСНОВАНА ТЕРМОДИНАМИКА ЧЁРНЫХ ДЫР...
Выражение для "энтропии" чёрной дыры представляет собой всё, что угодно, кроме энтропии".
Б. Лавенда "Статистическая физика. Вероятностный подход" (перевод с английского) М., МИР, 1999 г., стр. 56
То есть, всё то, что Хокинг написал про ИСПАРЕНИЕ ЧЁРНЫХ ДЫР - БЕССМЫСЛИЦА!
Последние по времени статьи по РТГ:
С. С. Герштейн, А. А. Логунов, М. А. Мествиришвили
"Принцип причинности Гильберта и невозможность гравитационного коллапса нестатического сферического тела" - Доклады Академии Наук т.436, № 4, февраль 2011
(Доказано, что гравитационный коллапс тела невозможен независимо от величины его массы, а следовательно невозможно и безграничное гравитационное сжатие Оппенгеймера)
А. А. Логунов, М. А. Мествиришвили
"Структура интеграла движения и невозможность гравитационного коллапса"
Теоретическая и Математическая Физика, том 171:1 (2012), 150–153
(Доказывается, что гравитационный коллапс невозможен)
(РТГ - это Релятивистская теория гравитации, разрабатываемая академиком РАН А. А. Логуновым и его коллегами)
И ещё интересная информация:
"Чёрных дыр не существует?
Учёные из Кливлендского Университета, штат Огайо, вывели математические формулы, из которых следует, что чёрных дыр не существует. Это открытие, оказавшись правильным, произведёт революцию в астрофизике и разрешит парадокс, сбивающий последние четыре десятилетия физиков с толку".
http://newsland.com/news/detail/id/794786/
Оказывается на западе довольно много учёных, отрицающих существование чёрных дыр. Например:
"Quantum Leap: Blackholes Don’t Exist
February 6th, 2010 by Thomas Kennedy"
Despite the regular pronouncements in the popular press, there is a growing debate among physicists that, in fact, the mathematical models that at one time purported to clearly substantiate the existence of such, black holes are proving out to be false...
In and of itself, the hypothesis of black holes has always violated notions of both general and special relativity regarding matter and energy as it applies to the concept of a singularity and an event horizon...
In addition to the violation of both forms of relativity, black holes also violate the theorems of quantum mechanics through the loss of information from our universe to some other location that we don’t know of. In the world of qm, information doesn’t leak out, but is contained in our universe."
http://blog.askyfullofstars.com/2010/02/quantum-leap-blackholes-dont-exist/
Автор указывает на то, что концепция чёрных дыр противоречит и ОТО, и СТО, и квантовой механике
Но, по словам А. А. Логунова, за такое утверждение таких учёных могут лишить финансирования - поэтому большинство сомневающихся молчит
Кто-нибудь сможет прокомментировать вот это: http://www.astronomy.ru/forum/index.php/topic,102355.msg2305169.html#msg2305169
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.






Всё это прекрасно. Но есть одно Но. Все световые конусы рассмотрены при наличии силы гравитации для частиц, не имеющих сил тяги (коеми обладает, скажем, ракета). Если какой-либо объект будет обладать некоторой силой тяги, то он легко сможет пойти не по геодезическим линиям (кривое пространство всегда можно заменить плоским другой размерности). В СТО это невозможно, поскольку там геодезические линии имеют иную природу, не связанную с какими-либо силами.