Теория относительности и квантовая механика открывают мир античастиц
О том, что у частиц имеются двойники — античастицы, широко известно. Менее известно, что эта симметрия природы с необходимостью вытекает из свойств пространства и времени, установленных специальной теорией относительности. Этому вопросу посвящена настоящая статья.
Теория дирака
В 1928 году П.А.М. Дираку удалось объединить две великие теории XX века: квантовую механику и специальную теорию относительности. Дирак нашел уравнение, которое определяет волновую функцию электрона в релятивистской (то есть удовлетворяющей принципам теории относительности) квантовой механике. Решая это уравнение он столкнулся с неожиданным фактом. Оказалось, что наряду с решениями уравнения Дирака, отвечающими электрону, движущемуся с положительной полной энергией, существуют решения с отрицательной полной энергией. Оба этих решения являются разными корнями одного уравнения:
$$\frac{\mathcal{E}^2}{c^2}-\vec{p}^2=m^2c^2,~~~ \mathcal{E}^2=\pm c\sqrt{\vec{p}^2+ m^2c^2}~~~~~~~(1)$$
Уравнению (1) удовлетворяют известные формулы
$$\mathcal{E}=\frac{mc^2}{\sqrt{1-v^2/c^2}},~~~~~p=\frac{mv}{\sqrt{1-v^2/c^2}}$$
где $m$ и$\vec{p}$ — соответственно масса и импульс электрона, а $c$ — скорость света. С физической точки зрения отрицательные энергии недопустимы: частица с отрицательной энергией, сталкиваясь с другой частицей и передавая ей часть своей энергии, должна была бы в этом случае приобретать еще большее по абсолютной величине отрицательное значение энергии. Таким образом, она могла бы разгоняться до сколь угодно больших по абсолютной величине отрицательных значений энергии, совершая бесконечную работу над другими телами. Что делать, если в теории появились решения, отвечающие частицам с отрицательной энергией? Можно было, конечно, подумать, что неверна предложенная теория. Но тогда, в свою очередь, возникал бы вопрос: почему оказалось "неправильным" уравнение, основанное на двух хорошо проверенных к тому времени теориях: квантовой механике и специальной теории относительности? Надо было искать выход из этого противоречия. В классической (неквантовой) механике возможность существования частиц с отрицательной энергией можно было просто игнорировать. Области положительных и отрицательных энергий отделены друг от друга энергетической "щелью" (рис. 1). Поскольку в классической механике энергия частиц меняется непрерывно, скачок частицы из состояния с положительной энергией в состояние с отрицательной просто невозможен. Поэтому достаточно предположить, что все частицы вначале находятся в состояниях с положительными энергиями, чтобы полностью исключить их появление с отрицательными энергиями.
В квантовой механике, однако, нельзя игнорировать состояние с отрицательными энергиями. Прежде всего, потому, что квантовая механика допускает скачки и частицы с положительными энергиями, взаимодействуя с другими, могли бы перескакивать из состояний с положительными энергиями в состояния с отрицательными. Кроме того, выяснилось, что состояния с отрицательными энергиями в действительности нужны, так как только при их учете удается правильно (на основании теории Дирака) описать рассеяние света электронами. Таким образом, складывалось совершенно драматическое положение: с одной стороны, нельзя допустить существование состояний с отрицательными энергиями, а с другой — нельзя их игнорировать.
Соотношения неопределённостей – фундаментальные соотношения квантовой механики, устанавливающие предел точности одновременного определения так называемых дополнительных физических величин, характеризующих систему (например, координаты и импульса). В упрощённой формулировке эти соотношения утверждают, что дополнительные физические величины не могут быть одновременно точно определены. Неопределённостей соотношения являются следствием двойственной, корпускулярно-волновой природы частиц материи, отражением вероятностной (статистической) сути квантовой механики.
Неопределённостей соотношения имеют вид неравенств, например, $\Delta x \Delta p \geq \hbar=\frac{h}{2\pi} $, где $\Delta x $ – неопределённость координаты (частицы или системы), $ \Delta p $ – неопределённость её импульса, а $h= 6.626\ 069\ 57(29)\times10^{-34}$ Дж*с - постоянная Планка. Отсюда видно, что произведение неопределённостей координаты и импульса не может быть меньше $\hbar$, и никаким усовершенствованием методов наблюдения нельзя преодолеть этот рубеж. Увеличение точности определения координаты неизбежно ведёт к потере точности определения импульса. Предельная точность одновременного определения координаты и импульса даётся соотношением $\Delta x \Delta p \approx \hbar .$
Другая важная пара дополнительных физических величин – энергия $Е$ и время $t.$ Соотношение неопределённостей для них имеет вид $\Delta E \Delta t \geq \hbar$. Это соотношение для релятивистских системы или частиц (двигающихся со скоростью близкой к скорости света с) может быть получено из соотношения неопределённостей для координаты и импульса простым преобразованием: $\Delta x/c \Delta pc \geq \hbar=\Delta E \Delta t \geq \hbar$. Полученное соотношение для времени и энергии можно трактовать следующим образом. Для того, чтобы определить энергию частицы (системы) с точностью $\Delta E$, необходимо проводить измерения в течение промежутка времени $ \Delta t \geq \frac{\hbar}{\Delta E}$. Следствием этого соотношения является возможность виртуальных (ненаблюдаемых) процессов, лежащих в основе механизма взаимодействия частиц в квантовой теории поля. Две частицы взаимодействуют, обмениваясь с нарушением баланса энергии на величину $\Delta E$ виртуальным (ненаблюдаемым) переносчиком взаимодействия, существующим в течение времени $ \Delta t \leq \frac{\hbar}{\Delta E}$
Другая трактовка соотношения $\Delta E \Delta t \approx\hbar $ связана с понятием времени жизни нестабильного (распадающегося состояния системы или частицы). Так, если квантовая система в дискретном энергетическом состоянии живёт в среднем время $\tau \approx \Delta t$, то энергетическая ширина уровня $ \Gamma$ даётся соотношением $$ \Gamma \approx \Delta E \approx\frac{\hbar}{\Delta t} \approx\frac{\hbar}{\Delta \tau}. $$
В силу крайней малости константы Планка $\hbar$, соотношения неопределённостей не играют практически никакой роли для макроскопических тел.
Для решения этого противоречия Дирак выдвинул очень смелую (многим казалось, просто безумную) гипотезу. Он предположил, что в вакууме (то есть при отсутствии частиц с положительными энергиями) все состояния с отрицательными энергиями уже заполнены находящимися в них электронами. Тогда, согласно принципу запрета В. Паули, электроны с положительными энергиями не смогут переходить в уже занятые состояния с отрицательными энергиями, и проблема будет решена (Принцип Паули запрещает находиться в одном и том же состоянии двум (или более) одинаковым частицам, имеющим внутренний момент количества движения (спин), равный полуцелому значению постоянной Планка $h$. Такие частицы называются фермионами. К ним, в частности, относятся электроны и протоны, имеющие спин $h/2.$) .
Безумие идеи Дирака заключалось в том, что вакууму при этом приписывался бесконечный отрицательный заряд от бесконечного числа существующих в нем электронов с отрицательными энергиями. Дирака это обстоятельство не очень смущало, так как он предложил считать, что все наблюдаемые явления происходят на фоне именно такого заполненного вакуума. Независимо от того, можно ли было идею Дирака считать безумной или нет, надо было рассмотреть различные следствия из этой идеи и сравнить их с существующими опытными данными, чтобы выяснить, не противоречит ли эта идея каким-то уже известным опытам, или, быть может, она предсказывает новые неизвестные явления, которые можно обнаружить экспериментально. (Именно таким подходом к безумным идеям отличается истинная наука от лженауки и прожектерства.) Прямым следствием гипотезы Дирака было следующее.
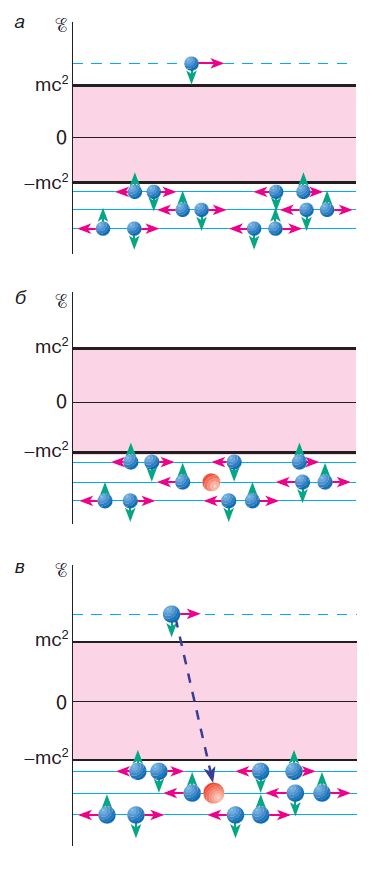
Рис. 1. а - электрон в вакууме Дирака. Все состояния с отрицательной энергией заняты. Импульсы частиц (горизонтальные красные стрелки) и проекции спинов (зеленые вертикальные стрелки) в вакууме скомпенсированы. Электрон с положительной энергией не может перейти в занятые состояния с отрицательной энергией; б - дырка в вакууме Дирака. Система имеет по отношению к заполненному вакууму положительную энергию, заряд $(-е),$ импульс $(-\tilde{р})$ и проекцию спина $(-s_z)$, то есть дырка ведет себя как частица с положительной энергией и противоположным зарядом ("позитрон"); в - электрон и дырка. Возможен переход электрона в состояние с отрицательной энергией, то есть аннигиляция электрона и позитрона
Допустим, что в заполненном дираковском вакууме (или, как говорят, в дираковском подвале (см. рис. 1, б)) исчез каким-то образом один электрон с отрицательной энергией. Образовавшееся тогда состояние (с дыркой в заполненном вакууме) приобретет по отношению к вакууму положительную энергию и положительный заряд (так как исчез электрон с отрицательной энергией и отрицательным зарядом). Это состояние будет также обладать по отношению к вакууму импульсом и проекцией момента (спина), противоположными исчезнувшему электрону (поскольку в заполненном вакууме импульс и спин исчезнувшего электрона компенсировались импульсом и спином других электронов). Другими словами, образовавшаяся дырка будет вести себя по отношению к дираковскому вакууму как частица с положительным зарядом и энергией. В первый момент, когда было получено это следствие, Дирак даже обрадовался, так как подумал, что дырка с положительным зарядом может быть протоном и, таким образом, его теория объясняет существование протона в качестве дырки в вакууме (напомним, что в то время известны были только две элементарные частицы: электрон и протон). Однако вскоре было показано, что, исходя из теории Дирака, дырка обязательно должна иметь ту же самую массу, что и электрон. Такой частицы (позитрона) в то время на опыте не наблюдали. Сомнения в правильности теории Дирака еще более усилились, когда выяснилось, что теория предсказывает совершенно необычное поведение дырки по отношению к электрону с положительной энергией. Действительно, если в вакууме имеется дырка (то есть незаполненное состояние с отрицательной энергией), то ничто не запрещает электрону с положительной энергией перейти в это состояние и заполнить дырку, передав выделяющуюся энергию на излучение $\gamma$-квантов (см. рис. 1, в). В результате электрон и позитрон взаимно уничтожаются — аннигилируют.
Были получены и другие совершенно необычные для современников следствия теории Дирака. Сомнения в справедливости теории исчезли после открытия позитрона, обнаружения процессов рождения электрон-позитронных пар и аннигиляции электрона с позитроном. Что же касается безумного дираковского вакуума с бесконечным зарядом, то более углубленное развитие теории позволило вовсе отказаться от него, сохранив основное следствие: исчезновение частицы с отрицательной энергией равносильно появлению античастицы с противоположным зарядом и положительной энергией, обладающей при этом импульсом и спином, противоположными исчезнувшей частице. Выяснилось, что существование античастиц и поразительная симметрия между движением частиц и античастиц являются прямыми следствиями специальной теории относительности и квантовой механики. Поэтому неудивительно, что теория Дирака, основанная на этих принципах, привела к открытию античастиц. Строгое доказательство этого требует привлечения специальных знаний, относящихся к квантовой теории поля. Постараемся, однако, дать упрощенную иллюстрацию, позволяющую пояснить, каким образом, исходя из свойств пространства и времени, можно прийти к идее о необходимости существования античастиц.
Пространство минковского и его симметрия
Суть теории относительности в том, что наше трехмерное пространство образует вместе со временем единую и неразделимую сущность — четырехмерное пространство (так называемое пространство Минковского), в котором мерой удаленности двух событий друг от друга служит величина $\Delta s$, называемая интервалом между событиями. Квадрат интервала в инерциальной системе координат $$(\Delta s)^2 = c^2(\Delta t)^2 – (\Delta x^2+\Delta y^2+\Delta z^2), $$ где $\Delta t , \Delta x, \Delta y, \Delta z -$ разности времен и декартовых координат двух событий, происходящих соответственно в двух пространственно-временных точках пространства Минковского $(t_1 , x_1, y_1, z_1)$ и $(t_2, x_2, y_2, z_2),$ так что $\Delta t =t_2-t_1, \Delta x =x_2-x_1$,и т.д.
Интервал между двумя событиями остается одинаковым, даже если они наблюдаются в разных системах отсчета, движущихся равномерно и прямолинейно относительно друг друга (хотя разности времен и пространственных расстояний между этими событиями в разных системах отсчета будут разными). Именно поэтому интервал и служит объективной (не зависящей от выбранной системы отсчета) мерой "удаленности" событий или, можно сказать, расстоянием между событиями в пространстве Минковского. Переход же от одной системы отсчета к другой представляет поворот в пространстве Минковского, при котором интервал между событиями (то есть "расстояние") не меняется. (Если одна система отсчета движется, например, вдоль направления оси х другой системы, то переход от одной системы к другой представляет поворот в плоскости $(x,t)$ пространства Минковского.) Поскольку, согласно принципу относительности, все физические законы в обеих системах отсчета одинаковы, можно сказать, что они остаются неизменными (инвариантными) при поворотах в пространстве Минковского.
Наряду с поворотами в пространстве Минковского можно рассматривать так называемые дискретные преобразования: инверсию пространственных координат и обращения времени, то есть замену пространственных координат и времени событий на противоположные им значения: $x\rightarrow-x;~y \rightarrow –y;~z\rightarrow –z.$ Какой смысл имеют эти преобразования? Замена одной из пространственных координат, скажем $z\rightarrow –z$, (при сохранении всех остальных), означает, что наряду с рассматриваемым событием мы рассматриваем его зеркальное изображение относительно плоскости, перпендикулярной оси$z$ (то есть плоскости $ху$). Отражение всех пространственных координат представляет отражение в трех взаимно перпендикулярных плоскостях. Очевидно, что при таких отражениях скорости частиц (значит, и импульсы) меняются на противоположные.
Что означает формальная операция обращения времени $t\rightarrow –t ?$ Нетрудно понять, что и ей можно придать простой физический смысл. Он состоит в том, что наряду с реально существующим в природе движением рассматривается движение, обращенное во времени, то есть такое, в котором система проходит все ранее пройденные состояния в обратном порядке с противоположными скоростями. Обращенное по времени движение можно непосредственно наблюдать запустив видеофильм в обратном направлении. Подчеркнем, что обращенное по времени движение может в некоторых случаях действительно осуществляться в природе (тогда говорят, что оно обратимо по времени), а может и не осуществляться, быть некоторой фикцией. Это легко видеть при демонстрации в обратном направлении видеофильма с движением камня, брошенного вверх в поле земного тяготения. Если не учитывать сопротивления воздуха, то, изменив на какой-либо высоте скорость камня на противоположную, мы получим реально существующее движение падающего к Земле камня, обращенное по времени относительно брошенного вверх.
То же самое замечание надо сделать и к предыдущему рассмотрению зеркального отражения. Объект, получающийся благодаря зеркальному отражению реального предмета, может иногда реально существовать в природе, а иногда и не существовать. Так, в зеркальном изображении человека получается объект с сердцем в правой стороне груди. Такие люди если и встречаются в жизни, то только как очень редкая аномалия. Аналогичным образом зеркальным изображением винта с правой нарезкой будет винт с левой нарезкой. Такие винты, конечно, можно изготовить. Но изготавливаются они довольно редко. Если бы они вообще никогда не изготовлялись, то можно было бы сказать, что зеркальная симметрия для правых винтов нарушается максимальным образом: объект, полученный в результате зеркального изображения правого винта, вообще не существует.
Заметим теперь, что в нашем обычном трехмерном пространстве (с геометрией Евклида) четное число зеркальных отражений какого-либо объекта в различных плоскостях приводит к изображению, которое можно совместить с изображаемым объектом путем вращения в пространстве. Это иллюстрируется рис. 2.

Рис. 2. Если зеркальное изображение левой руки 1 относительно оси $Y$ представляет правую руку 2, которую путем вращения в плоскости $XY$ нельзя совместить с левой, то зеркальное изображение правой руки 2 относительно оси $X$ вновь представляет левую руку 3, которая может быть совмещена с 1 путем поворота в той же плоскости.
Точно также инверсия всех трех пространственных координат и времени математически может быть представлена как поворот в пространстве Минковского на некоторый (правда, мнимый) угол. Если теперь вспомнить, что, согласно теории относительности, все явления природы инвариантны относительно поворотов в пространстве Минковского, то можно заключить, что все законы природы должны быть симметричны относительно одновременной инверсии всех пространственных координат и обращения времени. (Первая из этих операций обозначается символом Р, а вторая — Т.) Таким образом, (PT)-симметрия должна точно соблюдаться даже в случаях, когда по отдельности не существует зеркальной симметрии (Р) или обратимости процесса по времени (T).
Посмотрим теперь, как должны изменяться энергия и импульс частиц при (РT)-преобразовании. Согласно теории относительности, энергия и импульс частицы составляют вместе так называемый 4-вектор $\frac{\mathcal{E}}{c},p_x,p_y,p_z$ который при преобразованиях в пространстве Минковского преобразуется точно также, как временная и пространственные координаты частиц $(ct, х, у, z).$ Это означает, что при (РТ)-преобразовании импульс и энергия частицы должны менять свой знак, то есть законы природы, согласно теории относительности, должны быть симметричны относительно частиц с положительными и отрицательными энергиями. Это общее рассуждение объясняет, почему уравнение Дирака дает решения как с положительными, так и с отрицательными энергиями частиц.
Но как же быть с отрицательными энергиями? Ведь мы убедились ранее, что они физически недопустимы. И тут на помощь приходит квантовое описание движений частиц, позволяющее изгнать отрицательные энергии ценой введения античастиц.
Квантово-полевое описание движения
Пусть частица с положительной энергией $\mathcal{E}>0$ переходит из какого-то состояния 1 в состояние 2. (Символически это изображено на рис. 3, а стрелкой.) Согласно квантово-механическому описанию, это можно представить как исчезновение частицы в состоянии 1 и ее появление в состоянии 2. При этом в точке 1 происходит потеря энергии$\Delta \mathcal{E}=- \mathcal{E}<0$ (поскольку в ней исчезает частица с положительной энергией), а в точке 2 приобретается энергия$\Delta \mathcal{E}=\mathcal{E}>0$ (поскольку вновь появилась частица с положительной энергией). Таким образом, закон сохранения энергии оказывается ненарушенным. Аналогичный переход между состояниями 1' и 2' для частицы с отрицательной энергией $\mathcal{E}'<0$ сопровождался бы приобретением положительной энергии в 1' и потерей ее в 2'. Сравнивая теперь на рис. 3, а, б оба случая движения можно заметить, что переход частицы с отрицательной энергией из одного состояния в другое выглядит так, как если бы частица с положительной энергией совершила обратный переход, то есть переходила бы из состояния 2' в 1'.
Таким образом, кажется, что можно представить процессы с частицами отрицательных энергий как обращенные по времени процессы с частицами положительных энергий. И это действительно так, если речь идет об абсолютно нейтральных частицах, не имеющих заряда. Но в нашем рассмотрении мы упустили, что частица может обладать каким-то сохраняющимся зарядом (например, электрическим $q$). В этом случае изменение заряда в состояниях, где исчезают или рождаются частицы с положительными и отрицательными энергиями, одинаково. Поэтому, например, исчезновение в состоянии 1' частицы с отрицательной энергией нельзя уже трактовать как рождение такой же частицы с положительной энергией и тем же самым зарядом (по скольку при этом должно было бы быть изменение заряда $\Delta q =q $, а не $\Delta q =-q$). Это должно быть рождение частицы с противоположным зарядом (но, конечно, с той же массой и спином, то есть античастицы). Таким образом, для изгнания состояний с отрицательными энергиями необходимо предположить, что каждая заряженная частица имеет двойника — античастицу.
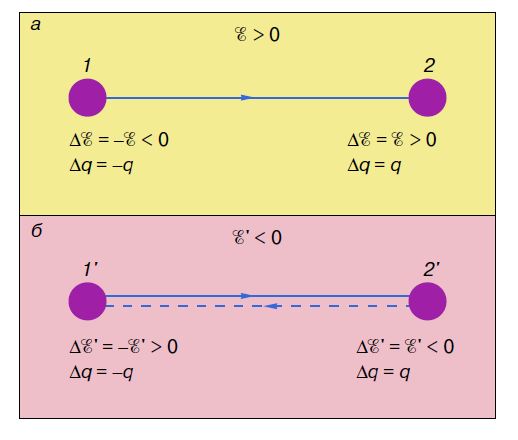
Рис. 3. Соотношение неопределенности Гейзенберга рассматривается как закономерность, не поддающаяся нашим представлениям о реальности. Между тем при отказе от связи соотношения с волновой функцией и ее "вероятностной интерпретацией" обоснование соотношения становится простым и очевидным. Исходим из положений, что при использовании этого соотношения измеряется действие, кратное h — постоянной Планка и, если действие определяется сопряженными параметрами. то измерение каждого из них в отдельности невозможно. В этом случае точность измерения принципиально не может превосходить значения h. Измерение каждого параметра связано с соответствующей "градуировкой" мерительного инструмента. При оценке точности измерения сопряженных параметров их измерение должно происходить не просто одновременно, а путем единого измерения. В этом случае, например, "парадокс Эйнштейна – Подольского – Розена" теряет смысл. Воздействие мерительного инструмента на результат измерения не является спецификой микромира и, соответственно, квантовой механики.
Тогда движение частиц с отрицательной энергией можно представить как обращенное по времени зеркальное изображение движения соответствующих им античастиц с положительной энергией. При такой трактовке выполняется правило Дирака: исчезновению частицы с отрицательной энергией соответствует рождение античастицы с положительной энергией и, наоборот, рождению такой частицы с отрицательной энергией — исчезновение ее античастицы. При этом, однако, вовсе не требуется существования заполненного частицами вакуума Дирака с бесконечным зарядом. Вакуумом будет состояние, в котором отсутствуют какие-либо частицы или античастицы. Вопрос, какую частицу называть частицей, а какую — античастицей, становится условным и является предметом соглашения. Мы будем обозначать античастицу значком ~ над символом частицы.
Античастицы должны существовать не только у частиц с электрическим зарядом. Они должны быть также и у электрически нейтральных частиц, если эти частицы имеют какую-то сохраняющуюся во всех процессах внутреннюю характеристику. Например, как показывает опыт, при любых превращениях сохраняется суммарное число тяжелых частиц — барионов, к которым относятся нуклоны: нейтрон и протон.
Можно считать поэтому, что нейтрон обладает определенным сохраняющимся барионным зарядом В (его можно условно принять за единицу: $B = 1$), а это означает, что у нейтрона должна быть античастица — антинейтрон с барионным зарядом, равным -1.
Таким образом, благодаря свойствам пространства- времени, установленным теорией относительности, в природе существует удивительная симметрия, а именно любому движению каких-либо частиц, происходящему в природе, можно сопоставить симметричное ему движение их античастиц, которое также может реально осуществляться в природе и выглядит как отраженное в зеркале и обращенное по времени движение частиц. Это утверждение называют $CPT-$теоремой.Под С здесь принимается операция перехода к античастицам. Ее называют зарядовым сопряжением.
Приведенные рассуждения, конечно, не являются строгим доказательством $CPT-$ теоремы. В частности, требует доказательства предположение о том, что законы взаимодействия любых частиц не меняются при поворотах в пространстве Минковского на мнимые углы.
Исследование этого вопроса требует довольно тонких математических методов и связано с дополнительными предположениями. Поэтому независимо от теоретического рассмотрения проводилась и будет в дальнейшем проводиться все более точная экспериментальная проверка $CPT-$симметрии. Требуемое ею равенство масс частиц и античастиц проверено для электрона и позитрона с точностью $0.9\cdot 10^{-8}$ их величины. Уникальную возможность проверки $CPT-$симметрии (по причинам, на которых не можем здесь останавливаться) дают так называемые $K^0$ и $\tilde{K^0}$-мезоны, равенство масс которых установлено сейчас с точностью $0.9\cdot 10^{-20}. $ Проверены и другие следствия $CPT-$симметрии: равенство времени жизни нестабильных частиц и античастиц и равенство (по абсолютной величине) их магнитных моментов. Первое проверено для мюонов с точностью $8\cdot 10^{-5},$ а второе — для электронов и позитронов с точностью $2\cdot 10^{-12}. $
На ускорителе в Брукхэйвене (США) удалось обнаружить ядра антидейтерия, состоящие из антипротона и антинейтрона: $\tilde{d}(\tilde{p},\tilde{n})$ а на Серпуховском ускорителе в Протвино — даже ядра антигелия-три и антитрития, состоящие из трех антинуклонов: ${}^3\tilde{He}(2\tilde{p},\tilde{n})$ и $\tilde{t}(\tilde{p},2\tilde{n}).$ Для образования антиядер необходимо, чтобы при столкновении протона с обычным ядром родилось несколько антинуклонов, которые затем слиплись бы в антиядра. Вероятность таких процессов очень мала: ядро d рождается одно на $10^6$ столкновений, а ${}^3\tilde{He}$ и $\tilde{t}$ — на $10^{11}.$ В 1996 году в Европейском центре по физике высоких энергий (ЦЕРН) удалось зарегистрировать антиатомы водорода $\tilde{H}$ из антипротона и позитрона. Эти данные подтверждают наши представления о возможности существования антивещества.
Связь процессов между частицами и античастицами
Связь между рождением и исчезновением частиц и их античастиц приводит к тому, что взаимодействие, вызывающее какую-либо реакцию между частицами, неизбежно должно вызывать аналогичные реакции с их античастицами. Так, если существует взаимодействие, приводящее к реакции $a+b \to c+d,$ в котором частицы "а" и "Ь" превращаются в "с" и "d", то это же взаимодействие должно приводить, например, и к реакции $\tilde{c}+b \to \tilde{a}+d,$ (поскольку волновые поля частиц "а" и "с" описывают не только возможность исчезновения частицы "а" и рождения "с", но одновременно и возможность рождения а и исчезновения с ). Если учесть, что, согласно законам квантовой механики, взаимодействие, вызывающее реакцию $a+b\to c+d,$ должно вызывать и обратную реакцию $c+d\to a+d$ то мы приходим к простому правилу: взаимодействие, вызывающее реакцию
$a+b \to c+d,$ способно вызывать и все другие реакции, запись которых получается из первой путем переноса символов частиц из одной стороны в другую (с одновременным изменением их на античастицы), а также путем изменения направления стрелки. Очевидно, что это правило аналогично правилу переноса членов алгебраического равенства из одной стороны в другую с одновременной заменой знаков.
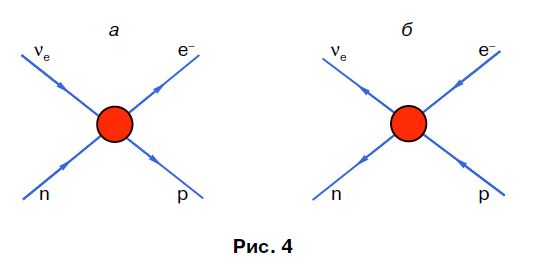
Рис. 4.
Ему можно придать наглядный графический смысл, изобразив движение частиц стрелками и помня, что движение античастиц является обращенным (или, говорят, попятным) во времени, то есть происходит в направлениях, противоположных стрелкам. Так, графики на рис. 4 описывают одновременно несколько процессов: $\beta^-$ и $\beta^+$ распады ($n\to p+e^-+\tilde{\nu}_e$ и $p\to n+e^+ +{\nu}_e$, нейтринные реакции $({\nu}_e +n\to p+e^-$ и $\tilde{\nu}_e+p\to n+e^+),$ так называемый К-захват $(e^-+p\to n+{\nu}_e)$ и др.
Полностью ли симметричны вещество и антивещество? Проблема барионной асимметрии Вселенной
Из общих принципов теории относительности и квантовой механики, как было показано, вытекает симметрия законов природы относительно одновременного проведения трех преобразований $CPT$, но не относительно каждого из них в отдельности. Тем не менее оказалось, что процессы, протекающие в результате электромагнитных и сильных (ядерных) взаимодействий, обладают симметрией относительно каждого из них. Они не меняются при зарядовом сопряжении (С), то есть при замене всех частиц на античастицы. Для любого из них в природе осуществляются зеркально-симметричные (P) и обращенные по времени процессы (Т). В процессах же слабого взаимодействия зеркальная симметрия отсутствует. Так, спин электронов в $\beta-$распаде ядер направлен в основном против направления их импульса. Среднее значение косинуса угла между направлениями спина и импульса $\beta-$электронов равно $v_e/c$, где $v_e$ — скорость электронов. При энергиях электронов $\mathcal{E}\gg m_e c^2$ это значение близко к -1, то есть если представить спины электронов винтами с левой и правой нарезкой, то большая часть электронов вылетает в виде левого винта.
Для антинейтрино в $\beta-$распаде соответствующая величина равна $+v_e/c$, и если антинейтрино имеет нулевую массу покоя (то есть движется всегда со скоростью света), то возможно, что в природе оно встречается только в виде правого винта. Одновременно с нарушением зеркальной симметрии (Р) в процессах слабого взаимодействия нарушается и зарядовая симметрия (С). Вместе с тем в соответствии с гипотезой, высказанной Л.Д. Ландау и независимо Т.Д. Ли и Ц.Н. Янгом, в слабых взаимодействиях сохраняется комбинированная симметрия относительно одновременного преобразования СР. Процессы слабого взаимодействия, происходящие с античастицами, выглядят при этом в точности как зеркальное изображение процессов, происходящих с соответствующими частицами, и симметрия между веществом и антивеществом полностью сохраняется. (В соответствии с СТ-симметрией позитроны в ($\beta^+$-распаде вылетают в основном в виде правого винта, а нейтрино — в виде левого.)
Нарушают $CP$-симметрию особые силы, проявление которых, замеченное пока только в распадах, так называемых долгоживущих $K^0_L-$мезонов (долгоживущие $K^0_L$ и короткоживущие $K^0_s-$ мезоны представляют суперпозицию упомянутых выше в тексте $K^0$ - и $\tilde{K}^0$-мезонов). Природа этих сил пока не установлена и интенсивно изучается. Важное значение для ее раскрытия будут иметь эксперименты по изучению распадов так называемых В-мезонов, содержащих тяжелые Ь-кварки. Такие исследования подготавливаются на будущих коллайдерах (ускорителях со встречными пучками частиц) в ЦЕРНе и США. Нарушение СТ-симметрии в распадах $K^0_L$-мезонов происходит на уровне $2\cdot10^{-3}$ от их распадов по слабому взаимодействию. Но не исключено, что силы, вызывающие нарушение CP-симметрии, значительно меньше и величина их составляет всего $10^{-9}$ от величины слабых взаимодействий. (В распадах $K^0_L$ существует особый механизм усиления таких сверхслабых взаимодействий.)
Силы, нарушающие СТ-симметрию, нарушают тем самым симметрию между веществом и антивеществом. Возможно, что именно они (по мысли, высказанной впервые А.Д. Сахаровым) и привели к барионной асимметрии нашей Вселенной, то есть к тому, что в ней не обнаружено областей из антивещества. Для возникновения асимметрии необходимо, чтобы помимо СР- нарушающих сил происходило нарушение законов сохранения барионного и, по-видимому, лептонного зарядов (которые, согласно современным представлениям, являются лишь приближенными, а не точными законами). Тогда на ранних стадиях расширяющейся Вселенной может возникнуть некоторый небольшой избыток барионов, который сохранится после того, как проаннигилирует основная часть вещества и антивещества, присутствовавшая в горячей Вселенной. Из этого оставшегося избытка и состоит наша Вселенная. Косвенно в пользу такого сценария свидетельствует наблюдаемое сейчас отношение числа барионов к числу фотонов так называемого реликтового излучения (оставшегося от горячей фазы Вселенной). Оно составляет сейчас $10^{-9}$, тогда как в очень горячей фазе Вселенной число барионов, антибарионов и фотонов должно было быть приблизительно одинаковым.
Проблема барионной асимметрии Вселенной — тема особого разговора. О ней упомянули здесь лишь в контексте симметрии между веществом и антивеществом, чтобы показать, как смыкаются воедино самые разные и наиболее актуальные направления исследований физики элементарных частиц и космологии: 1) изучение сил, нарушающих СР- симметрию; 2) поиск нестабильности протонов (несохранение барионного числа); 3) поиск осцилляций нейтрино (в том числе испускаемых Солнцем и обусловленных несохранением лептонного числа); 4) исследования по гамма-астрономии, способные дать сведения о присутствии антивещества во Вселенной; 5) прямой поиск ядер антивещества в космосе с помощью космических аппаратов и др. Исключительно важен поиск так называемых частиц Хиггса, которые, с одной стороны, согласно современным представлениям, необходимы, чтобы известные элементарные частицы приобрели массу, а с другой — могут оказать решающее влияние на динамику расширения Вселенной на ранних ее стадиях. Для поиска частиц Хиггса в ЦЕРНе при участии многих стран (в том числе и России) предлагается соорудить к 2005 году Большой Адронный Коллайдер (Large Hadron Collider — LHC) со встречными пучками протонов, каждый из которых должен иметь энергию ~8 ТэВ (8000 ГэВ). Такая возможность неожиданного объединения самых разных областей знания (от законов микромира до законов, управляющих эволюцией Вселенной) является одной из замечательных и увлекательных особенностей науки.
С. С. ГЕРШТЕЙН
Московский физико-технический институт, Долгопрудный Московской обл.
Нет комментариев.
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.






