СУПЕРЧИСЛА в теории струн
Забытая числовая система, открытая еще в XIX столетний, способна дать простейшее объяснение того, почему наша Вселенная может иметь десять измерений. Еще в школе мы получили базовые знания о числах. Натуральные, рациональные, иррациональные, действительные числа и основные алгебраические операции над ними: сложение, вычитание, умножение и деление - чего же еще? Тем не менее, математикам известно, что числовая система, которую мы изучаем в школе, т.е. множество действительных чисел, - лишь одна из возможных. Более того, другие системы зачастую оказываются полезнее для различных геометрических или физических приложений. Одну из самых необычных альтернатив представляют собой октонионы (или октавы). Забытые почти сразу после открытия в 1843 г., за последние несколько десятилетий они вновь набрали популярность благодаря теории струн. Кроме того, если теория струн верна, то эти числа помогут объяснить, почему Вселенная имеет определенное количество измерений.

Другие числа
Октонионы - далеко не первое изобретение чистой математики, которое стало впоследствии использоваться в различных прикладных науках. Эти числа не были и первой альтернативой классической модели, применявшейся в приложениях. Все началось с действительных чисел, которые изучаются сегодня в школах. Известно, что множество всех действительных чисел можно описать при помощи числовой оси, следовательно, данное множество одномерно. На это можно посмотреть и с другой стороны: поскольку каждой точке прямой можно поставить в соответствие некоторое действительное число, прямая имеет размерность один.
Если теория струн верна, то октонионы смогут объяснить, почему наша Вселенная должна иметь размерность десять
До начала XVI в. никаких других чисел, кроме действительных, известно не было. Уже в эпоху Возрождения математики столкнулись с более сложными уравнениями, которые невозможно было решить, используя только действительные числа. В этой ситуации квадратный корень из -1 стал своеобразным секретным оружием, изобретенным итальянским математиком, инженером, физиком, медиком и астрологом Джероламо Кардано. Если ранее математики, сталкиваясь с невозможностью решить те или иные уравнения, вынуждены были прекратить вычисления, то Кардано позволил себе ввести это мистическое в то время обозначение, включив его в свои вычисления, результатами которых все равно становились действительные числа. Несмотря на то, что средневековый ученый, возможно, и сам до конца не понимал суть сделанного им открытия, ответы он получал правильные. В 1545 г. Кардано опубликовал свои идеи в знаменитом труде «Великое искусство, или об алгебраических правилах». С этого и начались споры о том, существует ли действительно квадратный корень из -1, или это не более чем трюк для вычисления квадратных корней и кубических уравнений. Невзирая на то, что с этими числом было связано множество суеверий и мистических представлений, такие известные математики, как Готфрид Лейбниц, Абрахам де Муавр, Леонард Эйлер, Жан Д'Аламбер, Карл Гаусс, продолжали развивать теорию чисел вида а + ib, где i - квадратный корень из -1, а а и b - действительные числа, которые соответственно называются действительной и мнимой частями комплексного числа.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
- Помимо известных всем действительных чисел существует множество других числовых систем (например комплексные числа), оперирующих с квадратным корнем из -1.
- При желании можно создавать числовые системы более высокой размерности, но при этом для них необходимо определить четыре основные математические операции.
- Одна из таких систем - восьмимерная система октонионов, открытая еще в 1840-х гг., но так и не нашедшая применения за последовавшие 150 лет.
- Сегодня математики считают, что октонионы могут оказаться полезными для различных областей физики элементарных частиц, например для теории струн и теории суперсимметрии.
Геометрическую интерпретацию таких комплексных чисел дали независимо друг от друга Каспер Вессель и Жан Робер Арган. Ее суть заключается в том, что комплексному числу ставится в соответствие точка на плоскости с координатами а по оси х и b по оси у. Аргану также принадлежит идея о том, что четыре основные алгебраические операции с этими числами можно представить как геометрические преобразования на комплексной плоскости. Чтобы лучше понять, в чем дело, приведем пример из области действительных чисел. Сложение и вычитание двух действительных чисел геометрически соответствует сдвигу оси влево или вправо. Умножению и делению соответствует сжатие и растяжение числовой оси. Визуально можно представить себе, что, например, умножение или деление на число 2 «раздвигает» или «сужает» точки оси в два раза соответственно, а умножение на -1 поворачивает ось на 180°.
Аналогичным образом можно представить себе операции с комплексными числами. Тем не менее, здесь есть несколько особенностей. Сложение и вычитание двух комплексных чисел по-прежнему соответствуют сдвигу. Однако на этот раз сдвиг первой точки происходит по двум осям на величины, равные действительной и мнимой частям второго числа соответственно. Подобный сдвиг легче всего описать с точки зрения правил сложения векторов. Что же касается умножения и деления, то с геометрической точки зрения эти операции соответствуют не только сжатию и растяжению, как в случае с действительными числами, но также и повороту на определенный угол. Например, умножение на число i соответствует повороту на 90° против часовой стрелки. Нетрудно заметить, что повторное умножение на число i приведет к еще одному повороту на 90°, что будет соответствовать умножению исходного числа на -1.
С ТОЧКИ ЗРЕНИЯ ГЕОМЕТРИИ
В школе нас учили сопоставлять абстрактные математические операции с конкретными действиями, например с перемещением чисел вдоль числовой оси влево или вправо. Подобная связь между алгеброй и геометрией оказывается очень полезной. Благодаря такому подходу математики могут использовать алгебру октонионов в восьмимерном пространстве, которое с трудом поддается визуализации. На диаграммах внизу показано, как можно визуализировать основные алгебраические операции для действительных и комплексных чисел
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
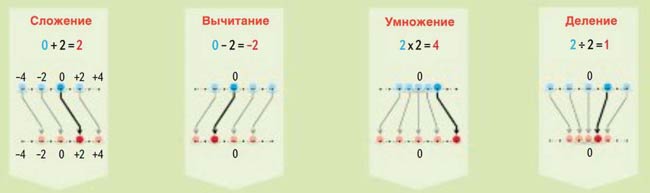
| С геометрической точки зрения прибавление некоторого числа означает сдвиг оси вправо на это число | Вычитание аналогично сложению, но сдвиг оси происходит влево | Умножение растягивает числовую ось в соответствующее число раз | Деление аналогично умножению, но в данном случае происходит сжатие числовой оси |
КОМПЛЕКСНЫЕ ЧИСЛА
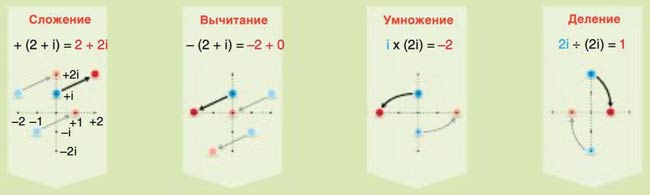
| С геометрической точки зрения комплексное число - это вектор, а потому сложение осуществляется по правилу сложения векторов. С алгебраической точки зрения происходит сложение действительных и мнимых частей чисел | Вычитание аналогично сложению, и его можно представить как сложение первого вектора и второго с обратным знаком | Умножение комплексных чисел заключается в растяжении и в повороте комплексной плоскости против часовой стрелки. Например, умножение на i есть поворот на 90° | Соответственно, операция деления есть сжатие и поворот комплексной плоскости по часовой стрелке |
Таким образом, все операции, введенные для действительных чисел, определены и для комплексных чисел. Фактически использование комплексных чисел расширяет наши возможности и позволяет, например, решать уравнения, не имеющие действительных корней. В таком случае логично предположить, что комплексные числа, а точнее комплексная плоскость - не предел, и возможно построить числовую систему, соответствующую пространству с большим количеством измерений. Тем не менее, подобное расширение было разработано только десятилетия спустя, а о возможном применении такой числовой системы заговорили уже в наши дни.
Открытие Гамильтона
В 1835 г. в возрасте 30 лет математик и физик Уильям Роуан Гамильтон разработал новый способ представления комплексных чисел, которые до него, следуя Аргану, записывали исключительно как а + ib. Выдающийся ирландский математик обратил внимание на то, что комплексное число однозначно представляется парой действительных чисел, которую можно записать в виде (а, b). Он доказал, что если комплексными числами считать такие пары и определить для них основные арифметические операции, это не будет противоречить геометрической интерпретации Аргана. Но Гамильтон не только разработал алгебраическую систему комплексных чисел, но и долгое время исследовал возможности ее расширения до алгебры троек действительных чисел. Предполагалось, что эта алгебра должна была оказаться полезной при решении пространственных задач математической физики, но он потерпел неудачу. Гамильтон даже вспоминал, что одно время, когда он каждое утро спускался к завтраку, его маленький сын неизменно спрашивал, удалось ли ему, наконец, перемножить его тройки. В ответ отец только качал головой и вынужден был признать, что для этих чисел он определил только сложение и вычитание. На тот момент он не знал, что задача, которую он себе поставил, неразрешима.
 Дело в том, что Гамильтон пытался создать числовую систему размерности три, где были бы определены операции сложения, вычитания, умножения и деления, т.е. алгебру. Вообще, алгеброй или алгебраической системой называется некоторое множество (в данном случае числовое) и операции над ним. В 1958 г. было доказано, что любая алгебра, в которой определена операция деления, может иметь размерность один (действительные числа), два (комплексные числа), четыре или восемь. Гамильтон, тем не менее, смог найти решение своей проблемы. 16 октября 1843 г. на пути в Ирландскую королевскую академию в Дублине, проходя вдоль Королевского канала, он вдруг понял, что в трехмерном пространстве повороты, сжатия и растяжения нельзя описать только тремя числами. Ему понадобились четыре числа, определяющие тем самым четырехмерное пространство. Элементы этого пространства - кватернионы - можно записать в виде а + bi + cj + dk, где a, b, с и d - вещественные числа, a i,j и к - квадратные корни из -1. Гамильтон позже написал: «В тот момент в моей голове словно появился гальванический элемент, создавший электрические разряды мыслей. Именно они и привели меня к тем фундаментальным соотношениям между i,j и к, которыми я пользуюсь до сих пор». Он даже высек эти соотношения на мосту Брум-Бридж, и этот замечательный акт математического вандализма был впоследствии увековечен памятной табличкой.
Дело в том, что Гамильтон пытался создать числовую систему размерности три, где были бы определены операции сложения, вычитания, умножения и деления, т.е. алгебру. Вообще, алгеброй или алгебраической системой называется некоторое множество (в данном случае числовое) и операции над ним. В 1958 г. было доказано, что любая алгебра, в которой определена операция деления, может иметь размерность один (действительные числа), два (комплексные числа), четыре или восемь. Гамильтон, тем не менее, смог найти решение своей проблемы. 16 октября 1843 г. на пути в Ирландскую королевскую академию в Дублине, проходя вдоль Королевского канала, он вдруг понял, что в трехмерном пространстве повороты, сжатия и растяжения нельзя описать только тремя числами. Ему понадобились четыре числа, определяющие тем самым четырехмерное пространство. Элементы этого пространства - кватернионы - можно записать в виде а + bi + cj + dk, где a, b, с и d - вещественные числа, a i,j и к - квадратные корни из -1. Гамильтон позже написал: «В тот момент в моей голове словно появился гальванический элемент, создавший электрические разряды мыслей. Именно они и привели меня к тем фундаментальным соотношениям между i,j и к, которыми я пользуюсь до сих пор». Он даже высек эти соотношения на мосту Брум-Бридж, и этот замечательный акт математического вандализма был впоследствии увековечен памятной табличкой.
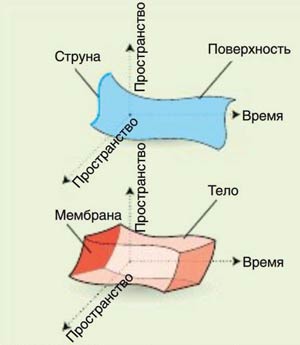
В ТЕОРИИ СТРУН одномерные струны образуют двумерную поверхность при движении во времени. В М-теории двумерные мембраны при движении во времени образуют некоторое тело. Добавляя эти размерности к восьми измерениям системы октонионов, получаем десяти-и одиннадцатимерные пространства
Может показаться странным, что для описания трехмерного пространства необходимо использовать точки из пространства размерности четыре. Три из четырех чисел необходимы для того, чтобы описать повороты в трехмерном пространстве. В целях наглядности можно представить себе самолет, для ориентировки которого необходимо знать углы тангажа (угол между продольной осью самолета и горизонтальной плоскостью), рыскания (отклонения от курса вправо или влево относительно вертикальной оси) и крена (поворот самолета вокруг его продольной оси). Что же касается четвертого числа, то оно необходимо для описания растяжения или сжатия.
Гамильтон потратил остаток жизни, разрабатывая теорию кватернионов и ее приложения. Сегодня многие из его открытий переведены на язык векторной алгебры, теории матриц и т.д. Тем не менее, и кватернионы оказались полезны для решения многих задач, начиная от стабилизации систем в самолетостроении и заканчивая разработкой платформ для компьютерных игр.
После кватернионов
Для определения кватернионов недостаточно просто сказать, что числа i, j и к - это квадратные корни из -1. Неизбежно возникают вопросы, равны ли они между собой, существуют ли они. Эти и подобные вопросы задавал Уильяму Гамильтону его друг, ирландский юрист и математик Джон Грейвс, в беседах с которым и родились основы теории великого ирландского ученого. На следующий день после своего пророческого открытия Гамильтон отправил Грейвсу письмо, в котором описал основные идеи будущей теории. Грейвс ответил девять дней спустя, поздравляя коллегу со смелой идеей, но и добавляя при этом: «Есть что-то, что меня смущает в этой системе. У меня нет уверенности в том, что такое вольное увеличение количества мнимых единиц, а также приписывание им сверхъестественных свойств окажется безнаказанным». А после следовал вопрос: «Если благодаря вашей алхимии появятся три фунта золота, то почему надо на этом останавливаться?» Но, как и Кардано до него, Грейвс отложил свои вопросы и занялся сотворением своего собственного «золота». 26 декабря он вновь написал Гамильтону письмо, в котором описывал новую числовую систему размерности восемь, которую назвал октавы (в наше время она носит название октонионы). Открытие не заинтересовало Гамильтона, но он обещал сделать сообщение о нем в Ирландском королевском обществе, что способствовало бы публикации результатов работы Джона Грейвса. Однако Гамильтон промедлил, и первенство открытия октонионов оказалось за молодым гениальным математиком Артуром Кейли, совершившим его независимо от Грейвса в 1845 г.
ПРОБЛЕМЫ С ПОВОРОТАМИ
Обычно можно перемножать числа в любом порядке. Например, неважно, умножается ли два на три или три на два, - результат будет одним. Тем не менее в системах с большим числом измерений, например в кватернионах и октонионах, порядок сомножителей имеет большое значение. Это можно показать на примере кватернионов, описывающих повороты в пространстве. Возьмем какой-нибудь объект, например книгу, и повернем ее дважды, как показано на верхнем рисунке (сначала вертикально на 180°, чтобы стала видна другая сторона обложки, а затем горизонтально на 90° по часовой стрелке). Если теперь совершить те же самые повороты, но в обратном порядке (рис. внизу), то получится иное положение книги

Почему же Гамильтон так небрежно отнесся к открытию своего друга? Безусловно, он был слишком увлечен собственным открытием, но понимал, что октонионы нарушают некоторые привычные законы арифметики. Он столкнулся с этим даже в открытых им кватернионах. Дело в том, что при перемножении действительных чисел порядок множителей значения не имеет. Иными словами, для действительных чисел операция умножения коммутативна. То же верно и для комплексных чисел. Но для кватернионов это свойство не выполняется. Порядок перемножения двух чисел имеет большое значение, т.к. эта операция с геометрической точки зрения означает поворот в трехмерном пространстве, и изменение порядка умножения может привести к другому повороту. В этом можно убедиться на наглядном примере. Если взять книгу, перевернуть ее так, чтобы стала видна обложка, а затем повернуть по часовой стрелке на четверть оборота так, чтобы стали видны страницы, то получится одно положение книги в пространстве. Если эти же самые операции повторить в обратном порядке, то положение книги будет иным (врезка ПРОБЛЕМЫ С ПОВОРОТАМИ).
Что касается октонионов, то для этих чисел нарушается не только закон коммутативности умножения, но и так называемая ассоциативность этой операции. Иными словами, привычное для действительных чисел тождество (х • у) z = х (у • z) для октонионов не выполняется. Такое нарушение закона ассоциативности кажется привычным для операции вычитания действительных чисел: например, результат операции (3 - 2) - 1 отличен от результата 3 - (2 - 1). Тем не менее к тому, что умножение не обладает этим свойством, необходимо привыкнуть.
В течение почти 100 лет подобные исследования были не более чем математической теорией, упражнением для ума. В наше время неожиданно выяснилось, что «упражнения», оказывается, весьма результативны, например, для современных исследований в физике элементарных частиц и в частности в теории струн.
Симметрия и струны
В 70-80-х гг. XX в. учеными была разработана теория суперсимметрии (впоследствии была доказана связь между суперсимметрией и теорией струн). Выяснилось, что эта теория проявляется на многих фундаментальных уровнях, а во Вселенной существует симметрия между материей и силами природы. Каждая частица материи (например, электрон) имеет своего суперпартнера, который обладает способностью к взаимодействию. И наоборот, каждая частица-переносчик взаимодействия (например, фотон - носитель электромагнитного взаимодействия) обладает своим партнером - частицей материи. Одна из идей, основанная на теории суперсимметрии, заключается в том, что законы физики должны остаться прежними в том случае, если поменять частицы материи и их суперпартнеров местами. Можно представить себе, что наша Вселенная отражается в некотором необычном зеркале, которое не только меняет «право» и «лево» местами, но и заменяет частицы на их суперпартнеров и наоборот. Тем не менее, несмотря на красоту этой теории, физики до сих пор не нашли ее экспериментального подтверждения.
С точки зрения квантовой механики частицы можно рассматривать как волны. Если взять стандартный трехмерный вариант квантовой механики, то в нем существуют специальные объекты, так называемые спиноры, описывающие движение волн частиц материи. С другой стороны, при помощи векторов можно описать движение волн частиц взаимодействия. И те и другие объекты можно описать с помощью различных числовых систем (например, спиноры допускают удобное описание в терминах кватернионов). Следовательно, для определения взаимодействия частиц разного типа необходимо рассматривать эти объекты вместе. Если представить себе систему, в которой существует только пространство и нет времени, и предположить также, что такая система имеет размерность один, два, четыре или восемь, то и частицы материи, и частицы взаимодействия будут волнами, которые можно описать при помощи только одного типа чисел, образующих алгебру вместе с привычными арифметическими операциями. Другими словами, при таких размерностях векторы и спиноры совпадают и описываются с помощью действительных или комплексных чисел, или при помощи кватернионов или октонионов, а их взаимодействия - с помощью простого умножения. В этом случае суперсимметрия обеспечивает универсальное описание частиц материи и их суперпартнеров.
К сожалению, подобная гипотетическая модель, в которой отсутствует время, слишком далека от описания настоящей Вселенной. Но с точки зрения теории струн подобные рассуждения звучат интригующе. Если в каждый конкретный момент времени струна представляет собой одномерный объект, то при движении в пространстве-времени соответственно получается двумерная поверхность. Эта эволюция во времени меняет размерности пространства, в котором действует суперсимметрия, на две единицы - одну из-за размерности струны и одну из-за времени. Таким образом, вместо суперсимметрии в пространстве с размерностями один, два, четыре и восемь мы получаем суперсимметрию в пространствах с размерностью три, четыре, шесть или десять. В течение нескольких десятилетий считалось, что только десятиразмерная модель самосогласованна. Тем не менее, в рамках этой теории существует и так называемая аномалия, из-за которой различные доказательства одного утверждения дают различные результаты. Теория струн «работает» только в пространстве размерности десять. Как мы уже видели, десятимерная теория струн - версия теории, которая использует октонионы. Таким образом, если теория струн верна, то октонионы - не бесполезная выдумка. Более того, октонионы дают повод говорить о причине, по которой наша Вселенная должна иметь размерность десять. При такой размерности частицы материи и частицы-переносчики взаимодействия описываются при помощи одной числовой системы - кватернионов.
Но это еще не все. Недавно физики стали вместо струн рассматривать так называемые мембраны. В каждый момент времени мембрана представляет собой двумерную поверхность, а при движении в пространстве-времени - некоторое тело. Если в теории струн к заветным числам 1, 2, 4 и 8 необходимо было добавлять 2, то теперь, соответственно, 3. Таким образом, работая с мембранами, мы получим суперсимметрию в случае размерностей четыре, пять, семь и 11. И снова удивительным «совпадением» оказывается тот факт, что разработанная физиками М-теория (М от membrane) использует 11 измерений, что позволяет использовать октонионы. К сожалению, М-теория недостаточно разработана, и до сих пор не выписаны базовые уравнения.
Необходимо отметить, что теория струн и М-теория сегодня не имеют экспериментального подтверждения. Они - только прекрасные мечты. Окружающий нас мир не производит впечатления десяти- или одиннадцатимерного, и мы не наблюдаем суперсимметрии между частицами материи и частицами - переносчиками взаимодействия. Дэвид Гросс (David Gross), один из виднейших в мире специалистов по теории струн, говорит лишь о 50% вероятности экспериментального подтверждения теории суперсимметрии на Большом адронном коллайдере.
Из-за такой неопределенности мы все еще далеки от того, чтобы определить, что же такое октонионы: способ описания окружающего нас мира или же просто замечательная математическая головоломка. Безусловно, стройная математическая теория - это само по себе неплохо, но было бы куда лучше, если бы эти странные числа нашли применение в описании фундаментальных законов природы. История комплексных чисел и другие бесчисленные математические открытия, столь активно использующиеся современной физикой, заставляют нас считать, что октонионы ждет блестящее будущее.
Перевод: Д.С. Хованский
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
- An Imaginary Tale: The Story of the Square Root of-1. Paul J. Nahin. Princeton University Press, 1998
- The Octonions. John C. Baez in Bulletin of the American Mathematical Society, Vol. 39, pages 145-205; 2002. Работа и библиография в Интернете: http://math.ucr.edu/home/baez/octonions.
- Ubiquitous Octonions. Helen Joyce in Plus Magazine, Vol. 33: January 2005. http://plus.maths.org/content/33.
- На сайте Scientific American можно найти графическую визуализацию трехмерных поворотов: http://ScientificAmerican.com/may2011/octonions.
ОБ АВТОРАХ

Джон Баэз (John С. Baez) - специалист в области математической физики. В настоящее время работает в Центре квантовых технологий в Сингапуре. Ранее занимался вопросами фундаментальной физики.
Джон Уэрта (John Huerta) защитил диссертацию по математике в Калифорнийском университете в Риверсайде. Работает в области теории суперсимметрии.
Нет комментариев.
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.






