Общая теория относительности Последовательна ли она? Отвечает ли она физической реальности?
Говорят, что прозрение пришло к Альберту Эйнштейну в одно мгновение. Ученый якобы ехал на трамвае по Берну (Швейцария), взглянул на уличные часы и внезапно осознал, что если бы трамвай сейчас разогнался до скорости света, то в его восприятии эти часы остановились бы — и времени бы вокруг не стало. Это и привело его к формулировке одного из центральных постулатов относительности — что различные наблюдатели по-разному воспринимают действительность, включая столь фундаментальные величины, как расстояние и время.
Говоря научным языком, в тот день Эйнштейн осознал, что описание любого физического события или явления зависит от системы отсчета, в которой находится наблюдатель. Если пассажирка трамвая, например, уронит очки, то для нее они упадут вертикально вниз, а для пешехода, стоящего на улице, очки будут падать по параболе, поскольку трамвай движется, в то время как очки падают. У каждого своя система отсчета.
Но хотя описания событий при переходе из одной системы отсчета в другую меняются, есть и универсальные вещи, остающиеся неизменными. Если вместо описания падения очков задаться вопросом о законе природы, вызывающем их падение, то ответ на него будет один и тот же и для наблюдателя в неподвижной системе координат, и для наблюдателя в движущейся системе координат. Закон распределенного движения в равной мере действует и на улице, и в трамвае. Иными словами, в то время как описание событий зависит от наблюдателя, законы природы от него не зависят, то есть, как принято говорить на научном языке, являются инвариантными. В этом и заключается принцип относительности.
Как любую гипотезу, принцип относительности нужно было проверить путем соотнесения его с реальными природными явлениями. Из принципа относительности Эйнштейн вывел две отдельные (хотя и родственные) теории. Специальная, или частная, теория относительности исходит из положения, что законы природы одни и те же для всех систем отсчета, движущихся с постоянной скоростью. Общая теория относительности распространяет этот принцип на любые системы отсчета, включая те, что движутся с ускорением. Специальная теория относительности была опубликована в 1905 году, а более сложная с точки зрения математического аппарата общая теория относительности была завершена Эйнштейном к 1916 году.
Специальная теория относительности
Большинство парадоксальных и противоречащих интуитивным представлениям о мире эффектов, возникающих при движении со скоростью, близкой к скорости света, предсказывается именно специальной теорией относительности. Самый известный из них — эффект замедления хода часов, или эффект замедления времени. Часы, движущиеся относительно наблюдателя, идут для него медленнее, чем точно такие же часы у него в руках.
Время в системе координат, движущейся со скоростями, близкими к скорости света, относительно наблюдателя растягивается, а пространственная протяженность (длина) объектов вдоль оси направления движения — напротив, сжимается. Этот эффект, известный как сокращение Лоренца—Фицджеральда, был описан в 1889 году ирландским физиком Джорджем Фицджеральдом (George Fitzgerald, 1851–1901) и дополнен в 1892 году нидерландцем Хендриком Лоренцем (Hendrick Lorentz, 1853–1928). Сокращение Лоренца—Фицджеральда объясняет, почему опыт Майкельсона—Морли по определению скорости движения Земли в космическом пространстве посредством замеров «эфирного ветра» дал отрицательный результат. Позже Эйнштейн включил эти уравнения в специальную теорию относительности и дополнил их аналогичной формулой преобразования для массы, согласно которой масса тела также увеличивается по мере приближения скорости тела к скорости света. Так, при скорости 260 000 км/с (87% от скорости света) масса объекта с точки зрения наблюдателя, находящегося в покоящейся системе отсчета, удвоится.
Со времени Эйнштейна все эти предсказания, сколь бы противоречащими здравому смыслу они ни казались, находят полное и прямое экспериментальное подтверждение. В одном из самых показательных опытов ученые Мичиганского университета поместили сверхточные атомные часы на борт авиалайнера, совершавшего регулярные трансатлантические рейсы, и после каждого его возвращения в аэропорт приписки сверяли их показания с контрольными часами. Выяснилось, что часы на самолете постепенно отставали от контрольных все больше и больше (если так можно выразиться, когда речь идет о долях секунды). Последние полвека ученые исследуют элементарные частицы на огромных аппаратных комплексах, которые называются ускорителями. В них пучки заряженных субатомных частиц (таких как протоны и электроны) разгоняются до скоростей, близких к скорости света, затем ими обстреливаются различные ядерные мишени. В таких опытах на ускорителях приходится учитывать увеличение массы разгоняемых частиц — иначе результаты эксперимента попросту не будут поддаваться разумной интерпретации. И в этом смысле специальная теория относительности давно перешла из разряда гипотетических теорий в область инструментов прикладной инженерии, где используется наравне с законами механики Ньютона.
Возвращаясь к законам Ньютона, я хотел бы особо отметить, что специальная теория относительности, хотя она внешне и противоречит законам классической ньютоновской механики, на самом деле практически в точности воспроизводит все обычные уравнения законов Ньютона, если ее применить для описания тел, движущихся со скоростью значительно меньше, чем скорость света. То есть, специальная теория относительности не отменяет ньютоновской физики, а расширяет и дополняет ее.
Принцип относительности помогает также понять, почему именно скорость света, а не какая-нибудь другая, играет столь важную роль в этой модели строения мира — этот вопрос задают многие из тех, кто впервые столкнулся с теорией относительности. Скорость света выделяется и играет особую роль универсальной константы, потому что она определена естественнонаучным законом. В силу принципа относительности скорость света в вакууме c одинакова в любой системе отсчета. Это, казалось бы, противоречит здравому смыслу, поскольку получается, что свет от движущегося источника (с какой бы скоростью он ни двигался) и от неподвижного доходит до наблюдателя одновременно. Однако это так.
Благодаря своей особой роли в законах природы скорость света занимает центральное место и в общей теории относительности.
Общая теория относительности
Общая теория относительности применяется уже ко всем системам отсчета (а не только к движущимися с постоянной скоростью друг относительно друга) и выглядит математически гораздо сложнее, чем специальная (чем и объясняется разрыв в одиннадцать лет между их публикацией). Она включает в себя как частный случай специальную теорию относительности (и, следовательно, законы Ньютона). При этом общая теория относительности идёт значительно дальше всех своих предшественниц. В частности, она дает новую интерпретацию гравитации.
Общая теория относительности делает мир четырехмерным: к трем пространственным измерениям добавляется время. Все четыре измерения неразрывны, поэтому речь идет уже не о пространственном расстоянии между двумя объектами, как это имеет место в трехмерном мире, а о пространственно-временных интервалах между событиями, которые объединяют их удаленность друг от друга — как по времени, так и в пространстве. То есть пространство и время рассматриваются как четырехмерный пространственно-временной континуум или, попросту, пространство-время. В этом континууме наблюдатели, движущиеся друг относительно друга, могут расходиться даже во мнении о том, произошли ли два события одновременно — или одно предшествовало другому. К счастью для нашего бедного разума, до нарушения причинно-следственных связей дело не доходит — то есть существования систем координат, в которых два события происходят не одновременно и в разной последовательности, даже общая теория относительности не допускает.

Закон всемирного тяготения Ньютона говорит нам, что между любыми двумя телами во Вселенной существует сила взаимного притяжения. С этой точки зрения Земля вращается вокруг Солнца, поскольку между ними действуют силы взаимного притяжения. Общая теория относительности, однако, заставляет нас взглянуть на это явление иначе. Согласно этой теории, гравитация — это следствие деформации («искривления») упругой ткани пространства-времени под воздействием массы (при этом чем тяжелее тело, например Солнце, тем сильнее пространство-время «прогибается» под ним и тем, соответственно, сильнее его гравитационное поле). Представьте себе туго натянутое полотно (своего рода батут), на которое помещен массивный шар. Полотно деформируется под тяжестью шара, и вокруг него образуется впадина в форме воронки. Согласно общей теории относительности, Земля обращается вокруг Солнца подобно маленькому шарику, пущенному кататься вокруг конуса воронки, образованной в результате «продавливания» пространства-времени тяжелым шаром — Солнцем. А то, что нам кажется силой тяжести, на самом деле является, по сути чисто внешнем проявлением искривления пространства-времени, а вовсе не силой в ньютоновском понимании. На сегодняшний день лучшего объяснения природы гравитации, чем дает нам общая теория относительности, не найдено.
Проверить общую теорию относительности трудно, поскольку в обычных лабораторных условиях ее результаты практически полностью совпадают с тем, что предсказывает закон всемирного тяготения Ньютона. Тем не менее несколько важных экспериментов были произведены, и их результаты позволяют считать теорию подтвержденной. Кроме того, общая теория относительности помогает объяснить явления, которые мы наблюдаем в космосе, — например, незначительные отклонения Меркурия от стационарной орбиты, необъяснимые с точки зрения классической механики Ньютона, или искривление электромагнитного излучения далеких звезд при его прохождении в непосредственной близости от Солнца.
На самом деле результаты, которые предсказывает общая теория относительности, заметно отличаются от результатов, предсказанных законами Ньютона, только при наличии сверхсильных гравитационных полей. Это значит, что для полноценной проверки общей теории относительности нужны либо сверхточные измерения очень массивных объектов, либо черные дыры, к которым никакие наши привычные интуитивные представления неприменимы. Так что разработка новых экспериментальных методов проверки теории относительности остается одной из важнейших задач экспериментальной физики.
ОТО и РТГ: некоторые акценты
1. В бесчисленных книгах – монографиях, учебниках и научно-популярных изданиях, а также в различного типа статьях – читатели привыкли видеть упоминания об общей теории относительности (ОТО) как об одном из величайших достижений нашего века, о замечательной теории, о непременном орудии современной физики и астрономии. Между тем из статьи А. А. Логунова они узнают, что, по его мнению, от ОТО нужно отказаться, что она плоха, непоследовательна и противоречива. Поэтому ОТО требует замены некоторой другой теорией и, конкретно, построенной А. А. Логуновым и его сотрудниками релятивистской теорией гравитации (РТГ).
Возможна ли такая ситуация, когда очень многие ошибаются в оценке ОТО, существующей и изучаемой уже более 70 лет, а лишь несколько человек во главе с А. А. Логуновым действительно выяснили, что ОТО нужно отбросить? Большинство читателей ожидают, вероятно, ответа: такое невозможно. На самом же деле я могу ответить только прямо противоположным образом: и «такое» в принципе возможно, ибо речь идет не о религии, а о науке.
Основатели и пророки различных религий и вероучений создавали и создают свои «священные книги», содержание которых
объявляется истиной в последней инстанции. Если

Перед многими читателями следует, вероятно, извиниться за повторение здесь давно им известного. Но я думаю сейчас и о тех (а опыт показывает, что таких, к сожалению, не так уж мало), чье мнение находит отражение в получаемых нами письмах с различными обвинениями. Эти «критики» полагают, что физики защищают, скажем, теорию относительности и квантовую механику, восхищаются Эйнштейном и Бором в силу невесть чего – философского идеализма, догматизма или невежества, а то и даже в силу групповщины или национализма. Просто стыдно такое читать…
2. Теперь необходимо остановиться на требованиях, предъявляемых к фундаментальным физическим теориям.
Поясним сказанное на примере классической, нерелятивистской механики – механики Ньютона 1 в применении к простейшей в принципе задаче о движении некоторой «точечной» частицы. Как известно, роль такой частицы в задачах небесной механики может играть целая планета или ее спутник. Пусть в момент t0 частица находится в точке A с координатами xiA (t0 ) и имеет скорость viA (t0 ) (здесь i = l, 2, 3, ибо положение точки в пространстве характеризуется тремя координатами, а скорость является вектором). Тогда, если известны все действующие на частицу силы, законы механики позволяют определить положение B и скорость частицы vi в любой последующий момент времени t, то есть найти вполне определенные величины xiB (t) и viB (t). А что было бы, если бы используемые законы механики не давали однозначного ответа и, скажем, в нашем примере предсказывали, что частица в момент t может находиться либо в точке B, либо в совсем другой точке C? Ясно, что такая классическая (неквантовая) теория была бы неполна, или, по упомянутой терминологии, непоследовательна. Ее либо нужно было бы дополнить, сделав однозначной, либо вообще отбросить. Механика Ньютона, как сказано, последовательна – на находящиеся в области ее компетенции и применимости вопросы она дает однозначные и вполне определенные ответы. Удовлетворяет механика Ньютона и второму упомянутому требованию – получаемые на ее основе результаты (и, конкретно, значения координат xi (t) и скорости vi (t)) согласуются с наблюдениями и опытами. Именно поэтому вся небесная механика – описание движения планет и их спутников – до поры до времени целиком базировалась, и с полным успехом, на ньютоновской механике.

3. Но вот в 1859 году Леверье обнаружил, что движение самой близкой к Солнцу планеты – Меркурия несколько отличается от предсказываемого механикой Ньютона. Конкретно оказалось, что, перигелий – ближайшая к Солнцу точка эллиптической орбиты планеты – поворачивается с угловой скоростью на 43 угловых секунды в столетие 2, отличающейся от той, которую следовало бы ожидать при учете всех известных возмущений от других планет и их спутников. Еще ранее Леверье и Адамс столкнулись с аналогичной, по сути дела, ситуацией при анализе движения Урана – наиболее удаленной от Солнца планеты из всех известных в то время. И они нашли объяснение расхождению вычислений с наблюдениями, предположив, что на движение Урана оказывает влияние еще более удаленная планета, названная Нептуном. В 1846 году Нептун действительно был обнаружен на предсказанном месте, и это событие заслуженно считается триумфом ньютоновской механики. Довольно естественно, что Леверье попытался объяснить и упомянутую аномалию в движении Меркурия существованием еще неизвестной планеты – в данном случае некоей планеты Вулкан, движущейся еще ближе к Солнцу. Но во второй раз «фокус не удался» – никакого Вулкана не существует. Тогда начали пытаться изменять ньютоновский закон всемирного тяготения, согласно которому гравитационная сила в применении к системе Солнце – планета изменяется по закону
| F = | mGM☼ | , |
| r 2 |
где
| F ~ | 1 | , |
| r 2 + ε |
где ε – некоторая небольшая величина. Кстати сказать, аналогичный прием используется (правда, без успеха) и в
наши дни для объяснения некоторых неясных вопросов астрономии (речь идет о проблеме скрытой массы; см. например,
цитируемую ниже книгу автора «О физике и астрофизике», с. 148). Но чтобы гипотеза переросла в теорию, нужно
исходить из
|
(1) |
Помимо величин G и М☼, смысл и значения которых указаны выше, здесь a – большая полуось орбиты планеты,
| e = | √ a2 – b2 | – эксцентриситет орбиты (b – ее малая полуось) |
| a |
и
| a3 = | GM☼ | T 2 |
| 4π 2 |
где T – период обращения планеты. Если в формулу (1) подставить лучшие известные сейчас значения
всех величин, а также произвести элементарный пересчет от радианов за оборот к повороту в угловых секундах
(знак ″ ) за столетие, то придем к значению Ψ = 42″.98 / столетие.
Наблюдения сходятся с этим результатом с достигнутой сейчас точностью около ± 0″.1 / столетие
(Эйнштейн в своей первой работе использовал менее точные данные, но в пределах ошибок получил полное согласие теории с
наблюдениями). Формула (1) приведена выше,
В лучшей из мне известных биографий Эйнштейна 3 высказывается и обосновывается мнение, что объяснение поворота перигелия Меркурия явилось «самым сильным эмоциональным событием за всю научную жизнь Эйнштейна, а быть может, и за всю его жизнь». Да, это был «звездный час» Эйнштейна. Но именно для него самого. По ряду причин (достаточно упомянуть о войне) для самой ОТО для выхода на мировую арену как этой теории, так и ее создателя «звездным часом» стало другое событие, происшедшее 4 года спустя – в 1919 г. Дело в том, что в той же работе, в которой была получена формула (1), Эйнштейн сделал важное предсказание: лучи света, проходящие вблизи Солнца, обязаны искривляться, причем их отклонение должно составлять
|
(2) |
где r – ближайшее расстояние между лучом и центром Солнца, а r☼ = 6.96·1010 см – радиус Солнца (точнее, радиус солнечной фотосферы); таким образом, максимальное отклонение, которое можно наблюдать, составляет 1.75 угловых секунды. Как ни мал такой угол (примерно под таким углом взрослый человек виден с расстояния в 200 км), он мог быть измерен уже в то время оптическим методом путем фотографирования звезд на небе в окрестности Солнца 4. Именно такие наблюдения были произведены двумя английскими экспедициями во время полного солнечного затмения 29 мая 1919 года. Эффект отклонения лучей в поле Солнца был при этом установлен со всей определенностью и находится в согласии с формулой (2), хотя точность измерений в связи с малостью эффекта была невелика. Однако отклонение вдвое меньшее, чем согласно (2), т. е. на 0″.87, было исключено. Последнее весьма важно, ибо отклонение на 0″.87 (при r = r☼) можно получить уже из ньютоновской теории (сама возможность отклонения света в поле тяжести была отмечена еще Ньютоном, а выражение для угла отклонения, вдвое меньшее, чем согласно формуле (2), было получено в 1801 году; другое дело, что это предсказание было забыто и Эйнштейн о нём не знал). 6 ноября 1919 года результаты экспедиций были доложены в Лондоне на совместном заседании Королевского общества и Королевского астрономического общества. Какое они произвели впечатление, ясно из того, что сказал на этом заседании председательствовавший Дж. Дж. Томсон: «Это самый важный результат, полученный в связи с теорией гравитации со времен Ньютона… Он представляет собой одно из величайших достижений человеческой мысли».
Эффекты ОТО в Солнечной системе, как мы видели, весьма малы. Объясняется это тем, что гравитационное поле Солнца (не говоря уже о планетах) является слабым. Последнее означает, что ньютоновский гравитационный потенциал Солнца
| φ☼ = – | GM☼ |
| r |
по абсолютной величине мал по сравнению с квадратом скорости света c 2. Так, даже при r = r☼ (то есть на фотосфере Солнца)
| |φ☼| / c2 = | GM☼ | = 2,12 ·10 – 6. |
| c2 r☼ |
Напомним теперь результат, известный из школьного курса физики: для круговых орбит планет
|φ☼| = v2, где v – скорость планеты. Поэтому слабость
гравитационного поля можно характеризовать более наглядным параметром
v 2/c 2, который для Солнечной системы, как мы
видели, не превосходит значения
| (φ☼ / c 2 ) = | v 4 | ≤ 4 ·10 – 12. |
| c 4 |
Об измерениях с нужной точностью, скажем, отклонения лучей в пределах Солнечной системы можно пока только мечтать.
Впрочем, проекты соответствующих экспериментов уже обсуждаются. В связи со сказанным физики и говорят, что ОТО
проверена в основном лишь для слабого гравитационного поля. Но мы (я, во всяком случае)
4. В свете всего изложенного критика ОТО А. А. Логуновым представляется особенно удивительной. Но в согласии со сказанным в начале настоящей статьи отметать эту критику без анализа нельзя. Еще в большей степени нельзя без детального анализа высказать суждение о предлагаемой А. А. Логуновым РТГ – релятивистской теории гравитации.
К сожалению, на страницах научно-популярных изданий проводить такой анализ совершенно невозможно. В своей
статье А. А. Логунов, по сути дела, лишь декларирует и комментирует свою позицию. Никак иначе не могу
поступить
Так вот, мы считаем, что ОТО является последовательной физической теорией – на все правильно и четко поставленные вопросы, допустимые в области ее применимости, ОТО дает однозначный ответ (последнее относится, в частности, к времени запаздывания сигналов при локации планет). Не страдает ОТО и какими-либо дефектами математического или логического характера 5. Нужно, правда, пояснить, что выше имеется в виду при употреблении местоимения «мы». «Мы» – это, конечно, и я сам, но также и все те советские и иностранные физики, с которыми мне приходилось обсуждать ОТО, а в ряде случаев и ее критику А. А. Логуновым. Великий Галилей еще четыре столетия тому назад говорил: в вопросах науки мнение одного бывает дороже мнения тысячи. Другими словами, большинством голосов научные споры не решаются. Но, с другой стороны, совершенно очевидно, что мнение многих физиков, вообще говоря, значительно убедительнее, или, лучше сказать, надежнее и весомее, мнения одного физика. Поэтому переход от «я» к «мы» имеет здесь важное значение.
Полезно и уместно будет, надеюсь, сделать еще несколько замечаний.
Почему А. А. Логунову так не нравится ОТО? Главная причина состоит в том, что в ОТО, вообще говоря, нет понятия об энергии и импульсе в привычной нам из электродинамики форме и, говоря его словами, имеет место отказ «от представления гравитационного поля как классического поля типа Фарадея-Максвелла, обладающего хорошо определенной плотностью энергии-импульса». Да, последнее в некотором смысле верно, но объясняется тем, что «в римановой геометрии в общем случае нет нужной симметрии относительно сдвигов и поворотов, то есть нет… группы движения пространства-времени». Геометрия же пространства-времени согласно ОТО – это риманова геометрия. Именно поэтому, в частности, лучи света отклоняются от прямой линии, проходя вблизи Солнца.
Одним из крупнейших достижений математики прошлого века стало создание и развитие Лобачевским, Бойяи, Гауссом, Риманом
и их последователями неевклидовой геометрии. Тогда же возник вопрос: какова на самом деле геометрия физического
пространства-времени, в которой мы живем? Как сказано, согласно ОТО эта геометрия неевклидова, риманова, а не
псевдоевклидова геометрия Минковского (об этой геометрии подробнее рассказано в статье А. А. Логунова). Эта
геометрия Минковского явилась, можно сказать, порождением специальной теории относительности (СТО) и пришла на смену
абсолютному времени и абсолютному пространству Ньютона. Последнее непосредственно до создания СТО в 1905 году
пытались отождествить с неподвижным эфиром Лоренца. Но от лоренцова эфира, как от абсолютно неподвижной механической
среды,
5. Если говорить о различии между электромагнитным полем и, следовательно, электродинамикой и гравитационным полем (ОТО представляет собой как раз теорию такого поля), то необходимо отметить следующее. Выбором системы отсчета уничтожить (обратить в нуль) даже локально (в малой области) все электромагнитное поле невозможно. Поэтому если плотность энергии электромагнитного поля
| W = | E 2 + H 2 |
| 8π |
(E и H – напряженности соответственно электрического и магнитного полей) отлична от нуля в какой-нибудь системе отсчета, то она будет отлична от нуля и в любой другой системе отсчета. Гравитационное же поле, грубо говоря, значительно сильнее зависит от выбора системы отсчета. Так, однородное и постоянное гравитационное поле (то есть поле тяжести, вызывающее ускорение g помещенных в него частиц, не зависящее от координат и времени) можно полностью «уничтожить» (обратить в нуль) переходом к равномерно-ускоренной системе отсчета. Это обстоятельство, составляющее основное физическое содержание «принципа эквивалентности», было впервые отмечено Эйнштейном в статье, опубликованной в 1907 году и явившейся первой на пути создания ОТО 6.
Если гравитационное поле отсутствует (в частности, вызываемое им ускорение g равно нулю), то равна нулю и плотность отвечающей ему энергии. Отсюда ясно, что в вопросе о плотности энергии (и импульса) теория гравитационного поля должна радикально отличаться от теории электромагнитного поля. Такое утверждение не изменяется в связи с тем фактом, что в общем случае гравитационное поле не может быть «уничтожено» выбором системы отсчета.
Эйнштейн понимал это еще до 1915 года, когда завершил создание ОТО. Так, в 1911 году он писал: «Конечно, нельзя любое поле тяжести заменить состоянием движения системы без гравитационного поля, точно так же как нельзя преобразовать все точки произвольно движущейся среды к покою посредством релятивистского преобразования». А вот выдержка из статьи 1914 года: «Предварительно сделаем еще одно замечание для устранения напрашивающегося недоразумения. Сторонник обычной современной теории относительности (речь идет о СТО – В. Л. Г.) с известным правом называет «кажущейся» скорость материальной точки. Именно, он может выбрать систему отсчета так, что материальная точка имеет в рассматриваемый момент скорость, равную нулю. Если же существует система материальных точек, которые обладают разными скоростями, то он уже не может ввести такую систему отсчета, чтобы скорости всех материальных точек относительно этой системы обращались в нуль. Аналогичным образом физик, стоящий на нашей точке зрения, может называть «кажущимся» гравитационное поле, поскольку соответствующим выбором ускорения системы отсчета он может достичь того, чтобы в определенной точке пространства-времени гравитационное поле обращалось в нуль. Однако примечательно, что обращение в нуль гравитационного поля посредством преобразования в общем случае не может быть достигнуто для протяженных гравитационных полей. Например, гравитационное поле Земли нельзя сделать равным нулю посредством выбора подходящей системы отсчета». Наконец, уже в 1916 г., отвечая на критику ОТО, Эйнштейн еще раз подчеркивал то же самое: «Никоим образом нельзя также утверждать, что поле тяжести в какой-либо мере объясняется чисто кинематически: "кинематическое, нединамическое понимание гравитации" невозможно. Мы не можем получить любое гравитационное поле посредством простого ускорения одной галилеевой системы координат относительно другой, поскольку таким путем возможно получить поля только определенной структуры, которые, однако, должны подчиняться тем же законам, что и все другие гравитационные поля. Это еще одна формулировка принципа эквивалентности (специально для применения этого принципа к гравитации)».
Невозможность «кинематического понимания» гравитации в сочетании с принципом эквивалентности и обусловливают переход в ОТО от псевдоевклидовой геометрии Минковского к римановой геометрии (в этой геометрии пространство-время обладает, вообще говоря, отличной от нуля кривизной; наличие такой кривизны и отличает «истинное» гравитационное поле от «кинематического»). Физические особенности гравитационного поля обусловливают, повторим это, и радикальное изменение роли энергии и импульса в ОТО по сравнению с электродинамикой. При этом как использование римановой геометрии, так и невозможность применять привычные из электродинамики энергетические представления не препятствуют, как уже подчеркивалось выше, тому, что из ОТО следуют и могут быть вычислены вполне однозначные значений для всех наблюдаемых величин (угла отклонения световых лучей, изменения элементов орбит у планет и двойных пульсаров и т. д. и т. п.).
Нелишним будет, наверное, отметить и то обстоятельство, что ОТО можно сформулировать и в привычном из электродинамики виде с использованием понятия о плотности энергии-импульса (об этом см. цитированную статью Я. Б. Зельдовича и Л. П. Грищука 7. Однако вводимое при этом пространство Минковского является чисто фиктивным (ненаблюдаемым), и речь идет лишь о той же ОТО, записанной в нестандартной форме. Между тем, повторим это, А. А. Логунов считает используемое им в релятивистской теории гравитации (РТГ) пространство Минковского реальным физическим, а значит, наблюдаемым пространством.
6. В этом плане особенно важен второй из вопросов, фигурирующих в заголовке настоящей статьи: отвечает ли ОТО физической реальности? Другими словами, что говорит опыт – верховный судья при решении судьбы любой физической теории? Этой проблеме – экспериментальной проверке ОТО посвящены многочисленные статьи и книги 8. Вывод при этом вполне определенен – все имеющиеся данные экспериментов или наблюдений либо подтверждают ОТО, либо не противоречат ей. Однако, как мы уже указывали, проверка ОТО производилась и происходит в основном лишь в слабом гравитационном поле. Кроме того, любой эксперимент имеет ограниченную точность. В сильных гравитационных полях (грубо говоря, в случае, когда отношение |φ| / c 2 не мало; см. выше) ОТО еще в достаточно полной мере не проверена. Для этой цели можно сейчас практически использовать лишь астрономические методы, касающиеся очень далекого космоса: изучения нейтронных звезд, двойных пульсаров, «черных дыр», расширения и строения Вселенной, как говорят, «в большом» – на огромных просторах, измеряемых миллионами и миллиардами световых лет. Многое в этом направлении уже сделано и делается. Достаточно упомянуть об исследованиях двойного пульсара PSR 1913+16, для которого (как и вообще для нейтронных звезд) параметр |φ| / c 2 уже порядка 0,1. Кроме того, в этом случае удалось выявить эффект порядка (v / c) 5, связанный с излучением гравитационных волн. В грядущих десятилетиях открывается еще больше возможностей для исследования процессов в сильных гравитационных полях.
Путеводной звездой в этих захватывающих дух исследованиях является в первую очередь ОТО. Вместе с тем,
естественно, обсуждаются и некоторые другие возможности – иные, как иногда говорят, альтернативные, теории
гравитации. Например, в ОТО, как и в теории всемирного тяготения Ньютона, гравитационная постоянная G
действительно считается постоянной величиной. Одной из самых известных теорий гравитации, обобщающих (или, точнее,
расширяющих) ОТО, является теория, в которой гравитационная «постоянная» считается уже новой скалярной функцией –
величиной, зависящей от координат и времени. Наблюдения и измерения свидетельствуют, однако, о том, что возможные
относительные изменения G со временем очень малы – составляют,
7. А. А. Логунов, отправляясь от критики ОТО, уже более 10 лет строит некоторую альтернативную – отличную от ОТО теорию гравитации. При этом многое изменялось в ходе работы, а принятый сейчас вариант теории (это и есть РТГ) особенно подробно изложен в статье, занимающей около 150 страниц и содержащей около 700 только пронумерованных формул 9. Очевидно, что детальный разбор РТГ возможен лишь на страницах научных журналов. Только после такого разбора можно будет сказать, последовательна ли РТГ, не содержит ли она математических противоречий и т. д. Насколько я мог понять, РТГ отличается от ОТО отбором лишь части решений ОТО – все решения дифференциальных уравнений РТГ удовлетворяют уравнениям ОТО, но, как утверждают авторы РТГ, не наоборот. При этом делается заключение о том, что в отношении глобальных вопросов (решений для всего пространства-времени или его больших областей, топологии и т. п.) отличия между РТГ и ОТО, вообще говоря, радикальны. Что же касается всех экспериментов и наблюдений, произведенных в пределах Солнечной системы, то, насколько я понимаю, РТГ не может вступить в противоречие с ОТО. Если это так 10, то предпочесть РТГ (по сравнению с ОТО) на основе известных опытов в Солнечной системе невозможно. Что же касается «черных дыр» и Вселенной, то авторы РТГ утверждают, что их выводы существенно отличны от выводов ОТО, но какие-либо конкретные данные наблюдений, свидетельствующие в пользу РТГ, нам неизвестны. В такой ситуации РТГ А. А. Логунова (если РТГ действительно отличается от ОТО по существу, а не только способом изложения и выбором одного из возможных классов координатных условий; см. статью Я. Б. Зельдовича и Л. П. Грищука 11) может рассматриваться лишь как одна из допустимых, в принципе, альтернативных теорий гравитации.
Некоторых читателей могут насторожить оговорки типа: «если это так», «если РТГ действительно отличается от ОТО». Не стремлюсь ли я таким образом застраховаться от ошибок? Нет, я не боюсь ошибиться уже в силу убеждения в том, что существует лишь одна гарантия безошибочности – вообще не работать, а в данном случае не обсуждать научные вопросы. Другое дело, что уважение к науке, знакомство с ее характером и историей побуждают к осторожности. Категоричность же высказываний далеко не всегда свидетельствует о наличии подлинной ясности и, в общем, не способствует установлению истины. РТГ А. А. Логунова в ее современной форме сформулирована совсем недавно и подробно еще не обсуждена в научной литературе. Поэтому, естественно, и я не имею о ней окончательного мнения. К тому же в научно-популярном журнале ряд возникающих вопросов обсуждать невозможно, да и неуместно. Вместе с тем, конечно, в связи с большим интересом читателей к теории гравитации освещение на доступном уровне этого круга вопросов, в том числе и дискуссионных, на страницах «Науки и жизни» представляется оправданным.
Итак, руководствуясь мудрым «принципом наибольшего благоприятствования», в настоящее время следует считать РТГ альтернативной теорией гравитации, нуждающейся в соответствующем анализе и обсуждении. Тем, кому эта теория (РТГ) нравится, кого она интересует, никто не мешает (и, конечно, не должен мешать) ее развивать, предлагать возможные пути экспериментальной проверки.
Вместе с тем говорить о том, что ОТО в настоящее время в
* Действительно, как указано в выходных данных, тираж журнала «Наука и жизнь» № 4, 1987 г. был равен 3 млн. 475 тыс. экземпляров. В последние годы тираж составлял всего несколько десятков тысяч экземпляров, превысив 40 тыс. лишь в 2002 г. (прим. – А. М. Крайнев).
1 Кстати сказать, в 1987 году исполняется 300 лет со дня первой
публикации великой книги Ньютона «Математические начала натуральной философии». Ознакомление с историей создания этого
труда, не говоря уже о нем самом, очень поучительно. Впрочем, то же относится ко всей деятельности Ньютона, с которой
неспециалистам у нас не
2 Приводится величина поворота по современным измерениям (у Леверье фигурировал поворот на 38 секунд). Напомним для наглядности, что Солнце и Луна видны с Земли под углом около 0.5 углового градуса – 1800 угловых секунд.
3 A. Pals «Subtle is the Lord…» The Science and Life of Albert Einstein. Oxford Univ. Press, 1982. Целесообразно было бы издать русский перевод этой книги.
4 Последнее возможно во время полных солнечных затмений; фотографируя ту же часть неба, скажем, через полгода, когда Солнце переместилось на небесной сфере, получаем для сравнения картину, не искаженную в результате отклонения лучей под влиянием гравитационного поля Солнца.
5 За подробностями я должен отослать к статье Я. Б. Зельдовича и Л. П. Грищука, недавно опубликованной в «Успехах физических наук» (т. 149, с. 695, 1986 г.), а также к цитированной там литературе, в частности к статье Л. Д. Фаддеева («Успехи физических наук», т. 136, с. 435, 1982 г.).
6 Выдержки из этой статья, а также ссылки на источники нижеследующих цитат можно найти в книге В. Л. Гинзбурга «О теории относительности», М., Наука, 1979.
7 См. сноску 5.
8 См. К. Уилл. «Теория и эксперимент в гравитационной физике». М., Энергоиэдат, 1985; см. также В. Л. Гинзбург. О физике и астрофизике. М., Наука, 1985, и указанную там литературу.
9 А. А. Логунов и М. А. Мествиришвили. «Основы релятивистской теории гравитации». Журнал «Физика элементарных частиц и атомного ядра», т. 17, выпуск 1, 1986 г.
10 В работах А. А. Логунова имеются иные утверждения и конкретно считается, что для времени запаздывания сигнала при локации, скажем, Меркурия с Земли, из РТГ получается значение, отличное от следующего из ОТО. Точнее, утверждается, что ОТО вообще не дает однозначного предсказания времени запаздывания сигналов, то есть ОТО непоследовательна (см. выше). Однако такой вывод является, как нам представляется, плодом недоразумения (это указано, например, в цитированной статье Я. Б. Зельдовича и Л. П. Грищука, см. сноску 5): разные результаты в ОТО при использовании разных систем координат получаются лишь потому, что сравниваются лоцируемые планеты, находящиеся на различных орбитах, а потому и обладающие разными периодами обращения вокруг Солнца. Наблюдаемые с Земли времена запаздывания сигналов при локации определенной планеты, согласно ОТО и РТГ, совпадают.
11 См. сноску 5.
Подробности для любознательных
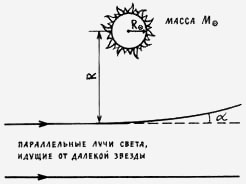 |
Отклонение света и радиоволн в гравитационном поле Солнца. Обычно в качестве идеализированной модели Солнца берут
статический сферически-симметричный шар радиуса R☼ ~ 6.96·10 10 см, масса Солнца М☼ ~ 1.99·10 30 кг (в 332958 раз больше массы Земли). Отклонение света максимально для
лучей, которые едва касаются Солнца, то есть при R ~ R☼, и равно:
φ ≈ 1″.75 (угловых секунд). Этот угол весьма мал – примерно под таким углом виден
взрослый человек с расстояния в 200 км, и поэтому точность измерения гравитационного искривления лучей до
недавнего времени была невысокой. Последние оптические измерения, выполненные во время солнечного затмения
30 июня 1973 года, имели погрешность приблизительно 10 %. Сегодня благодаря появлению
радиоинтерферометров «со сверхдлинной базой» (больше 1000 км) точность измерения углов резко повысилась.
Радиоинтерферометры позволяют надежно измерять угловые расстояния и изменения углов величиной порядка
На рисунке показано отклонение только одного из лучей, приходящих от далекого источника. В действительности искривлены оба луча.
ГРАВИТАЦИОННЫЙ ПОТЕНЦИАЛ
В 1687 году появился фундаментальный труд Ньютона «Математические начала натуральной философии» (см. «Наука и жизнь» № 1, 1987 г.), в котором был сформулирован закон всемирного тяготения. Этот закон гласит, что сила притяжения между двумя любыми материальными частицами прямо пропорциональна их массам M и m и обратно пропорциональна квадрату расстояния r между ними:
| F = G | Mm | . |
| r 2 |
Коэффициент пропорциональности G стал называться гравитационной постоянной, он необходим для согласования размерностей в правой и левой частях ньютоновой формулы. Еще сам Ньютон с весьма высокой для своего времени точностью показал, что G – величина постоянная и, следовательно, открытый им закон тяготения универсален.
Две притягивающиеся точечные массы M и m фигурируют в формуле Ньютона равноправно. Другими словами, можно считать, что они обе служат источниками гравитационного поля. Однако в конкретных задачах, в частности в небесной механике, одна из двух масс часто бывает очень мала по сравнению с другой. Например, масса Земли MЗ ≈ 6 ·10 24 кг намного меньше массы Солнца M☼ ≈ 2 ·10 30 кг или, скажем, масса спутника m ≈ 10 3 кг не идет ни в какое сравнение с земной массой и поэтому практически никак не влияет на движение Земли. Такую массу, которая сама не возмущает гравитационного поля, а служит как бы зондом, на который это поле действует, называют пробной. (Точно так же в электродинамике существует понятие «пробного заряда», то есть такого, который помогает обнаружить электромагнитное поле.) Поскольку пробная масса (или пробный заряд) вносит в поле пренебрежимо малый вклад, для такой массы поле становится «внешним» и его можно характеризовать величиной, называемой напряженностью. По существу, ускорение свободного падения g – это напряженность поля земного тяготения. Второй закон ньютоновой механики дает тогда уравнения движения точечной пробной массы m. Например, именно так решаются задачи баллистики и небесной механики. Заметим, что для большинства таких задач теория тяготения Ньютона и сегодня обладает вполне достаточной точностью.
Напряженность, как и сила, – величина векторная, то есть в трехмерном пространстве она определяется тремя числами – компонентами вдоль взаимно перпендикулярных декартовых осей х, у, z. При смене системы координат – а такие операции нередки в физических и астрономических задачах – декартовы координаты вектора преобразуются некоторым хоть и не сложным, но зачастую громоздким образом. Поэтому вместо векторной напряженности поля удобно было бы использовать соответствующую ей скалярную величину, из которой силовая характеристика поля – напряженность – получалась бы с помощью какого-нибудь простого рецепта. И такая скалярная величина существует – она называется потенциалом, а переход к напряженности осуществляется простым дифференцированием. Отсюда следует, что ньютоновский гравитационный потенциал, создаваемый массой M, равен
| φ = | GM | . |
| r |
Представим себе теперь пробную массу m, которая равномерно вращается по круговой орбите вокруг источника поля M. Согласно второму закону Ньютона, ее движение под действием сил тяготения описывается уравнением
| mv 2 | = G | Mm | , |
| r | r 2 |
откуда и следует равенство |φ| = v 2.
В математике теория тяготения Ньютона иногда называется «теорией потенциала». В свое время теория ньютонова потенциала послужила образцом для теории электричества, а затем представления о физическом поле, сформировавшиеся в электродинамике Максвелла, в свою очередь, стимулировали появление общей теории относительности Эйнштейна. Переход от релятивистской теории тяготения Эйнштейна к частному случаю ньютоновой теории гравитации как раз и соответствует области малых значений безразмерного параметра |φ| / c 2.
Академик В. Гинзбург
Комментарии (3):
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.







Спасибо автору статьи!!!
Много интересных и правильных мыслей.
Однако считаю, что некоторые мифы, связанные с популялизированием гравэффектов по А.Эйншейну, надо неск. "подточить".
Цитата статьи:
>Представьте себе туго натянутое полотно (своего рода батут)... и далее по тексту.
Описан мысленный эксперимент, который призван объяснить_устаканить в понимании читателей связь гравитации и искривления пространства_времени.
Вновь цитата статьи:
>Согласно общей теории относительности, Земля обращается вокруг Солнца подобно маленькому шарику, пущенному кататься вокруг конуса воронки...
но "кататься вокруг конуса воронки" есть сам по себе процесс во времени (ключевое слово кататься)!!!, а время то мы уже "вложили" в топологический образ конуса воронки и теперь используем уже неск. другое время, отличное от того, что уже "зашито" в этом самом конусе.
Т.е. подразумевается одновременное (хоть и тавтология, но...) использование двух не "перекрывающихся" по своей сути понятий о времени.