Квантовая механика убила старый миф, заключающийся в том, что вакуум есть пустое пространство. Теперь все согласны, что вакуум заполнен нулевыми флуктуациями релятивистских квантовых полей. Однако новая точка зрения создала новые мифы. Главный миф – проблема космологической константы или «невообразимая легкость пространства времени».

Частичный перевод замечательной статьи Г.Е. Воловика, Vacuum Energy: Myths and Reality;

1. Введение: старые и новые мифы

Он базируется на предположении, что естественное значение плотности энергии квантового вакуума (и, следовательно, космологической константы) определяется планковским масштабом энергии

\[{{\Lambda }_{natural}}\sim \frac{E_{Planck}^{4}}{{{\hbar }^{2}}{{c}^{3}}}\] (1)

Это значение фантастически велико по сравнению с наблюдаемым верхним пределом КК. Это заставляет нас думать, что Вселенная драматически не естественна.

Родственный миф – нулевая энергия бозонного квантованного поля и отрицательная энергия дираковского моря фермионных квантованных полей – доминирующие источники вакуумной энергии. Суммирование по всем модам вплоть до масштаба планковской энергии дает оценку, соответствующую (1). Возможно,  суперсимметрия между фермионами и бозонами может уменьшить обрезание, но результат все еще будет невообразимо высоким.

Но зададимся вопросом: действительно ли уравнение (1) представляет естественное значение вакуумной энергии?

Один из мифов состоит в том, что величина вакуумной энергии важна только в присутствие гравитации, а в остальных случаях она может быть устранена сдвигом энергии. Это не так. Рассмотрение многочастичной системы, выполненное в Разделе 3, демонстрирует, что соответствующим образом введенная плотность вакуумной энергии хорошо определена в любой системе (релятивистской или нерелятивистской, с гравитацией или без) и не зависит от выбора нуля. Макроскопические свойства квантового вакуума не зависят от того, имеется ли гравитация в системе или нет. Если так, то проблемы, связанные с вакуумной энергией могут быть рассмотрены в более общем контексте, без ссылок на системы с гравитацией.

Конечно, существуют  многочастичные  системы, где динамические метрические поля появляются как коллективные моды квантового вакуума. Кроме того мы имеем примеры, в которых гравитация появляется вместе с ингредиентами Стандартной модели – киральными фермионами и калибровочными полями. Однако эти примеры не существенны при обсуждении общих свойств квантового вакуума, связанных с вакуумной энергией.

Следующий миф – энергия фальшивого вакуума. Фальшивый вакуум – состояние, соответствующее локальному минимуму энергии. Он имеет более высокую энергию, чем истинный вакуум, соответствующий абсолютному минимуму. По этой причине предполагается, что если $\Lambda =0$ в истинном вакууме, она должна быть положительной (и большой?) в фальшивом вакууме. Это важно для такого явления как инфляция – экспоненциального расширения Вселенной. Близкий по смыслу миф – влияние нарушения симметрии фазового перехода на вакуумную энергию.

Еще один миф – зависимость энергии вакуума от его содержания. Действительно, на первый взгляд это утверждение кажется правильным. Вакуум сложная структура, содержащая много вкладов от различных квантовых полей. В частности имеется много фермионных компонент, каждая со своей собственной массой. Поэтому вакуумная энергия должна зависеть от фермионных масс, хиггсовских полей и т.д.

Как следует из опыта работы с конденсированной материей, краткий ответ на поставленный выше вопрос звучит так: естественное значение вакуумной энергии равно нулю, и, следовательно, не зависит от содержания вакуума, от расходимости энергии нулевых колебаний, от того, является ли вакуум фальшивым или истинным, от фазовых переходов в вакууме и т.д.

Если естественное значение вакуумной энергии равно нулю, то должны ли мы вернуться к старому мифу о том, что вакуум не гравитирует?  Нет, не должны, так как наблюдения ненулевой КК привели к новому мифу о том, что наблюдение вызвало кризис в физике. Легче предположить, что вакуумная энергия равна нулю, чем искать недостающие 120 порядков.

Одно из возмущений вакуума, приводящее к ненулевой вакуумной энергии, это граничные условия. Это возмущение приводит к эффекту Казимира. Можно показать что,  нулевая энергия между пластинами в эффекте Казимира должна гравитировать, в то время как в вакууме вне пластин не должна. Сходный вопрос был поставлен Полчинским: почему энергия нулевых колебаний должна гравитировать в среде, окружающей атом (лембовский сдвиг), но не в вакууме.

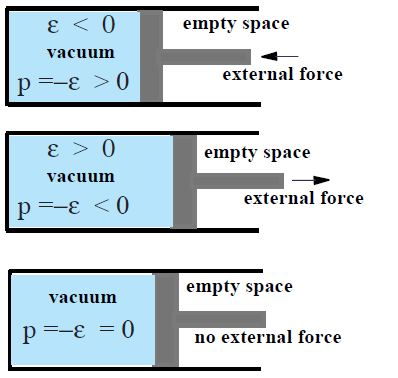
Рис.1. Если вакуумная энергия отрицательна $\left( \varepsilon <0 \right),$ вакуум пытается расшириться $\left( p=-\varepsilon >0 \right),$ двигая поршень вправо. Чтобы достичь равновесия, необходимо приложить внешнюю силу, которая будет толкать поршень влево и компенсировать положительное давление вакуума $\left( {{p}_{vac}}=-{{\varepsilon }_{vac}} \right).$ Точно такая ситуация имеет место в конденсированной материи (газе, жидкости и твердом теле) при $T=0.$ Аналогично рассуждая, мы видим, что если вакуумная энергия положительна, то  приложенная сила должна тянуть поршень вправо, чтобы скомпенсировать отрицательное давление вакуума. Аналогичная ситуация имеет место в жидкости и твердом теле при $T=0,$ но не в газе, который может находиться в равновесии только при положительном давлении. В отличие от газа, жидкость и твердое тело самосогласованные субстанции в том смысле, что могут находиться в равновесии без внешних сил. Поэтому в отсутствие взаимодействия с окружающей средой, плотность энергии вакуума и вакуумное давление приобретают свое естественное значение ${{\varepsilon }_{vac}}=-{{p}_{vac}}=0$.

2. Каково естественное значение вакуумной энергии?

Давайте начнем с проблемы космологической константы, которая базируется на мифе, что естественное значение плотности энергии квантового вакуума и, следовательно, космологической константы определяется планковским масштабом энергии.

2.1. Естественное микроскопическое значение

Чтобы проникнуть в суть проблемы, давайте посмотрим, является ли это предположение правильным для таких квантовых многочастичных систем как квантовая жидкость или твердое тело. На первый взгляд, оно кажется правильным. Микроскопическая (атомная физика) определяет характерный масштаб величин, описывающих жидкость или твердое тело. Роль планковской длины играет межатомное расстояние. Роль планковской энергии играет либо температура Дебая, либо температура плавления, либо температура перехода в сверхтекучее состояние. В результате мы имеем следующие оценки для характерной температуры, плотности энергии и давления

\[{{T}_{micro}}\sim {{E}_{Planck}}\sim \hbar c/a;\quad {{\varepsilon }_{micro}}\sim {{p}_{micro}}\sim \frac{E_{Planck}^{4}}{{{\hbar }^{3}}{{c}^{3}}}\] (2)

Здесь $c$- скорость звука или других бозонных или фермионных возбуждений, играющих роль максимально достижимой скорости (скорости света).

2.2 Естественное макроскопическое значение

Несмотря на внешнюю схожесть формул (1) и (2), предположение о том, что микроскопический (планковский) масштаб естественно входит в вакуумную энергию неправильно. 

\[{{T}_{macro}}=0;\quad {{p}_{macro}}=0\] (3)

Эти соотношения демонстрируют гигантскую разницу между параметрами микро и макрофизики. Многочастичная система как целое подчиняется законам макрофизики, которые не зависят от деталей микрофизики. Поэтому общие свойства любой системы будут странными, если вакуум не подчиняется тем же правилам. Давление вакуума – макрофизическая характеристика, поэтому естественное значение плотности вакуумной энергии должно быть равно нулю

\[{{\Lambda }_{natural}}={{\varepsilon }_{vac}}=-{{p}_{vac}}=0\] (4)

(при условии, что мы считаем, что наша Вселенная не взаимодействует с «окружающей средой»).

3. Абсолютное значение энергии вакуума имеет значение только для гравитации

Можно привести доводы в пользу того, что вакуумная энергия важна только для гравитации, т.е. только гравитация чувствительна к вакуумной энергии, во всех остальных случаях вакуумная энергия может быть устранена сдвигом нулевого уровня. Вот почему аналогия с конденсированной материей не имеет смысла. Пока гравитация не возникает в конденсированной материи. Это еще один миф.

Во-первых, мы интересуемся не абсолютным значением полной энергии вакуума. Нас интересует космологическая константа, которая представляет плотность энергии вакуума, а эта плотность связана с давлением вакуума уравнением состояния

\[{{\varepsilon }_{vac}}=-{{p}_{vac}}\] (5)

Независимо от того, присутствует или отсутствует гравитация, вакуум есть субстанция с таким уравнением состояния. И это не зависит от выбора нулевого уровня энергии. Давайте рассмотрим, как уравнение состояния (5) появляется в вакууме (основном состоянии) конденсированной материи.

3.1. Квантовая полевая теория конденсированной материи.

Правила игры очень просты: основное состояние конденсированной материи –аналог вакуума. Частицеподобные возбуждения выше основного состояния –квазичастицы. Они служат аналогом материи. Квазичастицы не рассеиваются на исходных атомах жидкости или твердого тела, если жидкость или твердое тело находится в основном состоянии (но ведь тогда и нет квазичастиц?). Именно по этой причине для квазичастиц однородное основное состояние является идеальным вакуумом.

Первое, что мы должны установить это то, что термодинамический потенциал в квантовой конденсированной материи играет роль плотности вакуумной энергии. Давайте начнем с «Теории Всего» для конденсированной материи. Основополагающая  микроскопическая физика жидкости или твердого тела, состоящего из $N$атомов, - квантовая механика. Система описывается $N$-частичной волновой функцией$\Psi \left( {{{\vec{r}}}_{1}},{{{\vec{r}}}_{2}}\ldots {{{\vec{r}}}_{N}} \right)$. Соответствующий многочастичный гамильтониан

\[H=-\frac{{{\hbar }^{2}}}{2m}\sum\limits_{i=1}^{N}{\sum\limits_{j=i+1}^{N}{U\left( {{{\vec{r}}}_{i}}-{{{\vec{r}}}_{j}} \right)}}\] (6) где $m$-масса «голого» атома.

В термодинамическом пределе, когда $V\to \infty $ и $N$макроскопически велико, возможно альтернативное описание системы в терминах квантованных полей, известное как вторичное квантование. Квантованные поля представляются бозонными или фермионными операторами уничтожения атомов $\psi (\vec{x})$. Многочастичный гамильтониан  (6) трансформируется в гамильтониан квантовой теории поля (КТП)

\[\begin{align} {{{\hat{H}}}_{QFT}}=\hat{H}-\mu \hat{N}=\int{d\vec{x}{{\psi }^{+}}(\vec{x})\left[ -\frac{{{\nabla }^{2}}}{2m}-\mu  \right]\psi (\vec{x})} \\ +\frac{1}{2}\int{d\vec{x}d\vec{y}U\left( \vec{x}-\vec{y} \right){{\psi }^{+}}(\vec{x}){{\psi }^{+}}(\vec{y})\psi (\vec{y})\psi (\vec{x})} \\ \end{align}\] (7)

Здесь $\hat{N}=\int{dx{{\psi }^{+}}(\vec{x})\psi (\vec{x})}$-оператор числа частиц (числа атомов), $\mu $- химический потенциал – множитель Лагранжа, введенный для учета сохранения числа атомов.

Можно показать, что вакуум в КТП определяется не гамильтонианом $\hat{H}$, а гамильтонианом \[{{\hat{H}}_{QFT}}=\hat{H}-\mu \hat{N}\]. Поэтому плотность энергии вакуума в КТП описании определяется термодинамическим потенциалом $E-\mu N$, который является вакуумным средним гамильтониана ${{\hat{H}}_{QFT}}$

\[{{\varepsilon }_{vac}}=\frac{1}{V}{{\left\langle {{{\hat{H}}}_{QFT}} \right\rangle }_{vac}}\] (8)

Гамильтониан (7) служит стартовой точкой для конструирования эффективной КТП, описывающей квазичастицы при низких энергиях и их вакуум.

3.2. Уравнение состояния для вакуума в конденсированной материи

Давайте проверим, что плотность энергии (8) является правильным выбором для плотности энергии вакуума. Сделаем это с помощью термодинамического  соотношения Гиббса-Духема, которое справедливо в термодинамическом пределе$N\to \infty $. Это соотношение утверждает, что если конденсированная материя находится в равновесии, то она подчиняется следующему соотношению между средней энергией $\left\langle {\hat{H}} \right\rangle $ и другими термодинамическими переменными: температурой $T$, энтропией $S$и числом частиц $N=\left\langle {\hat{N}} \right\rangle $, химическим потенциалом $\mu $ и давлением$p$:

\[E-TS-\mu N=-pv\] (9)

Применяя это соотношение к равновесному вакууму, т.е равновесному состоянию при $T=0$, мы получим соотношение (5) между плотностью энергии вакуума и его давлением

\[{{\varepsilon }_{vac}}=\frac{1}{V}{{\left\langle {{H}_{QFT}} \right\rangle }_{vac}}=\frac{1}{V}{{\left\langle {\hat{H}} \right\rangle }_{vac}}-\frac{1}{V}\mu {{\left\langle {\hat{N}} \right\rangle }_{vac}}=-{{p}_{vac}}\] (10)

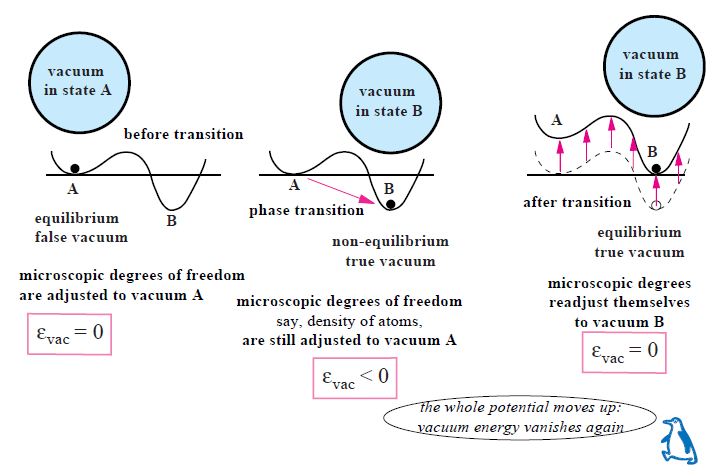
Рис.2. Сценарий в физике конденсированного состояния эволюции плотности энергии $\epsilon _{vac}$ физического вакуума фазового перехода первого рода равновесного состояния фальшивого вакуума в равновесное состояние истинного вакуума. До фазового перехода то есть в фальшивом, но равновесном вакууме должно быть $\epsilon _{vac} =0.$ В течении переходного периода микроскопические параметры вакуума изменялись на новые, соответствующие равновесному состоянию в котором условие $\epsilon _{vac} =0.$ не выполняется.

3.3 Термодинамика вакуума

Термодинамический анализ не зависит от микроскопической структуры вакуума и поэтому может быть применим к любому квантовому вакууму. Это утверждение следует из простого анализа равновесия поршня между квантовым вакуумом и пустым пространством (см. Рис.1). Сила действующая на поршень есть $F=-\frac{d{{E}_{vac}}}{dx}=-A\frac{d{{E}_{vac}}}{dV}=-A{{\varepsilon }_{vac}}$А, где $A$-площадь поршня. С другой стороны, сила, деленная на площадь, представляет давление вакуума. И мы приходим к уравнению состояния (5).

Таким образом, из термодинамики следует общее свойство:  вакуум ведет себя как среда с уравнением состояния (5). Это и не удивительно. Ведь выше мы видели, что такое уравнение состояния применимо к вакууму релятивистской квантовой теории поля (РКТП). Это показывает, что проблема вакуумной энергии может быть рассмотрена с более общей точки зрения, не ограничиваясь релятивистскими гамильтонианами, а включая и полевой подход. Кроме того, не существенно, включается или нет гравитация, т.е. является ли вакуум гравитирующим или нет.

Вакуумная энергия играет важную роль даже в отсутствие гравитации. Представим себе мир без гравитации, т.е. мир где метрические поля не входят в низко энергетический сектор, или мир, где ньютоновская константа всемирного тяготения $G=0$. В таком мире материя должна расширяться, благодаря давлению материи. Однако, сравнивая эту ситуацию с той, которая возникает в конденсированной материи, где роль вакуума играет основное состояние, а роль материи -  квазичастицы, мы увидим в разделе 8.1, что Вселенная в таком мире может быть стабилизирована вакуумным давлением, которое компенсирует давление материи.

Вместо заключения

Комментарии (4):

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.