Гипотеза Больших чисел явилась результатом исследований Поля Дирака в 1937 году. В тот период П.Дирак изучал отношения сил и параметров различных масштабов. Эти отношения выражаются большими безразмерными числами: около 40-ка порядков величины.

Владимир Авданин

Санкт-Петербург, Россия

Вступление

Так, например, отношение кулоновской силы к силе тяготения между протоном и электроном  принято обозначать через D_o:

${{D}_{o}}=\frac{{{F}_{C}}}{{{F}_{G}}}\,\,\approx \,2.27\cdot {{10}^{39}}$                                                    (1)

Согласно гипотезе Дирака, эквивалентность отношений различных величин является не простым совпадением, а обусловлено зависимостью фундаментальных физических постоянных от времени, т.е. от возраста Вселенной  [1,2].  Наиболее полное изложение проблемы можно найти  в работах [3, 4, 5]. В нашей статье основным постулатом является неизменность в ходе космологического расширения следующих величин:  Планковских единиц (массы, длины и времени), постоянной Планка, скорости света. Постоянство гравитационной постоянной будет показано как следствие принятого постулата. На этом основании выполнен сравнительный анализ двух космологических эпох - современной и Планковской (10^-43 секунды после Большого Взрыва). Предложены зависимости от времени таких физических величин и констант как: постоянная Хаббла, постоянная тонкой структуры, космологическая постоянная, масса, плотность, расстояние и др.  Сделан вывод о постоянстве скорости увеличения массы материи Вселенной, равной около 4 ∙ 10 ³⁵  kg/s  на протяжении всех эпох, начиная с Планковской.  Отмечено, что в ходе космологического расширения имеет место пропорциональное увеличение массы материи и массы, соответствующей темной энергии, в результате суммарная масса гравитационно-связанной Вселенной равна  нулю,  что не противоречит закону сохранения массы.

Радиус когерентности

   Прежде чем анализировать безразмерные большие числа Дирака, определимся с некоторыми понятиями, используемыми в данной статье. Основным из них является понятие радиуса гравитационной когерентности тела, имеющего массу. В результате существования антигравитации вакуума (темной энергии) гравитационное влияние тела, имеющего массу, хотя и распространяется бесконечно, но имеет вполне определенную границу действия в условиях темной энергии. Эту границу можно назвать границей  гравитационной когерентности (или связанности). Эта обстоятельство обусловлено существованием темной энергии во Вселенной. Как  показано в работах А.Д.Чернова [6],  на некотором расстоянии  R_o от центра масс сила отталкивания, создаваемая темной энергией  и сила притяжения, создаваемой на том же расстоянии суммарной массой, заключенной в сфере данного радиуса, станут равными. Данный радиус  R_o – это радиус гравитационной когерентности массы, который  зависит от массы и определяет  границу ее гравитационного влияния.  Из условия равенства сил притяжения и отталкивания следует, что радиус  R_o  равен:

${{R}_{o}}={{\left( \frac{G\,{{m}_{{}}}}{H_{o}^{2}{{\Omega }_{\Lambda }}} \right)}^{1/3}}={{\left( \frac{3{{m}_{{}}}}{8\pi \,{{\Omega }_{\Lambda }}\,{{\rho }_{c}}} \right)}^{1/3}}$                                               (2)

здесь  Ω_Λ – плотность темной энергии в единицах критической плотности ρ_c , H_o – постоянная Хаббла, G– гравитационная постоянная. Обозначим через ρ_oсреднюю плотность материи, заключенную в сфере радиуса R_o.  Назовем ее плотностью когерентности:

${{\rho }_{o}}=\,\,\frac{3H_{o}^{2}}{4\pi G}{{\Omega }_{\Lambda }}=2{{\rho }_{V}}\,\approx \,1.3\cdot {{10}^{-26}}kg/{{m}^{3}}$                                        (3)

Здесь  ρ_V≈ 6.6 ∙ 10^-27 kg/m³ – плотность вакуума (темной энергии). Итак, плотность когерентности равна удвоенному значению плотности темной энергии. Введем обозначение:                    

 $\,{{\omega }_{o}}={{H}_{o\,}}\sqrt{{{\Omega }_{\Lambda }}}$                                                                (4)

и запишем выражения (2) и (3)   в следующей форме:

_{${{R}_{o}}={{\left( \frac{G\,{{m}_{{}}}}{\omega _{o}^{2}} \right)}^{1/3}}$}                                                             (5)

Выражения (2-5) пригодятся нам при дальнейшем рассмотрении. Здесь величина ω _o≈ 1.9 ∙ 10 ^-18 s^-1 является константой и имеет размерность угловой частоты. Напомним, что в  отличие от радиуса R_oдля каждой массы mсуществует гравитационный (или критический) радиус R_G, который зависит от ее значения:

 ${{R}_{G}}=\frac{2G\,{{m}_{{}}}}{c_{{}}^{2}}$                                                              (6)                                         

Гравитационный радиус R_G  и радиус когерентности R_o для заданного значения массы связаны  следующим выражением:

${{R}_{G}}=\frac{2\omega _{o}^{2}}{{{c}^{2}}}R_{o}^{3}$                                                              (7)

что показано на рис.1.   В случае равенства радиусов R_Gи R_o имеем:

$r_{og}^{{}}={{R}_{G}}={{R}_{o}}=\frac{c}{\omega _{o}^{{}}\sqrt{2}}\approx \,1.1\cdot {{10}^{26}}m\approx \,11.6\,\,Gyr$                          (8)

Таким образом,  для сферы с радиусом, равным 11.6 миллиардов световых лет, характерно равенство критической плотности и плотности когерентности, и, значит, для нее средняя плотность материи в единицах критической плотности  равна  Ω_M = Ω_Λ = 0,5,  а масса такой области  Вселенной составит:   

$M_{og}=\frac{{{c}^{3}}}{H_{o}^{{}}\,G\sqrt{8{{\Omega }_{\Lambda }}}}$                                                     (9)

Сделаем предположение о том, что именно в области, соответствующей радиусу r_og, происходит смена ускоренного расширения Вселенной на замедленное (в соответствии с временной шкалой после Большого Взрыва – наоборот, сначала было замедление, а потом ускорение). Это подтверждается последними данными по  сверхновой  SN 1997ff   [9]. Именно на этом рубеже гравитационный радиус «обгоняет» радиус когерентности Вселенной.

 Рассмотрим далее характерные расстояния во Вселенной, связанные с величинами ρ_oи ω_o.  За время,  равное T_U= 1/ω_o, луч света пройдет расстояние:

                                                              ${{R}_{U}}\,=\,\frac{c}{{{\omega }_{o}}}\,=\sqrt{\frac{3}{\Lambda }}\approx \,1.56\cdot {{10}^{26}}m\approx \,16.3\,\,Gyr$          (10)                                         где Λ – космологическая постоянная.  Это расстояние соответствует азимутальной (тангенциальной) скорости, равной скорости света, и, как будет показано далее, является радиусом когерентности современной Вселенной.  Время T_U= 1/ω_oпосле Большого Взрыва определим как возраст Вселенной, соответствующий cовременной эпохе, в отличие от t– текущего возраста в ходе расширения.  Отсюда с учетом (7) гравитационный радиус Вселенной  в современную эпоху  равен R_G = 2R_U ≈ 3,12 ∙ 10 ^{26 m} ≈ 32.6 Gyr и находится за пределами гравитационно-связанной сферы (т.е. эта область более не принимает активного участия в «жизни» наблюдаемой части Вселенной, не имея с ней причинно-следственных связей). Для каждой эпохи существует свое значение радиуса Хаббла, на котором материя достигает радиальной скорости света в ходе расширения Вселенной:

${{R}_{H}}(t)=\frac{C}{{{H}_{o\,}}(t)}=\,\,t\sqrt{{{\Omega }_{\Lambda }}}\,\,$                                             (11)                    

В современную эпоху R_H ≈ 1.32 ∙ 10 ²⁶ m  ≈ 13.8 Gyr   при  условии, что  H_o ≈ 70 (km/s)/Mpc.  Зависимость рассматриваемых расстояний от времени является линейной и представлена на рис.2. Теоретически можно предположить, что масштабы всей Вселенной значительно больше масштабов наблюдаемой ее части. Так, за период, равный T_∞ = 2π /ω_o, луч света пройдет расстояние:

                         ${{R}_{U}}\,=\,\frac{2\pi \,c}{{{\omega }_{o}}}\,\approx \,105\,\,Gyr$

Безразмерные числа

Наши дальнейшие рассуждения будем основывать на  постулате о постоянстве Планковских единиц.   Найдем отношение космологических и Планковских величин, а именно:  величины ω_oи Планковской частоты ω_pl , далее -  величины  R_U и  Планковской длины l_pl, а также -  возраста Вселенной T_U и Планковского времени t_pl.  Получим простую зависимость:

$\frac{{{\omega }_{pl}}}{{{\omega }_{o}}}=\frac{{{R}_{U}}}{{{l}_{pl}}}=\,\frac{{{T}_{U}}}{{{t}_{pl}}}=\sqrt{\frac{3\,{{c}^{3}}}{\,\Lambda \hbar \,G\,}}$                                          (12)

Введем обозначение:

                                                                                                    ${{D}_{U}}=\,\frac{3\,{{c}^{3}}}{\,\Lambda \hbar \,G\,}$                                                  (13)

и дополним  выражение (12) следующим очевидным отношением: D_U= (R_o(pl) /  l_pl)³, где  R_o(pl) – это радиус  когерентности Планковской массы. Отсюда имеем:   

                                                   ${{D}_{U}}={{\left( \frac{{{\omega }_{pl}}}{{{\omega }_{o}}} \right)}^{2}}={{\left( \frac{{{R}_{U}}}{{{l}_{pl}}} \right)}^{2}}=\,{{\left( \frac{{{T}_{U}}}{{{t}_{pl}}} \right)}^{2}}={{\left( \frac{{{R}_{o(pl)}}}{{{l}_{pl}}} \right)}^{3}}\approx 9.2\cdot {{10}^{121}}$                          (14)

Итак, мы получили еще одно большое число Дирака, которое простым образом связывает физические параметры, характеризующие  современную и Планковскую эпохи соответственно. Пропорциональные отношения различных физических фундаментальных констант, соответствующих  двум эпохам, - современной и Планковской -  можно объяснить одновременным изменением параметров в процессе расширения Вселенной, т.е. одинаковой зависимостью от времени. В современную космологическую эпоху эта зависимость выражается числом D_U и его производными значениями.  Найдем два производных значения:

$D_{U}^{1/2}=\,{{\left( \frac{3\,{{c}^{3}}}{\,\Lambda \hbar \,G\,} \right)}^{1/2}}\approx 9.6\cdot {{10}^{60}},\,\,\,D_{U}^{1/3}=\,{{\left( \frac{3\,{{c}^{3}}}{\,\Lambda \hbar \,G\,} \right)}^{1/3}}\approx 4.5\cdot {{10}^{40}}$

 

Космологическая постоянная Λ

Из (12)  следует:                                                            

  $\Lambda =\frac{3\,}{\,l_{pl}^{2}\,}\,\,{{\left( \frac{{{t}_{pl}}}{{{T}_{U}}} \right)}^{2}}$                                                     (15)

- выражение для константы в современную эпоху (t = T_U) . Для Планковской эпохи (t=  t_pl)  имеем:      

          ${{\Lambda }_{0}}=\frac{3\,}{\,l_{pl}^{2}\,}$                                                         (16)

Таким образом, космологическая постоянная с момента окончания Планковской эпохи к настоящему времени уменьшилась от значения порядка  10⁷⁰ m^-2   до 10^-52 m^-2, т.е. на 122 порядка величин. Из (15) и (16) получим:

 ${{D}_{U}}=\frac{{{\Lambda }_{0}}}{\,\Lambda \,}$                                                      (17)

Зависимость константы от времени выглядит  так:

   $\Lambda (t)\,=\frac{3}{{{c}^{2}}{{t}^{2}}}$                                                    (18)

Таким образом, что в ходе космологического расширения константа Λ уменьшается пропорционально квадрату времени (см. рис.3).   

Постоянная тонкой структуры.

После Планковской эпохи началась Эпоха великого объединения, которая длилась между 10^-43 и 10^-35 s  после Большого Взрыва. Вселенная расширяется и охлаждается после Планковской эпохи, и различные типы взаимодействий начинают отличаться друг от друга по величине.  После Эпохи великого объединения  началась Эпоха раздувания (инфляции) - между 10^-35 и 10^-32 s после Большого Взрыва. В эту эпоху Вселенная все еще преимущественно заполнена излучением, начинают образовываться кварки, электроны и нейтрино. Далее следует Эпоха электрослабых взаимодействий - между 10^-32 и 10^-12 s после Большого Взрыва. Электромагнитные взаимодействия и слабые взаимодействия пока представляют собой единое электрослабое взаимодействие. В теории электрослабого взаимодействия показано, что значение постоянной тонкой структуры (сила электромагнитного взаимодействия) зависит от характерной энергии рассматриваемого процесса. Утверждается, что постоянная тонкой структуры логарифмически растёт с увеличением энергии. Наблюдаемое значение постоянной тонкой структуры верно при энергиях порядка массы электрона. Мы предполагаем, что  такое  значение постоянной α сформировалось  именно на рубеже двух эпох:  Эпохи инфляции  и Эпохи электрослабых взаимодействий.

Большое число, учитывающее постоянную тонкой структуры α, и равное exp(1/α) было предложено в 1948 году [7]. Представляется возможным  использовать данное большое число для выражения  зависимости  константы α от времени τ, соответствующего концу Эпохи инфляции и началу формирования единого электрослабого взаимодействия. Для этого введем величину, равную логарифму времени τ, выраженного в единицах Планковского времени. Зависимость выглядит так:

                                                        $\,{{e}^{1/\alpha }}=\frac{\sqrt{D_{U}^{{}}}}{\ln (\tau /\,{{t}_{pl}})}$                                                     (19)

отсюда   выразим время формирования современного значения константы α ≈ 0.00729735..:

 ${{\tau }_{\alpha }}\,=\,\,{{t}_{pl}}\,{{e}^{\sqrt{D_{U}^{{}}}/{{e}^{1/\alpha }}}}\approx 3\cdot {{10}^{-31}}s$                                        (20)

после Большого Взрыва, что соответствует концу Эпохи инфляции, что и следовало показать. Значение константы в любой момент времени tпосле Большого взрыва можно найти по формуле:

_{$\,\alpha ={{\left[ \ln \frac{\sqrt{D_{U}^{{}}}}{\ln (t/\,{{t}_{pl}})} \right]}^{-1}}$}                                                 (21)

Современное значение константы также можно найти  по следующей эмпирической формуле:

_{$\,\alpha =2{{\left[ \ln D_{U}^{{}}\frac{{{r}_{e}}}{{{\lambda }_{e}}} \right]}^{-1}}$}                                                    (22)

где  r_e/ λ_e  - отношение классического радиуса электрона к его комптоновской длине волны.

   

Плотность материи и энергии

В общем виде плотность вакуума (темной энергии) равна:

${{\rho }_{\begin{smallmatrix} V \\ \end{smallmatrix}}}=\frac{\Lambda {{c}^{2}}\,}{8\pi \,G\,\,}$                                                           (23)

Отсюда  с учетом выражения для космологической константы  (16)  получим абсолютное значение плотности темной энергии в Планковскую эпоху:   

${{\rho }_{\begin{smallmatrix}  Vo \\ \end{smallmatrix}}}=\frac{3{{c}^{5}}\,}{8\pi \,\hbar {{G}^{2}}\,\,}$ (24)

Отсюда следует:                                                                 $\frac{{{\rho }_{Vo}}\,\,}{{{\rho }_{V}}\,}={{D}_{U}}$                                                           (25)

Можно записать и так:                                            ${{\rho }_{V}}(t)\,={{\rho }_{Vo}}{{\left( \frac{{{t}_{pl}}}{t} \right)}^{2}}=\frac{3}{8\,\pi G\,{{t}^{2}}}$                                           (26)                

Это означает, что в процессе расширения Вселенной плотность темной энергии уменьшается пропорционально квадрату возраста Вселенной t, выраженного в секундах.  Чтобы найти относительное значение плотности темной энергии в Планковскую эпоху в единицах критической плотности (имевшей место на тот момент), определим эту критическую плотность. Запишем значение критической плотности для массы M:

 ${{\rho }_{g}}=\,\frac{3c_{{}}^{6}}{32\pi \,M_{{}}^{2}{{G}^{3}}}$                                                     (27)

В качестве  М  примем  m_pl (Планковскую массу) и получим критическую плотность ρ_coВселенной в Планковскую эпоху (при условии постоянства с и G):  

${{\rho }_{c\,o}}=\,\frac{3c_{{}}^{5}}{32\pi \,\hbar {{G}^{2}}}$                                                    (28)

и также получим зависимость критической плотности от времени:                                                                                    

                                                                                ${{\rho }_{c}}(t)\,={{\rho }_{co}}{{\left( \frac{{{t}_{pl}}}{t} \right)}^{2}}=\frac{3}{32\,\pi G\,{{t}^{2}}}$                                             (29)                

Можем записать выражение в общем виде для относительной плотности:

                                 ${{\Omega }_{\Lambda }}=\,\,\,{{\left( \frac{r\,dt}{t\,dr} \right)}^{2}}$                                                      (30)

где r – это размер той области, в масштабах которой мы определяем среднее значение плотности,  его значение находится в пределах 2 l_pl≤ r≤ R_G = 2 R_U (т.е. определяется диапазоном значений горизонта событий в ходе расширения Вселенной). Отсюда относительное значение плотности, соответствующее гравитационному радиусу (как в Планковскую эпоху, когда  r= 2 l_pl , так и в современную эпоху, когда r= 2 R_U ), равно:   Ω_Λ= 4.0.

Аналогично, относительное значение плотности, соответствующее радиусу когерентности (как в Планковскую эпоху, когда  r=  l_pl , так и в современную эпоху, когда r=  R_U), будет равно: Ω_Λ= 1.0. 

В современную эпоху относительная  плотность темной энергии в наблюдаемой части Вселенной, ограниченной радиусом Хаббла (r= R_H), в соответствии с (30) составляет:   

${{\Omega }_{\Lambda }}({{R}_{H}})=\,\,\,\frac{R_{H}^{2}}{T_{U}^{2}\,{{c}^{2}}\,}\approx \,0.72\div \,0.73$                                           (31)

Зависимость относительной плотности от r в отдельно взятую эпоху показана на рис.4 в верхней части графика. Зависимость критической плотности и плотности темной энергии в абсолютном в выражении  показана в нижней его части.

Закон Хаббла

  С учетом (4 и 30):

  ${{H}_{o\,}}=\frac{{{\omega }_{o}}}{\sqrt{{{\Omega }_{\Lambda }}}}=\frac{dr}{r\,dt}$                                                                   (32)

Для радиуса когерентности всегда будет верным Ω_Λ = 1 и  H_o= ω_o. Для современной эпохи имеем табличное значение постоянной  Хаббла:

             ${{H}_{o\,}}=\,\frac{1}{{{T}_{U}}\sqrt{{{\Omega }_{\Lambda }}}\,}\approx 70\,(km/s)Mpc\,\,\,\,\,\,$

Постоянная Хаббла не является, строго говоря, постоянной величиной, т.к. в разных областях Вселенной даже в одну эпоху значение этого параметра зависит от Ω_Λ. А величина ω_o зависит только от времени. Поэтому закон Хаббла логично представить в соответствии с (32) следующим образом:

       $\frac{dr}{\,dt}=r\frac{{{\omega }_{o}}(t)}{\sqrt{{{\Omega }_{\Lambda }}}}$                                                                   (33)

что в принципе ничего не меняет, кроме акцентов, однако может объяснить расхождения в расчетных  данных по константе Хаббла, причем расхождения именно в √Ω_Λ раз, что вполне объяснимо, если посмотреть на формулу.

Масса

Оценка значения  массы  видимой Вселенной зависит от того,  что  собой представляет  радиус         ${{R}_{U}}\,$ ≈ 1.56 ∙ 10 ²⁶  m ≈ 16.3 Gyr в выражении (10). Определяя R_U  как радиус когерентности, получим с учетом (2 и 5)  значение полной массы Вселенной:

${{M}_{U}}\,=\frac{8\pi \,{{\rho }_{V}}R_{U}^{3}}{3}=\frac{{{c}^{3}}}{G\omega _{o}^{{}}}\approx 2.1\cdot {{10}^{53}}\,kg$                                               (34)

Найдем массу темной энергии в пределах радиуса R_U. Поскольку масса темной энергии в пределах произвольной сферы равна эффективной гравитирующей плотности вакуума  ε_G = - 2ρ_v, умноженной на объем данной сферы [6], то получим:

${{M}_{\Lambda }}\,({{R}_{U}})=\frac{4\pi \,{{c}^{3}}}{3\,\omega _{o}^{3}}\,\cdot \,(-2{{\rho }_{V}})=\,-\frac{{{c}^{3}}}{G\omega _{o}^{{}}}\,\approx -2.1\cdot {{10}^{53}}\,kg$                                    (35)

Сравнивая выражения (33) и (34) имеем:  M_U = - M_Λ. Это значит, что суммарная масса Вселенной, как целостного, гравитационно-связанного объекта, ограниченного радиусом когерентности R_U≈ 16.3 Gyr, равна M_U + M_Λ = 0, т.е. нулю. Допущение существования отрицательных масс ведёт к определённым сложностям в интерпретации принципа эквивалентности и закона сохранения импульса. Тем не менее, равенство нулю суммарной массы точно определяет границу области гравитационной когерентности любого объекта. При увеличении объема плотность массы материи и излучения уменьшаются с разной скоростью, пропорционально третьей и четвертной степени радиуса соответственно. Но, имея в виду изменение во времени, мы говорим о равном увеличении  составляющих  массы  (M_Uи M_Λ)  с течением времени, и предполагаем существование «нулевого баланса» массы/энергии на границе когерентности  Вселенной на всех стадиях расширения после Большого взрыва.  В Общей теории относительности (ОТО) допускается существование локальных пространственных областей с отрицательной плотностью энергии-импульса. Часть Вселенной (в пределах сферы радиуса R_U) охвачена силами доминирующей гравитации, - это своего рода «гравитирующее ядро». Вторая часть - между сферами радиусов R_U и R_g-  охвачена силами доминирующей антигравитации, причем, 2R_U= R_g. Значению R_U соответствует суммарная нулевая масса.  Но R_g- гравитационный радиус, «изнутри» которого действует антигравитация. Остается предположить, что область R_g - это область сверхвысокого давления, т.е. сингулярности, которая вышла за пределы гравитационно-связанной Вселенной.

Далее. Найдем отношение массы Вселенной к Планковской массе. Следующие выражения являются очевидными:

$\frac{{{M}_{U}}}{{{m}_{pl}}}=-\frac{{{M}_{\Lambda }}}{{{m}_{pl}}}=\frac{{{T}_{U}}}{{{t}_{pl}}}\,\,\,\,\,\,\text{}\,\,\,\,\text{  }{{\left( \frac{{{M}_{U}}}{{{m}_{pl}}} \right)}^{2}}\,={{\left( \frac{-{{M}_{\Lambda }}}{{{m}_{pl}}} \right)}^{2}}={{D}_{U}}$                             (36)

Второе выражение можно записать и в такой форме:    

         ${{M}_{U}}(t)\,={{m}_{pl}}\frac{t}{{{t}_{pl}}}=\left( \frac{{{c}^{3}}}{G} \right)\,\,t$                                                 (37)      

Таким образом, масса Вселенной (как и модуль массы темной энергии) растет прямо пропорционально времени.  На  рис. 6 показана зависимость массы Вселенной от  ее возраста.

Выражение (37) формально напоминает предположение Дирака [2]:            

     $G=\left( \frac{{{c}^{3}}}{{{M}_{U}}} \right)t$                                                    (38)

где  G, как предполагается,  - величина переменная, M_U  - величина постоянная,   t - возраст Вселенной в секундах. Предлагаемое нами выражение (37) по смыслу противоречит последнему выражению, т.к. в рамках наших рассуждений: M_U~ t и  G= const,  что не противоречит ОТО,  а  в соответствии с предположением Дирака  M_U~ t²  и  G~ 1/t,   что   противоречит постулатам ОТО. Надо отметить, что в рамках обеих гипотез будет верным GM_U~ t и  c = const.   

Далее.  Предположим, что  существует минимально возможная в природе «элементарная» масса. В контексте нашего изложения выражение для нее может иметь вид:

    _{${{m}_{\min }}=\frac{\hbar \,{{\omega }_{o}}}{{{c}^{2}}\,}$}                                                          (39)

Очевидно, что                                                            

   $\,\frac{{{M}_{U}}}{{{m}_{\min }}}\,\,=\,{{\left( \frac{{{T}_{U}}}{{{t}_{pl}}} \right)}^{2}}={{D}_{U}}$                                                (40)

отсюда зависимость минимальной массы от времени имеет вид: 

 ${{m}_{\min }}(t)={{m}_{pl}}\,\,\frac{{{t}_{pl}}}{t}\,=\frac{\hbar }{t\,{{c}^{2}}}$                                         (41)

Из (40 и 41) также следует:

                                                                        ${{m}_{pl}}^{2}={{M}_{U}}\,(t)\,\,{{m}_{\min }}(t)$                                                    (42)

и, следовательно, известное большое число Дирака из (1) примет вид:  

 ${{D}_{o}}=\,\alpha \frac{{{M}_{U}}{{m}_{\min }}}{{{m}_{p}}\,{{m}_{e}}\,}$                                       (43)

где  m_pи  m_e - массы протона и электрона соответственно. Заметим, что в Планковскую эпоху масса Вселенной и минимальная масса были равны Планковской массе (см. рис.6):                                               

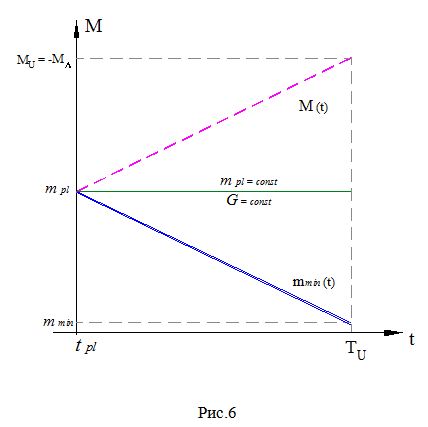
Существуют  предложения ввести энергетическое большое число Дирака, например, в [8].  Однако, если и существует энергетическое большое число Дирака, то в контексте наших рассуждений оно выглядит следующим образом:

$\,\frac{{{M}_{U}}\,{{}^{2}}}{{{m}_{\min }}{{}^{2}}}=\,\frac{{{M}_{U}}}{{{m}_{\min }}}={{D}_{U}}$                                                           (44)

С учетом последних выражений можно сделать вывод о постоянстве скорости  увеличения массы материи во Вселенной,  начиная с Планковской эпохи:

$\theta \,=\frac{dM}{dt}=\frac{{{c}^{3}}}{G}=const$                                                       (45)

Можно записать:                                   

        $\theta \,={{H}_{pl\,}}{{m}_{pl}}={{H}_{o\,}}{{M}_{H}}$≈ 4 ∙ 10 ³⁵  kg/s                                                (46)

где   M_H  - масса Вселенной в объеме сферы радиуса Хаббла:

 ${{M}_{H}}\,=\frac{{{c}^{3}}}{GH_{o}^{{}}}$                                                                (47)

Отметим одно замечательное свойство найденного значения массы Вселенной (34). Из выражения (12), в частности,  следует:           

         ${{M}_{U}}={{\rho }_{pl}}\,l_{pl}^{2}\,{{R}_{U}}$,                                                            (48)

т.е.  масса  Вселенной  равна массе эквивалентной «струны», имеющей поперечное сечение, равное   квадрату Планковской длины, плотность, равную Планковской плотности,  и длину, равную радиусу когерентности Вселенной. Здесь мы имеем косвенное подтверждение так называемой струнной теории мироздания.

Отметим также одно замечательное свойство предложенного значения минимальной массы (39). Если предположить существование гипотетической частицы такой массы (около 2.26 ∙ 10 ^-69  kg), то ее  комптоновская длина волны будет равна:

 ${{\lambda }_{U}}=\frac{2\pi \,\hbar }{c{{m}_{\min }}\,}=\,2\pi {{R}_{U}}$(49)

т.е. равна «длине окружности» всей Вселенной. Такое предельное значение комптоновской длины, как известно,  приписывается частице «квинтэссенции», которая альтернативна идее темной энергии.   

Гравитационная постоянная G

  Из выражения (12)   получим:

_{$\omega _{o}^{2}=\frac{G\,{{M}_{U}}}{R_{U}^{3}}\,\,\,\,\,\text{}\,\,\,\,\,\,\omega _{pl}^{2}=\frac{G\,{{m}_{pl}}}{l_{pl}^{3}}$}                   (50)

Решая эти уравнения совместно,  делаем принципиальный  вывод,что   в   процессе   расширения Вселенной гравитационная постоянная   G  от времени не зависит,  G = const, что соответствует положениям Общей теории относительности,  и  нашему  изначальному  постулату  о  постоянстве Планковских единиц.

      Физический смысл большого числа D_U

Таким образом,  наряду с известным безразмерным числом D_o≈ 2.27 ∙ 10 ³⁹, мы нашли  значение еще одного Большого числа Дирака,   равного  D_U ≈ 9.2 ∙ 10¹²¹.    Нетрудно показать, что безразмерное число D_U - есть отношение силы гравитационного взаимодействия между материей Вселенной, имеющей массу  М_U  и темной энергией Вселенной, имеющей массу М_Λ, к силе  кулоновского взаимодействия между двумя Планковскими зарядами: 

                                                                     $\,D_{U}^{{}}=\,\,\frac{{{F}_{G}}({{M}_{\Lambda }},\,{{M}_{U}})}{{{F}_{C}}({{q}_{pl}},\,{{q}_{pl}})}$                                                      (51)

Таким образом,  логично предположить, что Большой взрыв – это результат столкновения двух трехмерных бран, имеющих планковский заряд, что и определило в дальнейшем пропорции крупномасштабной структуры Вселенной.  Кроме того, в  соответствии с (22) число D_U также с большой точностью выражает отношение  корпускулярных и волновых свойств электрона в современную эпоху:

_{$\,D_{U}^{{}}=\frac{{{r}_{e}}}{{{\lambda }_{e}}}\,{{e}^{{2}/{\alpha }\;}}\,=\frac{2\pi }{\alpha }{{e}^{{2}/{\alpha }\;}}$}                                                (52)

                  

Заключение

Итак, в подтверждение гипотезы Дирака резюмируем зависимость различных величин от времени:

 

 

Радиус когерентности Вселенной	${{R}_{U}}(t)\,=\,c\,t$
Гравитационный радиус Вселенной	${{R}_{g}}(t)=2R_{U}^{{}}(t)$
Радиус Хаббла	${{R}_{H}}(t)=\frac{}{{{H}_{o\,}}(t)}=\,t\sqrt{{{\Omega }_{\Lambda }}}\,\,$
Масса материи	${{M}_{U}}(t)=\,\left( \frac{{{c}^{3}}}{G} \right)\,t$
Масса темной энергии	${{M}_{\Lambda }}(t)=\,-\left( \frac{{{c}^{3}}}{G} \right)\,t$
Минимальная (элементарная) масса	${{m}_{\min }}(t)=\frac{\hbar }{t\,{{c}^{2}}\,}\,$
Плотность темной энергии	${{\rho }_{V}}(t)\,=\frac{1}{{{t}^{2}}}\left( \frac{3}{8\,\pi G\,} \right)$
Минимальная угловая скорость	${{\omega }_{0}}(t)=\,\,\frac{1}{t}$
Космологическая постоянная	$\Lambda (t)\,={{\Lambda }_{0}}{{\left( \frac{{{t}_{pl}}}{t} \right)}^{2}}=\frac{3}{{{c}^{2}}{{t}^{2}}}$
Постоянная Хаббла	${{H}_{o\,}}(t)=\,\frac{1}{t\,\sqrt{{{\Omega }_{\Lambda }}}\,}$
Скорость увеличения массы материи во Вселенной	$\theta \,=\frac{{{c}^{3}}}{G}=\,const$
Скорость света	c = const
Гравитационная постоянная	G = const
Планковские единицы	(ħ, l pl,tpl, m pl,q pl)= const.

 

RESUME  

 

 The evolution of fundamental constants

 

V. V. Avdanin

 

According to the Dirac large numbers hypothesis (LNH) extremely large numbers which characterize the relations between forces and parameters of various scales should be connected with the age of the Universe. This dependence should result in the change of fundamental constants with the lapse of time.  The permanence of Planck units (of mass, length and time), the Planck constant, light velocity, and the gravity constant in the course of cosmological expansion constitute  the main postulate discussed in this article.  A comparative analysis of two cosmological epochs – the modern one and the Planck epoch (10^-43 seconds after the Big Bang) – was prepared on this basis. At the same time the author suggests a time dependence of such physical values and constants as:  the Hubble constant, the fine-structure constant, the cosmological constant, mass, density, distance, etc. and determines the values of the relative dark energy density in various epochs.   The author comes to a conclusion about the constancy of the mass of Universe increase rate which is equal to the product of the mass of Universe and the Hubble constant (taken from a certain epoch). The rate is about  4 ∙ 10 ³⁵  kg/s, and it has not been changing during all the epochs since the Planck epoch. The author notes that the proportional increase of matter mass and the mass corresponding to the dark energy takes place in the course of the cosmological expansion. As a result, the total mass of gravitationally bound Universe is equal to zero, which does not contradict to the principle of mass conservation.

 

Список литературы

1.      P. A. M. Dirac.  A New Basis for Cosmology // Proc. R. Soc. Lond. A. — 1938. — Т. 165. — С. 199-208.

2.      P.A.M. Dirac. Cosmological Models and the Large Numbers Hypothesis. Proceedings of the Royal Society of London, vol. A338, N1615 pp. 439-446. DOI:10.1098/rspa.1974.0095.

3.      V. E. Shemi-Zadah.(2002). Coincidence of Large Numbers, exact value of cosmological parameters and their analytical representation. arxiv: gr-qc/0206084.

4.      Ross A. McPherson.(2008). The Numbers Universe: An Outline of the Dirac/Eddington Numbers as Scaling Factors for  Fractal, Black Hole Universes, EJTP 5, No. 18, pp. 81-94.

5.      Saibal Ray, Utpal Mukhopadhyay, Partha Pratim Ghosh: Large Number Hypothesis: A Review arXiv:0705.1836v1.

6.      А.Д. Чернов. Темная энергия вблизи нас. ГАИШ МГУ.

7.      E. Teller (1948). On the change of physical constants. Physical Review, vol.73 pp. 801-802.  

 DOI:10.1103/PhysRev.73.801.

8.      J. Casado (2004). Connecting Quantum and Cosmic Scales by a Decreasing-Light-Speed Model. arxiv: astro-ph/0404130 [astro-ph].

9.      The Farthest Known Supernova: Support for an Accelerating Universe and a Glimpse of the Epoch of Deceleration. arXiv:astro-ph/0104455v1.pdf  27 Apr 2001.

Администрация сайта не имеет никакого отношения к автору этой работы и может не разделять его мнения, а только публикует его статью.

Комментарии (2):

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.