В статье рассказывается о протяженных объектах - суперсимметричных струнах, которые, возможно, представляют собой наиболее фундаментальную структуру во Вселенной. В рамках современной физической картины мира предпринимаются вполне серьезные попытки отыскать те фундаментальные объекты, из которых можно было бы «сложить» все остальное. Анализировать при этом следует микромир, поскольку начиная с уровня кварков и лептонов мы примерно представляем себе, как более элементарные объекты комбинируются в более сложные. Но насколько осмысленным является дробление материи на все более элементарные составляющие? Каковы принципы, лежащие в основе поисков фундаментальных объектов, и есть ли конец этим поискам?

Введение

Сначала попытаемся описать, в каких терминах ставится задача и тем самым - в каких терминах исследователи ищут ее решение.

Первоначальной основой для построения любой физической теории служит наблюдаемый мир, и успех или неуспех теории определяется из сравнения ее с наблюдениями, с экспериментом. Однако, по мере продвижения в область все более фундаментальных и все менее непосредственно наблюдаемых явлений, значительную роль начинает играть математическая структура теории. Конечно любая теория должна быть математически корректной, но оказывается, что достичь та-кой корректности тем труднее, чем на большую общность претендует данная теория. Природа как бы сопротивляется произвольным построениям и требует, чтобы мы угадали ту, по всей видимости, единственную, наиболее фундаментальную структуру. Такую структуру также принято называть теорией. Таким образом, слово теория используется в двух значениях. Во-первых - это конкретный аппарат для описания того или иного объекта физической реальности, имеющий определенный набор уравнений, законов и правил. Во-вторых, - это именно та искомая сущность, которую нужно сначала отыскать, а потом научиться описывать в рамках конкретной теории в первом смысле этого слова.

Таким образом, развитие фундаментальной физики идет рука об руку с познанием математических структур, которые должны присутствовать в точной науке. Хорошо известным примером служит классическая теория гравитации, или общая теория относительности Эйнштейна. Согласно этой теории вся наблюдаемая в настоящий момент Вселенная, в космическом масштабе, - просто решение системы определенных уравнений, так называемых уравнений Эйнштейна. Но для того, чтобы эти уравнения сформулировать, их автору пришлось разработать целый ряд аспектов неевклидовой (римановой) геометрии. При этом математическая состоятельность уравнений требует, чтобы материя подчинялась определенным законам: она не может быть распределена в пространстве произвольно, и ограничения на ее поведение возникают из одной только математической корректности.

Обычная струна с закрепленными концами колеблется так, что на ее длине укладывается целое число полуволн. Поэтому на любой струне можно получить не одно колебание, а целый набор частот, которые называются гармониками.

Другой замечательный пример того, как требования математики позволяют даже предсказывать физические эффекты, - теория электромагнетизма. Описывающие его уравнения носят имя Максвелла. Формулируя в середине XIX века эти уравнения, Максвелл имел целью отразить в них все известные тогда сведения об электромагнетизме. Сделав это, он увидел, что уравнения оказались математически противоречивы (приводят к равенству 1 = 0). Максвеллу пришлось модифицировать уравнения так, чтобы восстановить их корректность. И оказалось, что именно такие модифицированные уравнения допускают невероятное по тем временам явление: существование электромагнитного поля, распространяющегося сколь угодно далеко от источника, то есть электромагнитных волн! Таким образом, электромагнитные волны были предсказаны, исходя только из анализа математических уравнений. Этот эпизод из истории науки способствует восприятию мира как реализованных решений каких-то уравнений; дело лишь за тем, чтобы угадать правильные уравнения.

Единая теория

Вернемся к проблеме поиска наиболее фундаментальных объектов в микромире. От кандидатов на эту должность требуется прежде всего способность объяснить единую основу всех взаимодействий в Природе. Их четыре: гравитационное (как раз то, которое описывается уравнениями Эйнштейна), электромагнитное (в той или иной степени всем знакомое), слабое и сильное (играющие существенную роль в микромире). Хорошо понято, каким образом при определенных физических условиях - на ранних этапах развития Вселенной - слабое и электромагнитное взаимодействия образовывали единое электрослабое взаимодействие. Это явление описывает теория Вайнберга - Салама, отмеченная Нобелевской премией по физике 1979 года. Мало сомнений в том, что в еще более ранние моменты жизни Вселенной сильное взаимодействие также образовывало единую сущность вместе с двумя другими.

Струна со свободными концами тоже способ­на колебаться, хотя и несколько иначе, чем зак­репленная струна. В этом легко убедиться, подбросив в воздух кусок упругой стальной про­волоки или металлическую линейку. Поведение такой «свободной струны» позволяет понять, как колеблются фундаментальные физические объекты - разомкнутые и замкнутые стру­ны.

Мысль, что все взаимодействия имеют единую природу, представляет собой важнейший принцип, который служит организующим началом в построении фундаментальных физических теорий. Следует ожидать, что и гравитационное взаимодействие - весьма, надо сказать, непохожее на остальные - в конечном итоге должно объединиться с ними. Но здесь нас поджидает неприятный сюрприз.

Дело в том, что, когда говорят о построении фундаментальной физической теории, имеют в виду, конечно, квантовую теорию, которая описывает явления уравнениями квантовой механики. Что же касается гравитационного поля, то управляющие им уравнения Эйнштейна - классические, не квантовые. Они служат лишь приближением к истинному квантовому описанию гравитации и перестают быть верными на очень малых расстояниях и при очень больших энергиях. Собственно, похожим образом обстоит дело и с уже упоминавшимся электромагнетизмом: Максвелл вывел тоже лишь классические уравнения, само понятие квантов появилось несколько десятилетий спустя. И когда в начале XX века был открыт целый ряд противоречащих максвелловской теории субатомных явлений, уравнения электромагнетизма пришлось пересмотреть.

Процедура построения квантовой теории на базе классической называется квантованием. Квантование электромагнетизма, осуществленное в конце 40-х - начале 50-х годов, выглядит как более или менее последовательный процесс, удачно избегнувший противоречий. Теории слабых и сильных взаимодействий вообще формулируются только как квантовые теории, поскольку описывают поведение элементарных частиц, где квантовые эффекты имеют определяющий характер.

С теорией же гравитации ситуация гораздо менее радостная, чем с электродинамикой. Несмотря на десятилетия попыток, последовательная квантовая теория гравитации так и не была построена - она неизбежно оказывалась внутренне противоречивой. Квантовые эффекты в теории гравитации существенны лишь на чрезвычайно малых расстояниях, порядка так называемой планковской длины (около 2x10^-33 сантиметра), и там с общей теорией относительности происходит что-то неладное. Сложность ситуации состоит в том, что теория гравитации описывает не просто физическое поле в пространстве-времени, но само пространство-время. Рецепт же исправления теории (не выходя за рамки теории поля) нам неизвестен, хотя пробовались всевозможные средства. Здесь на сцене и появляются струны.

Струны

Спрямляя извивы исторического развития, перейдем прямо к описанию сути «струнной идеи». К недостаткам такого подхода можно отнести отсутствие мотивировок и «вывода» теории струн из более традиционных представлений. Однако современная теория струн достаточно фундаментальна, чтобы можно было обойтись без подобных мотивировок. Все же, говоря о том, почему именно теория струн, а не теория частиц и полей оказывается правильной, стоит помнить о том, что построить последовательную теорию гравитации в традиционных рамках теории поля невозможно. Хотя сама по себе теория струн не имеет прямых экспериментальных подтверждений, ее фундаментальный характер определяется тем, что, после многих других попыток, она одна оставляет возможность включить все известные взаимодействия в единую непротиворечивую теорию. При этом теория струн предлагает единую фундаментальную сущность взамен многих; из нее можно, в принципе, вывести все свойства нашего мира, а может быть, и узнать кое о чем за его пределами.

Вместо точечных объектов, частиц, эта теория оперирует с протяженными объектами - струнами. Струну действительно можно представлять себе именно как струну, то есть как бесконечно тонкую нить, которая может сворачиваться, изгибаться и колебаться. При этом сама струна ни из чего не состоит, то есть представляет собой фундаментальный объект. Струны бывают открытыми, когда у нитки есть два свободных конца, и замкнутыми, когда оба ее конца соединены.

Колебания струн, как и колебания рояльной струны, могут происходить с разными частотами (гармониками), начиная с некоторой низшей, основной частоты. Из-за этого струны умеют делать гораздо больше разных вещей, чем частицы.

Фундаментальное значение имеет то, что на достаточном расстоянии от струны ее колебания воспринимаются как частицы. Струна, колеблющаяся с некоторой комбинацией основных гармоник, порождает целый набор частиц, причем с различным спином. Пока мы не разглядываем струну вблизи, эти частицы выглядят в точности как кванты хорошо известных полей, включая гравитационное и электромагнитное. (Напомним, что в правильной - квантовой - картине частицы уже не просто кусочки вещества, а определенные состояния более общей сущности - поля.) Масса этих частиц-полей возрастает по мере увеличения частоты породивших их колебаний струны, причем все частицы-поля, кроме нескольких, имеют огромную массу.

Обычная струна, колеблясь в воздухе, порож­дает звук. На большом расстоянии от источ­ника невозможно сказать, что породило зву­ковую волну: струна или, например, колебание столба воздуха в свистке. С точки зрения квантовой механики любая волна одновременно еще и частица. Звуковую волну можно рассматривать как поток кван­тов звука-фононов, подобных фотонам, кван­там электромагнитного излучения. Колебания фундаментальных струн тоже квантованы: на некотором расстоянии от струны ее колебание воспринимается как выб­рошенная струной элементарная частица. Однако по самой частице тоже нельзя сказать ничего определенного о породившем ее источни­ке.

В квантовой механике существенную роль играет так называемый принцип неопределенности. Согласно этому принципу любая попытка локализовать частицу в пределах очень малой длины сообщает этой частице очень большой импульс (количество движения). Разделив величину импульса на универсальную постоянную - скорость света, мы получим характерное значение массы. Таким образом, очень малая планковская длина соответствует очень большой массе, называемой планковской массой. Она превышает массу протона в 10¹⁹ раз. И частицы-поля высших гармоник колебаний струны имеют массу не меньше планковской.

Итак, струны, в силу своей врожденной способности колебаться с разными частотами, служат источниками пространственно-временных (то есть меняющихся во времени и в пространстве) полей. Поля, которые соответствуют низшей частоте, с точки зрения наблюдателя в пространстве-времени массы не имеют, а остальные поля (их бесконечно много, как и высших гармоник струны) оказываются, наоборот, очень массивными, «тяжелыми», гораздо тяжелее любой известной частицы. Для появления таких сверхтяжелых - порядка массы Планка и выше - частиц требуется энергия, которую частицы могли иметь лишь в самые ранние моменты жизни Вселенной, когда она была очень горячей.

Среди безмассовых частиц, соответствующих самым низкочастотным колебаниям струны, имеется и квант гравитационного поля - гравитон. Тем самым струны описывают именно квантовую гравитацию, ту самую теорию, построение которой традиционными средствами не представляется возможным.

Частица, двигаясь в пространстве-времени, вычерчивает линию. Струна при движении «рисует» некую, порой довольно причудливую поверхность, называемую «мировым листом».

Картина примерно такова: струны имеют очень малый характерный размер, как раз порядка планковской длины, и только в этом масштабе собственно струнные эффекты начинают играть заметную роль. На достаточном же удалении от струны наблюдатель увидит только поля (например, гравитационное и электромагнитное), кванты которых и есть колебания струны. На таких относительно больших расстояниях квантование теории Эйнштейна, то есть описание гравитации в терминах квантованного поля, оказывается вполне удовлетворительным. Но по мере приближения к планковской длине квантовое обобщение теории гравитации Эйнштейна - общей теории относительности - делается внутренне противоречивым. Однако теперь мы понимаем, что описание в терминах гравитонов перестает быть правильным само по себе: приблизиться к струне, по принципу неопределенности, означает вступить с ней во взаимодействие, то есть дернуть за струну достаточно сильно. При этом она больше не будет выглядеть как точечный объект, и потребуется честный анализ поведения струны как целого, а не просто нескольких ее гармоник. Таким образом, струнная идея исправляет квантовую теорию Эйнштейна как раз там, где она требовала какого-то вмешательства.

Как уже говорилось, теория Эйнштейна описывает не просто поле в пространстве-времени, но, в силу специфических свойств гравитации, также и само пространство-время. Так, например, в зависимости от того, насколько сильно среднее гравитационное поле во Вселенной, наша Вселенная может быть открыта или замкнута. Коль скоро теория струн «содержит» теорию гравитации, струны также способны определять характер того пространства-времени, где они распространяются. Это обстоятельство окажется очень существенным, когда мы будем обсуждать теории Калуцы - Клейна.

Предстоит еще, правда, выяснить: непротиворечиво ли в свою очередь само струнное описание? Другими словами, оказывается ли струнное исправление теории гравитации Эйнштейна математически последовательным?

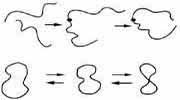При взаимодействии открытые струнымогут соединяться своими концами, а замкнутые - «лопаться», сливаться и взаимодействовать с открытыми струнами.

Ответ на этот вопрос не лишен изящества: теорию струны нужно строить весьма специальным способом, и только тогда удается получить последовательную и непротиворечивую теорию. Мы снова встречаемся здесь с общей ситуацией, которую можно охарактеризовать так: природа не терпит произвола. Правильная универсальная теория весьма строго определена (а в окончательном варианте вообще единственна), и все элементы произвола должны исключаться по мере разработки теории. Правильная теория как бы сама знает про себя все и полностью определяет, в частности, условия для своего существования.

Рисуя мировой лист, описывающий эволюцию замкнутой струны, можно получить фигуру, именуемую «штанами» (pants). При этом ука­зать точно, когда струна разделилась на две, невозможно. Наблюдатели в разных системах отсчета увидят, что это произошло в разные моменты времени t1 и t2. Из-за этой «размытости» взаимодействия струны избавлены от многих противоречий, содержащихся в теории частиц - объектов точечных.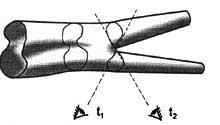

Какие же основные параметры, ничем, на первый взгляд, не регламентированные, в действительности определяются из требования непротиворечивости теории струн? Имеется последовательность все более тонких условий, применение которых в конце концов радикально сужает возможный выбор непротиворечивой теории. Эти условия мы сейчас и обсудим.

Из «штанов» собираются более сложные дву­мерные поверхности. Закрыв вырезанный кусок мирового листа «шапкой», можно из двух «шта­нов» построить тор, «крендель» и многие дру­гие фигуры. Существует математическая теорема, гласящая, что любую двумерную по­верхность можно построить, соединив друг с другом несколько «штанов».

Высокомерные струны

К парадоксальным свойствам теории струн относится то, что их квантовое описание довольно быстро приходит к внутреннему противоречию, если только размерность пространства-времени не равна 26. То есть, теория струн справедлива для какого-то мира, где есть 26 независимых осей пространства и времени. Этот несколько обескураживающий факт, казалось бы, делает теорию полностью нефизичной, отводя ей роль математически элегантной, но совершенно абстрактной модели, скорее из разряда курьезов. Мы ведь несомненно живем в четырехмерном пространстве-времени, в котором есть только три пространственных и одно временное измерение, и решительно не в состоянии увидеть ничего похожего на 26-мерный мир!

Вспомним, однако, что наши наблюдения, включая и те, которые осуществляются с помощью гигантских современных ускорителей, относятся к масштабам длин, намного превосходящим типичный струнный размер, то есть планковскую длину. Вот если бы с помощью сверхгигантского ускорителя мы могли смоделировать очень ранние моменты жизни Вселенной, то тогда ускоренные до фантастической энергии частицы вдруг почувствовали бы эти лишние измерения и могли бы «проскользнуть» в них. Масса ускоренных частиц, возрастающая из-за скорости, как раз достигла бы тогда планковской массы - примерно массы «тяжелых», наиболее высокочастотных гармоник струны. А это как раз и означало бы, что мы должны рассматривать струну как целое, а не только ее первые, «легкие», гармоники.

Некоторые неприятности, приводящие к ма­тематической непоследовательности теории струн, связаны с наличием так называемых «головастиков» - поверхностей с очень длин­ной и тонкой «шеей». Роль суперсимметрии со­стоит, в частности, в том, чтобы запретить появление наиболее противных головастиков.

И все же, если лишние измерения существуют, нельзя ли хоть как-то убедиться в их присутствии? Коль скоро при доступных нам энергиях мы не можем непосредственно заглянуть в скрытые измерения, следует внимательно оглядеть наблюдаемый мир в поисках следов, оставленных скрытыми измерениями. Такие следы действительно есть, и речь о них пойдет ниже, а пока продолжим знакомство со струной. Забегая немного вперед, скажем, что это еще не суперструна, обещанная в заглавии, а более простая, так называемая бозонная струна.

При распространении в пространстве-времени (пока, как требует теория, - в двадцатишестимерном) струна, объект одномерный, рисует некую поверхность, называемую мировой поверхностью, или мировым листом (аналогично тому, как частица - нуль-мерный объект - вычерчивает мировую линию). Мировой лист замкнутой струны может быть или сферой, или тором, или более замысловатой поверхностью типа кренделя. Для определенного вида струн имеются и более экзотические возможности, например бутылка Клейна - неориентируемая замкнутая поверхность, в определенном смысле аналог листа Мебиуса.

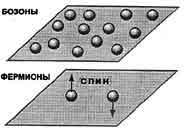Элементарные частицы по своим физическим делятся на две группы - бозоны и фермионы. К бозонам относятся фотоны, некоторые, например Не-4, молекулы газов. Бозоны неразличимы, они проявляют склонность собираться вместе без ограничения числа частиц. В группу фермионов входят, в частности, нейтроны и протоны; электроны, нейтрино и другие частицы, именуемые лептонами. Все они подчиняются фундаментальному принципу Паули, который запрещает двум фермионам находиться в одном, и том же состоянии.

Двумерная поверхность мирового листа сама по себе служит ареной, на которой нечто может происходить. На ней, в частности, могут жить двумерные, непосредственно не наблюдаемые, поля. Для них мировой лист струны будет своей Вселенной. Свойства струны в сильной степени зависят от того, какие именно поля поселены на ее мировом листе. Точнее, пока сама струна обитает в двадцати-шестимерии, на ее мировом листе ничего не живет и мы имеем именно «наивную», голую струну. Но если на мировой поверхности струны поселить некоторые новые поля, может оказаться, что струна «научится» жить и в пространстве меньшей размерности. Степени свободы этих новых двумерных полей в определенном смысле играют роль недостающих пространственных размерностей и тем самым эффективно восстанавливают 26-мерие.

Но условия непротиворечивости теории струн не ограничиваются предоставлением струне 26-мерного пространства или вселением дополнительных двумерных «существ» на ее мировой лист. Как уже упоминалось, различные гармоники колеблющейся струны воспринимаются наблюдателем как частицы, и низшие гармоники должны соответствовать безмассовым частицам. Однако с бозонной струной случилась весьма неприятная история: первая, самая низкочастотная ее гармоника воспринимается в пространстве-времени как частица мнимой массы. Такие гипотетические частицы называют тахионами; они имеют дурную славу за то, что им полагается двигаться со скоростью больше скорости света. Появление таких частиц в математическом аппарате конкретной физической системы, в данном случае струны, означает ее нестабильность: тахионы немедленно забирают из системы всю энергию и улетают неизвестно куда. Тахионы сигнализируют, что состояние системы, в котором они могут возникнуть, нестабильно и распадается на какие-то состояния, лишенные тахионов.

Теория самых простых, бозонных, струн, таким образом, оказывается нестабильной и, значит, должна перестраиваться в более устойчивые образования. И действительно, существует вариант теории струн, свободный от тахионной нестабильности. Такие струны основаны на суперсимметрии, к которой мы сейчас и переходим.

Электроны, будучи фермионами, подчиняют­ся принципу Паули и «не имеют права» нахо­диться на одной орбите в одном и том лее со­стоянии. Они распределяются по разным орби­там, и число электронов на самой верхней ор­бите атома элемента определяет его химичес­кие свойства. Если бы электроны были бозона­ми, то во всех атомах они сидели бы вместе на самой нижней орбите и химические свойства элементов были бы одинаковыми.

Бозоны, фермионы и суперсимметрия

Все «элементарные» частицы делятся на два класса - бозоны и фермионы, которые радикально отличаются по своим свойствам. Бозоны могут собираться вместе, буквально сидя друг на друге, а каждый фермион непременно должен быть единственной среди себе подобных частиц, находящихся в данном состоянии. К бозонам принадлежат, например, фотон и гравитон, а к фермионам - электрон. Различия в физическом поведении двух классов частиц требуют для своего количественного описания определенного расширения традиционной математики. Переменные, с которыми оперирует «обычная» математика (например, координата частицы), могут принимать обычные числовые значения, что и определяет правила (обычные!) действия с этими переменными. Но последовательное описание фермионов требует введения новых переменных. Фермионные переменные не могут принимать никаких числовых значений, кроме нуля, но при этом не равны нулю (!) и обладают еще одним парадоксальным свойством: при перестановке двух фермионных сомножителей их произведение меняет знак. Таким образом, произведение зависит от порядка следования сомножителей. Обычные же, не фермионные переменные называются бозонными. Каждый тип переменных нужен для описания соответствующих частиц и полей.

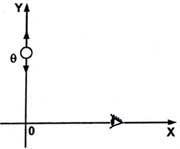Фермионные переменные Q - важный и совершенно непривычный для нас элемент теории струн. Эти переменные не числа, они могут принимать только нулевые значения. Неточ­ной аналогией этому свойству может слу­жить система координат, в которой числовую ось х пересекает ось фермионных переменных у. Фермионные переменные могут принимать любые значения, но наблюдатель, «живущий» на оси х, будет видеть переменную Q только в точке 0. Отличие фермионных переменных от бозонных заключается в том, что в известном смысле их ось бесконечно коротка, но неравна при этом нулю. С фермионными переменными молено произво­дить далеко не все математические операции, применимые к обычным числам. Их можно, например, перемножать, но делить на них нельзя. Поэтому из равенства Q-Q - 0, справед­ливого для всякой фермионной переменной, не следует, что Q = 0. Наше четырехмерное пространство-время - только тонкая «кожа» на поверхности некоторого двенадцатимерного многообразия, в котором живет М-теория. Гравюра голландского художника М. Эшера «Лента единства».

Фермионы и бозоны могут сосуществовать в одной и той же физической системе. Может случиться при этом, что такая система будет обладать особым видом симметрии - так называемой суперсимметрией, отображающей бозоны в фермионы и наоборот. Для этого, конечно, требуется равное количество бозонов и фермионов, но условия существования суперсимметрии этим не ограничиваются. Проверить наличие суперсимметрии в данной системе бывает очень непросто, и вообще, описание суперсимметричных систем в терминах обычного пространства-времени - дело нелегкое. Это происходит потому, что суперсимметричные системы на самом деле живут в суперпространстве. Суперпространство получается из обычного пространства-времени, когда к нему добавляются фермионные координаты. В суперпространственной формулировке преобразования суперсимметрии выглядят похожими на вращения и сдвиги в обычном пространстве. А живущие в нем частицы и поля представляются набором частиц или полей в обычном пространстве, причем таким набором, в котором строго фиксировано количественное соотношение бозонов и фермионов, равно как и некоторые их характеристики (в первую очередь спины). Входящие в такой набор частицы-поля называются суперпартнерами.

Суперпространства, несмотря на целый ряд необычных свойств (или скорее благодаря им), обладают интересной геометрией. Геометрические свойства суперпространств таковы, что живущие в них квантовые теории не могут слишком многого себе позволить, и, как следствие, ряд проблем, возникающих при квантовании чисто бозонных или чисто фермионных теорий, не возникают в суперпространстве. А если и возникают, то носят гораздо более контролируемый характер. Это происходит оттого, что суперпартнеры «кооперируются» и замечательным образом сглаживают «недостатки» друг Друга.

Именно суперсимметрия приходит на выручку бозонной струне, пораженной нестабильностью. Суперсимметричная струна обладает рядом уникальных свойств, которые делают ее мостом к наиболее фундаментальному описанию как нашего Мира, так и, возможно, неких других миров за его пределами.

Суперструны

Именно суперсимметрия приходит на выручку бозонной струне, пораженной нестабильностью. Этой нестабильности не возникает при квантовании суперструны.

Суперструна - это суперсимметричная струна, то есть по-прежнему струна, но живущая не в обычном нашем пространстве, а в суперпространстве. Или, что в конечном итоге оказывается эквивалентным, хотя и не очевидным заранее, это струна в обычном (бозонном) пространстве, на мировом листе которой живет определенный набор фермионных полей и имеется суперсимметрия. В любой формулировке суперсимметрия накладывает весьма жесткие ограничения на квантовое поведение суперструн. Она влияет также и на то, в пространстве какой размерности струна, в данном случае суперструн, избавлена от противоречий. Такой размерностью оказывается 10 - несколько ближе к желанным четырем, чем 26, но все же достаточно далеко. Будет нелишним подчеркнуть, что фермионы населяют мировой лист суперструны уже в выделенной размерности 10, и именно их присутствие делает струну суперсимметричной.

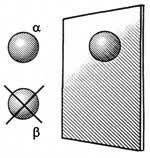
В суперсимметричных теориях каждая части­ца обязана иметь супсрпартнера. Суперпарт­нер частицы а- частица совсем другого типа (не античастица!), но она обязана принимать участие вместе с а во всех процессах, с нею про­исходящих. Теория будет непротиворечивой, только если ни при каких условиях не сможет родиться частица без суперпартнера. Появле­ние таких одиноких частиц означало бы нару­шение суперсимметрии

Что же касается тахиона, то он просто не может возникнуть в суперструне, поскольку его появление противоречило бы суперсимметрии (у него не может быть суперпартнера). Тем самым суперсимметрия исправляет весьма вредный недостаток бозонной струны. Более того - она приводит к новым условиям внутренней самосогласованности. Теория будет последовательной лишь тогда, когда, что бы ни происходило, суперсимметрия сохранится. Это значит, что в ней не появятся объекты без суперпартнеров. Другие симметрии, имеющиеся в теории, также должны сохраняться при квантовании. Это, однако, не всегда легко получается, если имеются фер-мионы определенного вида, реализующие суперсимметрию. Поэтому, начав с классической теории, далеко не всегда можно построить последовательную квантовую теорию. Как уже говорилось, это означает, что Природа описывается не какой попало теорией, а только той, видимо единственной, которая на всех уровнях свободна от противоречий.

В терминах частиц-полей в десятимерном пространстве-времени, на достаточном удалении от суперструны возникает прежде всего суперсимметричный вариант теории гравитации называемый, конечно, супергравитацией. Теории супергравитации стали прекрасным примером того, сколь сильно суперсимметрия чувствительна к размерности пространства-времени. Оказалось, что никакие супергравитации невозможны в размерности больше 11, тогда как в размерностях от 2 до 11 им жить хорошо. Десятимерные теории супергравитации как раз и представляют собой определенный предел, к которому сводится теория суперструн на больших расстояниях, а супергравитации в более низких размерностях получаются из десятимерных. Таким образом, в известном смысле ничего нового по сравнению с суперструнами не обнаружено. Независимо сформулированные теории поля в действительности оказались лишь пределом теории струн, а их симметрии - некоторой частью симметрии струнных теорий.

Впрочем, это было бы в точности так, если бы не одна-единственная теория одиннадцатимерной супергравитации - она не следует ни из какой теории суперструн, потому что струны не могут жить в размерности больше десяти. До самого последнего времени одиннадцатимерная супергравитация оставалась раздражающим фактором: будучи, в общем, похожа на тесно связанные с суперструнами теории полей-частиц, она сама ни с какой суперструной связана быть не может, из-за чего выглядит не-необходимой и потому не вполне понятной.

В суперструну можно встроить еще некоторую дополнительную симметрию, и тогда в пределе больших расстояний наряду с супергравитацией возникает еще так называемая теория Янга - Миллса. Она похожа на те, что описывают поведение кварков и глю-онов, но только в десяти измерениях и в суперсимметричном варианте. Размер и тип янг-миллсовской симметрии может быть выбран, казалось бы, произвольно, а потому число различных десятимерных струнных теорий должно быть бесконечно. Но свободными от противоречий оказываются лишь пять вариантов теории десятимерных суперструн! Таким образом, условия существования симметрии на уровне струн - более фундаментальном, чем уровень полей-частиц, - накладывают существенно более сильные ограничения. Говоря о струнах, мы теперь всегда будем иметь в виду именно суперструну в одном из непротиворечивых вариантов этой теории.

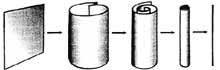
Скрутив плоский лист бумаги (желательно представить его бесконечным) в достаточно тонкую трубку, мы, «убиваем» одно измерение: на большом расстоянии она представляется лини­ей - одномерным объектом, а не двумерным, ка­ким была плоскость. Аналогичным образом мож­но «скрутить» пространство любого числа изме­рений, понизив его размерность. Понятно, что по мере роста числа размерностей простран­ства значительно возрастает число способов, которыми можно осуществить подобное скручи­вание, хотя наглядно представить себе (и тем более нарисовать) это невозможно.

Конечно, столь сильное сокращение произвола в построении теории - от бесконечности до пяти - результат весьма впечатляющий, и говорит он о том, что в поисках единой «теории всего» мы на правильном пути. И тем не менее пять - это слишком много, когда речь идет о действительно единой теории. Некоторое время казалось, что «было бы гораздо лучше», если бы требования математической состоятельности выделяли вместо пяти одну теорию. Но недавно события приняли непредвиденный оборот, да так, что заодно исчез и раздражающий фактор одиннадцатимерной супергравитации. Но прежде, чем рассказывать об этом, нам необходимо разобраться с тем, как же «привязать» хотя бы одну из пяти десятимерных теорий к нашему четырехмерному миру.

Калуца - Клейн и четырехмерная физика из суперструн

Каково же взаимоотношение четырехмерной физики и теории струн, скажем, в десятимерном пространстве-времени? Понимание того, как «скрытые» измерения влияют на четырехмерный мир, - одно из важнейших достижений современной теоретической физики. Но сама по себе идея взаимного влияния пространств разной размерности, называемая по имени впервые предложивших ее ученых теорией Калуцы - Клейна, была высказана сравнительно давно. Речь здесь идет вот о чем.

Начнем с простейшего случая и постараемся понять, каким образом пятимерный мир можно привести к четырехмерному. Для этого в пятимерии нужно рассматривать не плоское пространство, а пространство, превращенное в этакий цилиндр, то есть считать одно из измерений свернутым в кольцо. Скрутив в тонкую трубку лист бумаги, можно подумать, что перед вами не плоскость, каковой был этот лист, а линия, одномерное пространство. Конечно, посмотрев повнимательнее, вы увидите, что это вовсе не линия, а именно трубка.

Но теперь представим себе, что по листу бумаги бегают какие-то частицы. Пока лист не скручен или пока радиус скрученного листа не слишком мал, эти частицы бегают во всех направлениях. По мере того, как уменьшается радиус цилиндра, частица обегает вокруг трубки все быстрее и быстрее. В то же время движение вдоль трубки происходит по прямой, точно так же, как и раньше, на плоском листе. А теперь предположим, что обход по окружности занимает очень мало времени, и мы просто не в состоянии заметить, что частица двигалась в этом направлении: нам кажется, что она может двигаться только вдоль «плоского» направления, вдоль трубки. Таким образом, мы свели двумерное пространство к одномерному!

В действительности движение по измерениям, закрученным в кольцо, не удается заметить по весьма фундаментальной причине - согласно принципу неопределенности. Чем меньше размеры, в которые надо втиснуть частицу, тем большая энергия для этого требуется. Таким образом, как только лишние измерения сворачиваются в достаточно маленькие окружности, у нас просто не хватит энергии, чтобы заставить какую бы то ни было частицу бежать по этой окружности, так что это измерение как бы исчезает.

Вспомним теперь, что частицы в микромире - это кванты соответствующих полей и что последовательное описание взаимодействий в природе достигается именно на языке полей. Поля могут иметь несколько (иногда - до нескольких сотен) различных компонент, и, как правило, их тем больше, чем больше размерность пространства-времени. Компоненты - это как бы отдельные поля, но они собраны в единую структуру и без нее не обладают полной самостоятельностью. Например, электромагнитное поле в четырехмерном пространстве-времени имеет четыре компоненты, две из которых по некоторым причинам ненаблюдаемы (они «нефизические»), а две другие соответствуют двум направлениям поляризации фотона. Теперь представим себе, что поле живет в пространстве, одно или несколько измерений которого свернуты в маленькие окружности, так что получается эффективное пространство меньшей размерности. В этом случае полю требуется преобразовать себя таким образом, чтобы число компонент уменьшилось до количества, которое и ожидается от него в пространстве меньшей размерности. Лишние компоненты поля при этом оказываются полностью независимыми и выступают как новые поля.

Идея подхода Калуцы - Клейна, таким образом, состоит в том, что некоторые наборы вроде бы никак не связанных полей в четырехмерном пространстве-времени могут оказаться осколками единого поля в пространстве более высокой размерности. Если дело обстоит именно так, то мы получаем уникальный механизм построения единой теории поля, то есть именно единой теории, описывающей различные поля. Истинной же ареной для этой единой теории служит пространство более высокой размерности. Десятимерие и одиннадцатимерие для этого прекрасно подходят. Во-первых, у живущих там полей достаточно компонент, чтобы упаковать в них имеющиеся четырехмерные поля. А во-вторых, в десятимерии (или одиннадцатимерии) еще существует суперсимметрия, которая в том или ином виде перейдет по наследству в четырехмерие, определив ряд его хороших свойств. «Максимальные» супергравитации живут как раз в размерностях 10 и 11 и, раскалываясь на куски при свертывании ряда измерений, «выпадают» в довольно замысловатые теории, включающие супергравитации в низших размерностях.

Струна способна наматываться на такие скрученные пространства, которые имеют внутри некоторое подобие дырок (в простей­шем случае это тор), и поэтому не может с них соскочить. А со сферы, например, любая замк­нутая струна может сняться, стянувшись в точку. Намотанные таким образом струны порождают колебания, отличные от колеба­ний свободных струн.

Но как только выбор «большой» теории сделан, немедленно возникает следующий вопрос: можно ли объяснить, почему, скажем, десятимерная теория предпочла расколоться на 4 + 6 измерений, а не, скажем, на 5 + 5 (тогда мы жили бы в пятимерном пространстве-времени, а свернутыми в колечки были бы еще пять измерений). В действительности, как мы видим, свернутых измерений должно быть шесть, что оставляет нам только четыре несвернутых.

Более того, лишние измерения не обязательно должны сворачиваться именно в окружности. Когда перед нами стоит задача «скрутить» два измерения, то скручивание их в окружности дает тор. Но ничем не хуже будет и другое замкнутое двумерное пространство - сфера. По мере того, как число измерений растет, обнаруживается все больше способов выбрать такие замкнутые пространства.

Какое именно пространство и какой размерности реализуется? Это зависит от того, как развивается система во времени в соответствии с ее внутренним законам. Так же, например, как динамика атмосферных потоков определяет погоду и стабильно (по крайней мере, в течение последних 5000 лет) засушливый климат Сахары. А серьезные изменения, скажем, в структуре океанских течений могут привести к изменению климата. К счастью для нас, конфигурация пространства-времени, установившаяся в течение последних 15 миллиардов лет, несколько более стабильна, чем погода. Только на очень ранних этапах жизни Вселенной количество скрученных измерений могло меняться. Например, рожденный десятимерным мир мог вскоре предпочесть шесть свернутых измерений, оставив для нас ставшие уже привычными четыре.

Нам пока неизвестно, как именно осуществляется выбор между различными структурами «свернутых» пространств и тем самым между различными размерностями и свойствами четырехмерного пространства- времени. Но мы знаем, что такая возможность выбора встроена в теорию суперструн, поскольку струны порождают гравитацию, которая и определяет геометрию пространства-времени. И мы также в состоянии определить, может ли, в принципе, то или иное шестимерное пространство быть отобрано суперструной для того, чтобы из десятимерия получился наблюдаемый четырехмерный мир. Определяющим критерием здесь служит суперсимметрия: не во всяком пространстве может жить суперструна. Кроме того, структура шестимерного пространства должна быть согласована с наблюдаемыми свойствами нашего мира.

Дело в том, что при скручивании лишних измерений в очень маленькие пространства свойства теории в остающихся измерениях отражают некоторые геометрические характеристики этих пространств. Так, например, число поколений элементарных частиц связано с характеристиками, примерно описывающими количество «дыр» в пространстве свернутых измерений. Поэтому не полностью пока известная нам теория строится как бы с двух сторон. От наблюдаемых при доступных нам малых энергиях свойств элементарных частиц переходят к теории струн, пытаясь эти свойства экстраполировать на очень высокие энергии, существенные для струнного описания. А в рамках собственно струнной формулировки стараются увидеть, каковы механизмы, «переводящие» струнные сущности (иногда непосредственно не наблюдаемые, вроде свойств обитателей мирового листа струны) в термины геометрии скрученных измерений, а оттуда - на язык четырехмерного пространства-времени и живущих в нем элементарных частиц. Полученная этим путем теория должна объяснить, почему суперструны выбирают именно наш четырехмерный мир, предпочтя его другим возможностям (например, шестимерное или четырехмерное, но в каком-нибудь смысле «перекошенное», пространство-время, или вообще нечто иное вместо пространства-времени). Часть из встречающихся на этом пути сложностей обсуждается ниже.

Теория возмущений

Часто упоминаемые «технические» сложности теоретической физики в значительной мере обусловлены следующим обстоятельством. По какой-то причине, обсуждать которую мы не можем, физические процессы описываются уравнениями, как правило, с заданными начальными или иными условиями. Например, измерив координаты и скорости всех тел в Солнечной системе на 1 января 1900 года, мы можем, в принципе, решить соответствующие уравнения и, таким образом, найти их положения в любой момент времени. Однако реально сделать это можно лишь в некотором приближении, иначе уравнения просто невозможно решить. Это обстоятельство вовсе не означает вселенской катастрофы, но содержит массу неудобств: решение существует, но у нас, например, нет возможности записать его на бумаге. Приближение, в котором мы все-таки можем кое-что (иногда не так уж и мало) сделать, состоит в том, чтобы считать Солнце неизмеримо тяжелее всех планет. Это приближение почти работает, в особенности для легких планет, но для тяжелых оно уже вступает в серьезное противоречие с результатами точных наблюдений. Юпитер, Сатурн, Уран и Нептун все-таки достаточно массивны, и существование каждого из них отражается на соседях. Чтобы уточнить движение, скажем, Урана, можно считать, что его тяжелые соседи движутся по своим независимым траекториям и оттуда воздействуют на Уран. В действительности, скажем, Юпитер в свою очередь подвергается притяжению Сатурна, Урана, Нептуна, и на самом деле его траектория более сложная. Но для расчета малых возмущений интересующего нас Урана такие детали в поведении Юпитера не важны. Подобный подход известен как теория возмущений. Названа она так потому, что сначала делают упрощенные предположения и находят невозмущенное движение каждого тела, а потом вычисляют поправки - возмущения этого движения.

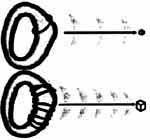
Колебания свободной струны могут происхо­дить с различными частотами. На достаточ­ном удалении эти колебания выглядят как ча­стицы, масса которых тем больше, чем выше частота колебаний струны.	Струны, намотанные на скрученные про­странства, на достаточном расстоянии тоже «выглядят» как частицы. Масса этих частиц определяется числом витков намотанной струны. Но эти частицы будут отличаться от частиц, соответствующих колебаниям струны ненамотанной.

Теория возмущений может быть корректной только когда одни эффекты (притяжение планет между собой) малы по сравнению с другими (притяжением планет к Солнцу). А вот в интересной задаче тройных звезд - когда все три тела сравнимы друг с другом по массе - теория возмущений совершенно неприменима, развить подобную схему вычислений просто невозможно. Подобная ситуация описывается термином «сильная связь» (или сильное взаимодействие). Задачи с сильным взаимодействием надо решать точно, а не по теории возмущений, но это удается лишь в исключительных случаях.

Струны за пределами теории возмущений

Ситуация в теории струн не менее драматична. Все дело в том, какие новые возможности открываются в теории струн, по сравнению с теорией полей-частиц, при использовании механизма Калуцы - Клейна. Струны могут делать нечто, совершенно недоступное частицам: при наличии хотя бы одного скрученного измерения они могут наматываться на маленькое колечко, соответствующее этому измерению. Струна может обкрутиться вокруг такого кольца один или несколько раз. А с точки зрения наблюдателя в пространстве-времени, как ни странно, такое поведение струн будет приблизительно описываться как появление некоторых частиц. При определенных соотношениях между радиусом свернутого измерения и интенсивностью взаимодействия струн такие частицы становятся легкими, и имеет смысл сравнивать их с теми безмассовыми частицами, которые ожидались с самого начала, - они соответствуют низшим гармоникам колебаний струны.

В итоге получается, что при слабом взаимодействии между струнами, в области применимости стандартной теории возмущений, струна рождает частицы определенного типа, реализующие определенные симметрии в частности - суперсимметрию. В другом диапазоне интенсивности взаимодействия струн, уже вне рамок обычной теории возмущений, струна может порождать совсем другие частицы с другими симметриями и суперсимметриями. Что же такое струна «на самом деле»? Какие частицы в ней все-таки есть, а каких нет?

Вопрос стоит даже еще более серьезно, поскольку дело не ограничивается только частицами.

Теория каждого из пяти типов суперструн способна таким (или почти таким) способом порождать наборы новых частиц, которые выглядят соответствующими колебаниям суперструны другого типа. Это происходит вне рамок теории возмущений, в области сильной связи. Так, теория, имеющая в области слабой связи тип I, умеет где-то в области сильной связи «притворяться» теорией типа II, и наоборот. Но тогда приходится признать: все, что мы думаем о теории струн в области ее слабой связи, своего рода «притворство», то есть описание только части полной теории. Полная же теория имеет различные «секторы», в которых она приближенно описывается разными типами теории струн. Но тогда она сама по себе не может быть только теорией струн.

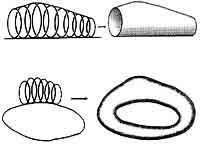
Располагая над каждой точкой одномерного пространства - линии - кольца и сливая их вместе, мы получим двумерное пространство - цилиндр. Проделав такую же процедуру с замкнутой линией, мы построим тор. Анало­гичным образом с каждой точкой нашего четы­рехмерного пространства-времени ассоцииро­вано шестимерное пространство. Вместе они образуют десятимерное пространство.

Само описание теории струн как таковой оказывается лишь приближением к какой-то фундаментальной теории, для описания которой у нас нет пока адекватного языка. Настоящая теория только выглядит как теория струн в области своей слабой связи и в некоторых диапазонах области сильной связи. А об устройстве области сильной связи в целом мы только начинаем догадываться.

Конечно, чрезвычайно хочется узнать: а как же на самом деле выглядит теория, впервые приоткрывшаяся нам в форме теории суперструн? На выяснение этого интригующего вопроса в последнее время направлено множество усилий. Уникальна сама по себе возможность - впервые(!) - всерьез обсуждать подобные вопросы. Искомая теория получила название М-теории, от слова mystery (тайна, загадка) или от слова мембрана (почему, будет вкратце объяснено ниже). Это именно та теория, различные фазы которой может приближенно описывать одна из пяти имеющихся в десятимерии теорий суперструн. Вспомним, например, что обычная классическая ньютоновская механика оказывается приближенным описанием релятивистской механики Эйнштейна. И та же классическая механика - приближение, но уже в другой области, к квантовой механике.

М-теории удается «выпадать» в каждую из теорий суперструн только если она - М-теория - живет в пространстве размерностью более десяти. Первоначально предлагалось поселить эту теорию в одиннадцатимерии. Тогда, используя механизм Калуцы - Клейна, можно примерно увидеть, каким образом «лишние» (по сравнению с десятимерием) степени свободы теории в одиннадцатимерном пространстве комбинируются в десятимерный мир, населенный суперструнами. Одна из теорий суперструн получается, когда одиннадцатое измерение скручивается в очень маленькую окружность. Другой ее вариант возникает, когда М-теория выделяет два десятимерных подпространства в одиннадцатимерном пространстве - две параллельные гиперплоскости на некотором, опять же очень малом, расстоянии друг от друга. Тогда 10-мерный мир воспроизводится граничными эффектами чего-то более общего, происходящего во всем объеме 11-мерного пространства.

Ряд тонких свойств каждой из пяти суперструнных теорий, до этого казавшихся удивительной игрой случайностей, приобретают теперь прозрачное объяснение. В соответствии с современной теоретической физикой это должно означать, что М-теория действительно существует, хотя мы знаем только о ее поведении при специальном скручивании и других сходных действиях в одиннадцатом измерении. Впрочем, есть и еще один ключ: в пределе, при слабой связи и низкой энергии, М-теория превращается в одиннадцатимерную супергравитацию. Таким образом, заодно оказалось, что высшая суперсимметричная теория поля, до этого стоявшая несколько особняком от суперструн, может быть включена в единую картину Мира!

Желание вывести из единого источника все теории суперструн требует еще одного шага в сторону более высокой размерности. Требуется двенадцатимерное пространство, в котором, наряду с десятью пространственными измерениями, имеется два времени. Наличие двух временных переменных часто порождает ситуации, противоречащие интуиции, поскольку всегда считалось, что всерьез можно рассматривать максимум одно такое измерение. И действительно, нелегко представить себе, каким образом, например, назначать свидание в мире с двумя независимыми временами. И как понять, какие события произошли в прошлом (вдоль какого времени?), а какие - нет.

Загадочным в искомой двенадцатимерной теории оказывается еще следующее обстоятельство: в то время как каждая из пяти теорий суперструн суперсимметрична, никакой подобной суперсимметрии в двенадца-тимерии существовать не может (как уже упоминалось, суперсимметрия весьма чувствительна к размерности пространства, в котором ей предстоит действовать). Это бросает вызов исследователям: как сконструировать теорию, которая не суперсимметрична, но скрывает в себе способность порождать различные суперсимметричные теории в низших размерностях? Жесткие требования суперсимметрии при отборе жизнеспособных теорий должны замениться на какой-то руководящий принцип, который, не будучи суперсимметрией, действует по крайней мере столь же эффективно.

Итак, чего же ждать от М-теории? Создаваемое ею пространство-время, вместе с находящимися в нем полями, только одна из возможностей развития этой теории. Привычное нам пространство-время существует в «суперструнной» фазе М-теории, но она сама по себе кроме суперструн содержит протяженные объекты более высокой размерности. Ими могут быть, например, мембраны. Сама по себе мембрана - поверхность двумерная, а ее эволюция описывается уже трехмерным мировым объемом, в котором два пространственных и одно временное измерение. Мембраны называют еще странным термином - «2-браны», подчеркивая их двумерность. Наряду с 2-бранами могут существовать 3-,..., 10-браны, и некоторые из них (в суперсимметричном варианте) действительно можно разглядеть в М-теории. К сожалению, исследовать их очень трудно, если только это не 1-браны, то есть струны. Известно, что некоторые из них дают двойственное описание тех же самых струн, а другие двойственны друг другу, и не все из них оказались фундаментальными, «элементарными», объектами в М-теории. Похоже, что М-теория в определенных фазах способна создавать «много-браны», а в другой фазе вместо этого создавать суперструны в пространстве-времени с десятью и с меньшим числом измерений. М-теория знает, как подобные миры взаимодействуют, дробясь и сливаясь друг с другом. Динамика, в которой сосуществуют объекты разных врожденных размерностей, должна быть очень сложной, и мы пока не знаем лежащего в ее основе принципа. Удивительно же на настоящий момент уже то, что мы вообще догадались о существовании подобной теории и осмеливаемся задавать вопросы, ответы на которые не только опишут свойства нашего мира, но и позволят сделать заключение о возможности сушествования и свойствах других миров, совершенно не похожих на наш.

Заключение

Одному из ведущих исследователей теории струн принадлежит высказывание, что суперструны - это часть физики XXI века, случайно проскользнувшая в наше время. Если так, то тем больше оснований думать о том, как нам повезло. Открытые теоретиками по совершенно другому поводу, по существу действительно случайно, струны обогатили теоретическую физику рядом новых идей и концепций, предложив нам средства, позволяющие уже сейчас всерьез задумываться о строении Мира даже за пределами наблюдаемой его части.

Как представить непредставимое, или кое-что о четвертом измерении

Представить себе суперструны, живущие в пространстве десяти измерений, действительно чрезвычайно сложно. Весь наш повседневный опыт говорит, что пространство должно иметь только три измерения, и мы не в силах представить себе, каким образом, например для отображения времени, можно расположить четыре перпендикулярные друг к другу координаты, не говоря уже о десяти, одиннадцати или двенадцати.

Математикам проще. Им нет нужды думать, как будет выглядеть, скажем, многомерная сфера. Они оперируют уравнениями. Выражение x² + у² = R², например, описывает окружность на плоскости (в двумерном пространстве) с центром в начале координат. Трехмерную сферу определяет уравнение x² + у² + z² = R². В пространстве четырех измерений аналогичная формула опишет четырехмерную гиперсферу x² +y² + z² + u² = R². Добавив нужное число координат, можно получить пяти-, шести-, и вообще любую n-мерную гиперсферу: x² +у² + z² + u² + v² +.... + w² = R², не задумываясь о том, как ее можно было бы представить наглядно. Аналогичным образом математики используют уравнения для описания гораздо более сложных поверхностей (их называют уже подмножествами) в пространствах любого числа измерений и даже дробной размерности.

Передвигая отрезок длиной L по плоскости, можно «нарисовать» квадрат. Квадрат, сдвинутый в пространстве, сформирует куб. Сумев каким-то образом «вдвинуть» кубе четвертое измерение, мы получили бы гиперкуб.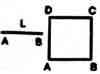
Плоское изображение трехмерного куба. Дальняя его грань уменьшена, а четыре боковые грани выглядят как трапеции из-за перспективного сокращения.
Объемное изображение четырехмерного гиперкуба. В перспективе шесть его боковых граней выглядят как усеченные пирамиды, а задняя грань кажется кубиком меньших размеров, чем передняя.

И все-таки попытаемся представить себе, как будет выглядеть в нашем трехмерном пространстве, скажем, четырехмерный куб (на большее число измерений у нас просто не хватит воображения).

В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат ABCD. Повторив эту операцию с плоскостью, получим трехмерный куб ABCDHEFG. А сдвинув куб в четвертом измерении (перпендикулярно первым трем!) на расстояние L, мы получим гиперкуб.

Одномерный отрезок АВ служит гранью двумерного квадрата ABCD, квадрат — стороной куба ABCDHEFG, который, в свою очередь, будет стороной четырехмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат — четыре вершины, куб — восемь. В четырехмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 — сдвинутого в четвертом измерении. Он имеет 32 ребра — по 12 дают начальное и конечное положения исходного куба, и еще 8 ребер «нарисуют» восемь его вершин, переместившихся в четвертое измерение.

Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и еще четыре опишут его стороны). Четырехмерный гиперкуб имеет 24 квадратные грани —12 квадратов исходного куба в двух положениях плюс 12 квадратов от двенадцати его ребер.

Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трехмерного пространства, будет выглядеть четырехмерный гиперкуб. Воспользуемся для этого уже знакомым методом аналогий.

Возьмем проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединенные четырьмя линиями — боковыми ребрами. Аналогичным образом четырехмерный гиперкуб в пространстве трех измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединенных восемью ребрами. При этом сами «ящики» — трехмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие (они нарисованы пунктиром), протянутся в четвертом измерении. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.

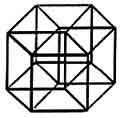	Под другим углом зрения все восемь кубических граней гиперкуба будут выглядеть несколько иначе.
	На двумерной развертке куба все шесть его граней расположатся в одной плоскости.
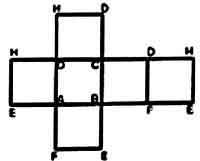
	Трехмерная развертка четырехмерного гиперкуба образует объем, составленный из восьми кубов.

Подобно тому, как трехмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвертое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Ее часть, оставшаяся в «нашем» пространстве, нарисована сплошными линиями, а то, что ушло в гиперпространство, — пунктирными. Сам же четырехмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трехмерный куб можно «нарезать» на бесконечное количество плоских квадратов.

Разрезав восемь граней трехмерного куба, можно разложить его в плоскую фигуру — развертку. Она будет иметь по квадрату с каждой стороны первой, исходной, грани плюс еще один — грань, ей противоположную. А трехмерная развертка четырехмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс еще одного — конечной «гиперграни».

Конечно, даже наглядное представление о четырехмерном гиперпространстве вряд ли поможет понять, как выглядит 10 — 12-мерие, а рассказ о суперструнах может отпугнуть своей сложностью. Но даже и в этом, самом неблагоприятном для читателя случае рассказ о суперструнах выполнил по крайней мере одну из своих задач. Он ярко показал, насколько непрост наш мир и как интересно его исследовать.

От четырехмерия — к М-теории

Современная физическая теория невероятно сложна. Чтобы хоть немного понять даже популярное ее изложение, нужно затратить массу умственных усилий, не раз и не два прочитать статью.

Совсем недавно — каких-нибудь несколько десятков лет назад — абсолютно непонятной и дикой казалась квантовая механика. Сегодня она служит рядовым инструментом физических и даже инженерных расчетов.

Но каким бы странным ни казался мир, раскрывшийся в крайне упрощенных аналогиях на цветной вкладке, следует знать, что он — не плод фантазии. За ним стоят множество серьезных исследований, очень глубокая физика и математика.

Четырехмерный мир, к которому мы привыкли, — только «тонкая кожа» на теле мира многомерного. Тот, кто мог бы посмотреть вдоль дополнительных измерений, увидел бы их свернутыми, причем иногда довольно причудливым образом, в замкнутые пространства. В этих пространствах имеется множество так называемых нестягиваемых циклов — замкнутых подпространств меньшей размерности, которые нельзя сжать в точку из-за «дырки в середине» — например, колец, охватывающих тор. В то же время кольцо, лежащее на сфере или эллипсоиде, может соскочить, поскольку оно «ни за что не зацеплено». На рисунке по понятным причинам все они показаны привязанными к отдельным точкам нашего четырехмерного пространства-времени. На самом деле с каждой его точкой связано невидимое шестимерное пространство, и при переходе от точки к точке по четырехмерию различные части этого шестимерного пространства по-разному деформируются.

ЛИБО

Как оказалось, именно количество и свойства нестягиваемых циклов в шестимерном пространстве должны определять характеристики элементарных частиц, наблюдаемых нами в четырехмерии. Поэтому-то так важно изучать геометрию подобных скрученных пространств. Уже одно только условие, что там могут существовать суперструны, выделяет определенный класс геометрий: суперструны не смогут жить в произвольно взятом n-мерном пространстве, и фундаментальные свойства нашего четырехмерия тоже не могут быть произвольными. В доступной нашему анализу области не слишком больших энергий живущие в десятимерии суперструны каждого из пяти типов сворачивают шесть лишних измерений в замкнутые пространства немного различным образом. Точнее говоря, нам удается «увидеть» только определенные части выбранных суперструнами внутренних пространств. Намотанные суперструны создают элементарные возбуждения (частицы), не похожие на те, которые создаются ненамотанными струнами. При этом в далеких «закоулках» скрученного пространства (уже, строго говоря, соответствующих области высоких энергий) можно разыскать циклы, при намотках на которые струна типа I порождает такие же возбуждения, как ненамотанная струна типа II. На самом деле каждая из пяти теорий десятимерных суперструн дает неполное описание некоторой единой теории, названной недавно М-теорией (от слова mystery — загадка, тайна). Способность суперструн различных типов порождать друг друга, наматываясь на подходящие циклы, объясняется тем, что каждая из теорий суперструн происходит из М-теории. М-теория сама по себе не сводится к теориям суперструн и живет, по-видимому, в двенадцатимерном «пространстве-времени», в котором, однако, имеется два времени.

Будем двигаться теперь по рисунку снизу вверх, от М-теории к суперструнам. Уничтожение одного из временных направлений позволяет М-теории породить одиннадцатимерную супергравитацию непосредственно в одиннадцатимерном пространстве, а на его десятимерной «коже» создать теории суперструн. Здесь имеются различные возможности: либо одиннадцатое измерение сворачивается в окружность очень малого радиуса R (тогда изображенный на рисунке цилиндр имеет на самом деле десять измерений), либо М-теория выделяет две десятимерные гиперплоскости на расстоянии порядка R друг от друга в одиннадцатимерном пространстве. В зависимости от того, какая возможность выбрана, получающееся пространство населяется (в качестве остатков от М-теории) суперструнами одного из пяти видов (наглядно объяснить различие между ними не представляется возможным). Эти-то суперструны далее предписывают десятимерному пространству, как свернуть лишние шесть измерений.

ВТОРАЯ КООРДИНАТА ВРЕМЕНИ

Суперструны, однако, «помнят» про свое единое происхождение из М-теории: учет всех намоток струн показывает, что различные пространства эквивалентны с точки зрения эффектов, осевших на четырехмерной «коже» этого безумного мира. В конечном итоге именно М-теория ответственна за свойства нашего четырехмерия, а современные средства исследования позволяют наметить путь от нее к привычному нам миру, используя любую из пяти теорий суперструн.

Возможности М-теории не ограничиваются производством десятимерии и вселением туда суперструн. Она могла бы развиться в мир, совершенно непохожий на наш, где вместо структур пространства-времени (пусть даже «свернутых») имелся бы «первичный бульон» из мембран и «многобран» различной размерности. Отыскать механизмы, управляющие динамикой М-теории, видимо, удастся уже в XXI веке. Пока же название «М-теория» вполне оправдывает свое происхождение от слова mystery.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.