Фантомные космологии и космический судный день
Открытие Хабблом космологического расширения совместно с математическими предсказаниями Фридмана (и других) в рамках ОТО вызвали многочисленные предсказания о конечной судьбе Вселенной. В частности, было показано, что если материю, заполняющую Вселенную, рассматривать как жидкость без давления, (такое возможно применительно к галактикам) то: (1) если Вселенная имеет Эвклидову или плоскую пространственную геометрию она расширяется всегда; (2) если геометрия Вселенной эквивалентна 3-сфере, то в конце концов наступает реколлапс. Целый ряд выполненных в последнее время наблюдений (SNe, CMB, WMAP и другие) показали, что расширение происходит ускоренно и, следовательно, такая простая картина не достаточна. Вселенная дополнительно содержит дополнительную компоненту – темную энергию с отрицательным давлением.
В статье обсуждается динамика минимально связанных скалярных полей в расширяющейся Вселенной с ударением на так называемую фантомную космологию. Эволюция Вселенной, управляемая фантомным полем, сравнивается с эволюцией, обязанной квинтэссенции.
Фантомные космологии имеют две отличительные особенности: 1) возникновение сингулярности, при которой масштабный фактор, плотность энергии и скаляр кривизны Риччи обращаются в бесконечность; сингулярность возникает на конечных временах, зависящих от значения $w$ в процессе космической эволюции. 2) вырождение в определении $w(z_m)$ для данного переходного значения космологической постоянной $z_m$, придающее одинаковые наблюдательные свойства моделям, базирующимся как на фантомной энергии, так и на квинтэссенции; это вырождение делает оба типа моделей совместимыми с космологическими наблюдениями. Хотя благодаря неопределенности в измерении хаббловской константы $H_0$, мы имеем слишком широкий интервал значений $w$, дуальность в определении $w$ по отношению к переходному красному смещению использована для определения $w.$ Тест, базирующийся на наблюдении галактических кластеров с низкими значениями красного смещения, можно использовать для выбора между фантомной энергией и квинтэссенцией.
Введение
Комбинированный анализ SN 1а (сверхновых звёзд типа 1а), динамики галактических кластеров и анизотропии реликтового излучения обеспечивает убедительное доказательство существования темной энергии, которая доминирует во Вселенной в настоящее время и ускоряет космическое расширение. Недавнее детектирование интегрального эффекта Сакса-Вольфа дало дополнительные сильные и независимые доказательства в пользу тёмной энергии. В принципе, любое физическое поле с положительной плотностью энергии и отрицательным давлением, нарушающее сильное энергетическое условие (СЭУ), может являться источником основного эффекта – гравитационного отталкивания. Недавно появился новый кандидат на роль темной энергии – фантомная энергия. Скалярное поле с суперотрицательным уравнением состояния $(p=w\rho, w<-1)$ называется фантомным полем, так как его плотность энергии увеличивается при расширении Вселенной, в противоположность плотности энергии квинтэссенции $(w>-1),$ убывающей при космическом расширении. Фантомные модели нарушают условие энергодоминантности (DEC) $(p+\rho <0).$ По этой причине они не могут быть физически устойчивыми моделями темной энергии. Тем не менее, достаточно странно, но найдено, что фантомная энергия совместима с большинством классических тестов космологии.
Специфическая особенность фантомной энергии – нарушение условия энергодоминантности и ее странные следствия: возможный разрыв больших и малых структур материи, возникновение будущих сингулярностей и возможный распад фантомной энергии привлекли внимание многих космологов и сделали фантомную энергию горячей точкой физических исследований.
Динамика фантомной космологии
Рассмотрим в рамках уравнений Фридмана 2-х компонентную космическую жидкость, состоящую из (i) материи без давления с плотностью энергии ${{\rho }_{m}}$ и (ii) минимально связанное скалярное поле с плотностью энергии ${{\rho }_{x}}$ и уравнением состояния ${{p}_{x}}=w{{\rho }_{x}}$. Это поле дает вклад в темную энергию Вселенной. Плотности энергии ${{\rho }_{m}}\sim {{a}^{-3}}$ и ${{\rho }_{x}}\sim {{a}^{-3(1+w)}}$ независимо эволюционируют в расширяющейся Вселенной.
Темная энергия может быть обязана:
(а) полю квинтэссенции, если $-1<w<-1/3$;
(b) космологической константе, если $w=-1$;
(с) фантомному полю, если $w<-1$.
В приведенной выше классификации параметр уравнения состояния $w$ играет роль параметра, определяющего компоненту, представляющую темную энергию.
Уравнения Фридмана
\[\frac{{{{\dot{a}}}^{2}}}{{{a}^{2}}}=\frac{8\pi G}{3}\left[ {{\rho }_{m}}+{{\rho }_{x}} \right]=H_{0}^{2}\left[ \Omega _{m}^{0}{{\left( {{a}_{0}}/a \right)}^{3}}+\Omega _{x}^{0}{{\left( {{a}_{0}}/a \right)}^{3(1+w)}} \right];{{\Omega }_{i}}=\frac{{{\rho }_{i}}}{{{\rho }_{crit}}};\ {{\rho }_{crit}}=\frac{3H_{0}^{2}}{8\pi G}\]
(1)
и\[\frac{{\ddot{a}}}{a}=-\frac{4\pi G}{3}\left[ {{\rho }_{m}}+{{\rho }_{x}}(1+3w) \right]=-\frac{4\pi G}{3}{{\rho }_{x}}\left[ \Omega _{x}^{-1}+3w \right]=-\frac{4\pi G}{3}{{\rho }_{x}}\left[ \frac{\Omega _{m}^{0}}{\Omega _{x}^{0}}{{\left( \frac{{{a}_{0}}}{a} \right)}^{-3w}}+1+3w \right]\]. (2)
Космическое расширение замедляется до тех пор, пока
\[\Omega _{x}^{-1}+3w>0\] (3)C ростом фантомной энергии параметр $\Omega _{x}^{-1}$ уменьшается и в конце концов наступает переход к фазе ускоренного расширения в космическое время $t={{t}_{m}}$. Время перехода${{t}_{m}}$ соответствует красному смещению ${{z}_{m}}$, задаваемому соотношением
\[1+{{z}_{m}}={{\left[ \frac{-(3w+1)\Omega _{x}^{0}}{\Omega _{m}^{0}} \right]}^{-\frac{1}{3w}}}\] (4)
Следует подчеркнуть, что переходная эпоха ${{t}_{m}}$ знаменует конец эры доминирования материи и начало фазы ускоренного космического расширения, после которого образование космологических структур (галактик и их скоплений) во Вселенной должно прекратиться, хотя ${{\Omega }_{m}}$ может еще быть больше ${{\Omega }_{x}}$. Из соотношения (4) очевидно, что переходное время ${{t}_{m}}$ зависит от выбора $w$. Вариации ${{z}_{m}}$ при изменении $w$ представлены на Рис.3.
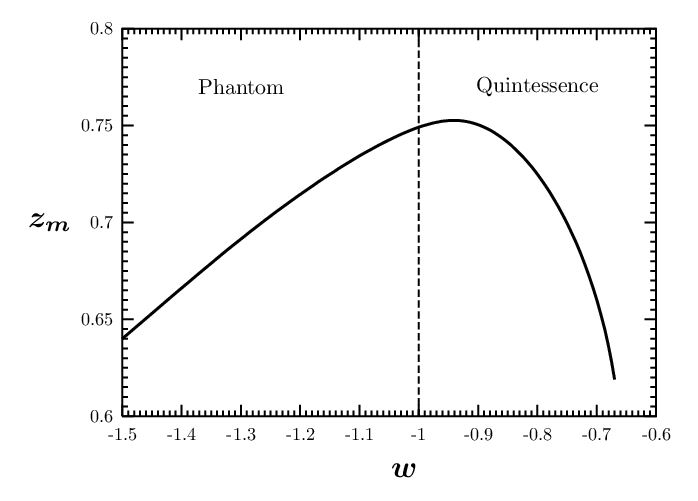
По мере уменьшения $\Omega _{x}^{-1}$ после переходной эпохи
\[\Omega _{x}^{-1}+3w<0\] (5)
и хаббловское расширение в ускоренной (выбранный параметр $\Omega _{m}^{0}/\Omega _{x}^{0}$) фазе расширения Вселенной задается уравнением (1)
\[\frac{{\dot{a}}}{a}={{H}_{0}}\sqrt{\Omega _{x}^{0}}{{\left( \frac{{{a}_{0}}}{a} \right)}^{3(1+w)/2}}{{\left[ 1+\frac{\Omega _{m}^{0}}{\Omega _{x}^{0}}{{\left( \frac{a}{{{a}_{0}}} \right)}^{3w}} \right]}^{1/2}}\] (6)
Раскладывая корень (и дробь) по параметру $\Omega _{m}^{0}/\Omega _{x}^{0}{{\left( a/{{a}_{0}} \right)}^{3w}}$ и выполняя интегрирование, получим
\[\chi t+c={{\left( \frac{a}{{{a}_{0}}} \right)}^{3(1+w)/2}}\left[ \frac{2}{3(1+w)}-\frac{\Omega _{m}^{0}{{a}^{3w}}}{\Omega _{x}^{0}a_{0}^{3w}\left( 9w+3 \right)}+\cdots \right]\] (7)
где $\chi ={{H}_{0}}\sqrt{\Omega _{x}^{0}}$. Разложение в ряд правой стороны (6) действительно при выполнении условия $\frac{\Omega _{m}^{0}}{\Omega _{x}^{0}}{{\left( \frac{a}{{{a}_{0}}} \right)}^{3w}}<1$.
Ускоренное расширение возможно и в случае ${{\Omega }_{m}}>{{\Omega }_{x}}$при выполнении условия $-(3w+1)\Omega _{x}^{0}>{{\Omega }_{m}}$.
При $w<0$ последовательные члены в (7) быстро убывают и масштабный фактор эффективно задается выражением
Это выражение показывает, что вклад плотности материи пренебрежимо мал во Вселенной, в которой доминирует фантомная энергия, так как вклад $\Omega _{m}^{0}$ падает как третья степень малого параметра в каждом последующем члене (7). Согласно (1) космическое расширение в ускоряющей фазе существенно управляется фантомной энергией, так как ее плотность растет как ${{\rho }_{x}}\sim {{a}^{-3(1+w)}}$, в то время как плотность энергии обычной материи падает как $\sim {{a}^{-3}}$. $$
В течение фазы замедленного ускорения
\[\frac{{\dot{a}}}{a}={{H}_{0}}\sqrt{\Omega _{m}^{0}}{{\left( \frac{{{a}_{0}}}{a} \right)}^{3/2}}{{\left[ 1+\frac{\Omega _{x}^{0}}{\Omega _{m}^{0}}{{\left( \frac{a}{{{a}_{0}}} \right)}^{3w}} \right]}^{1/2}}\] (9)
Замедленнее подразумевает, что $\frac{\Omega _{x}^{0}}{\Omega _{m}^{0}}{{\left( \frac{{{a}_{0}}}{a} \right)}^{3w}}<1$. Разлагая (9) в ряд по малому параметру и интегрируя получим
\[\xi t={{a}^{3/2}}\left[ \frac{2}{3}-\frac{{{(1+z)}^{3w}}\Omega _{x}^{0}}{3(1-2w)\Omega _{m}^{0}}+\frac{{{(1+z)}^{6w}}}{4(1-4w)}{{\left( \frac{\Omega _{x}^{0}}{\Omega _{m}^{0}} \right)}^{2}}+\cdots \right]\] (10)
$\xi ={{H}_{0}}\sqrt{\Omega _{m}^{0}}$. Так как $w<0$, то первый член в правой части доминирует при переходе к большим красным смещениям. Следовательно в течение эры доминирования материи
\[{{a}^{3/2}}(t)=\frac{3}{2}\xi t\] (11)Это соотношение справедливо при $t={{t}_{m}}$, так что
\[{{a}^{3/2}}({{t}_{m}})=\frac{3}{2}\xi {{t}_{m}}\] (12)В начале фазы доминирования темной энергии соотношение (8) дает
\[{{a}^{3(1+w)/2}}({{t}_{m}})=\frac{3}{2}\chi {{t}_{m}}+c\] (13)Выполняя сшивку при $t={{t}_{m}}$ из (12) и (13) получим
\[{{\left[ \frac{a(t)}{a({{t}_{m}})} \right]}^{3(1+w)/2}}=1+\frac{3/2(w+1)\chi (t-{{t}_{m}})}{{{a}^{3(1+w)/2}}({{t}_{m}})}=1+(w+1)\frac{t-{{t}_{m}}}{{{t}_{m}}}\] (14)Следовательно, масштабный фактор во Вселенной, в которой доминирует фантомная (темная) энергия эволюционирует как
\[a(t)=\frac{a({{t}_{m}})}{{{\left[ -w+(1+w)t/{{t}_{m}} \right]}^{-\frac{2}{3(1+w)}}}},\quad t>{{t}_{m}}\] (15)
Так как $1+w<0$ для фантомных полей, то $a(t)$ обращается в бесконечность при
\[t*=\frac{w}{1+w}{{t}_{m}}\]
В противоположность случаю фантомной энергии, в случае квинтэссенции $1+w>0$и космическое расширение свободно от сингулярности с масштабным фактором
\[a(t)=a({{t}_{m}}){{\left[ 1+(1+w)\left( t-{{t}_{m}} \right)/{{t}_{m}} \right]}^{\frac{2}{3(1+w)}}}\]
.
Используя (15), получим, что плотность фантомной энергии во Вселенной при $t>{{t}_{m}}$ задается соотношением
\[{{\rho }_{x}}(t)=\frac{\rho ({{t}_{m}})}{{{\left[ -w+(1+w)t/{{t}_{m}} \right]}^{2}}}\] (16)
Согласно (16) ${{\rho }_{x}}$ постоянно растет, обращаясь в бесконечность при ${{t}^{*}}=\frac{w}{1+w}{{t}_{m}}$. Следовательно фантомные модели имеют конечное время жизни достижения сингулярности. С другой стороны, ${{\rho }_{x}}$ уменьшается во времени во Вселенной с квинтэссенцией и остается постоянной в случае космологической константы. Для $t<{{t}_{m}}$ хаббловское расширение доминируется плотностью материи. При этом $a\sim {{t}^{2/3}},\ {{\rho }_{m}}\sim {{t}^{-2}}$, а${{\rho }_{x}}$ изменяется независимо как ${{t}^{-2(1+w)}}$, как показано на Рис.2.
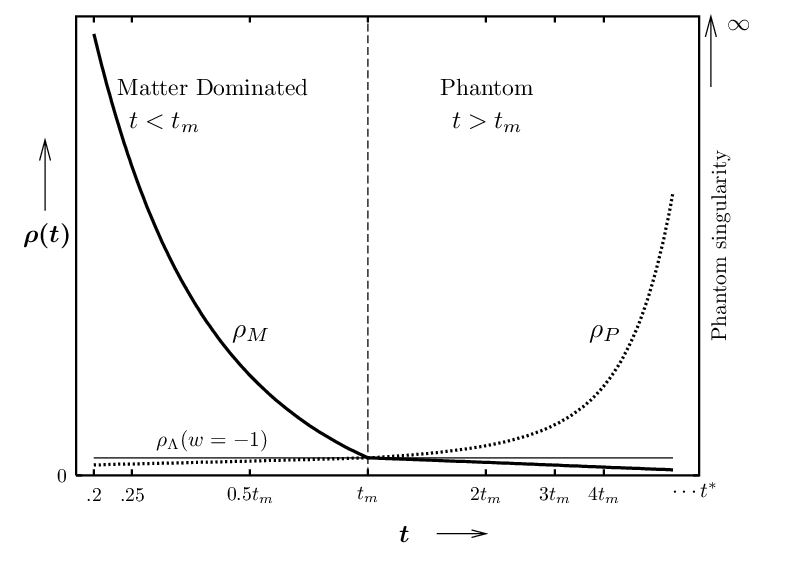
Сингулярность в масштабном факторе и плотности энергии для фантомной Вселенной соответствует сингулярности в кривизне ($R_{i}^{i}$-шпуре тензора Риччи), обращающейся в бесконечность в эту же эпоху. Полный возраст ${{t}^{*}}$ фантомной Вселенной зависит от выбора $w$ и растет при приближении $w$ к $-1$. Например, ${{t}^{*}}=21{{t}_{m}}$ для $w=-1.05$, в то время как ${{t}^{*}}=6{{t}_{m}}$ для $w=-1.2.$
Что же происходит за границей w<-1?
Для этой области темных энергий даже придуман специальный термин - фантомная энергия. В этой области нарушается слабое условие энергодоминантности $(P+\rho< 0).$ Такое же нарушение энергодоминантности требуется для существования "кротовых нор", из которых можно создать машину времени. Но в космологии нарушение этого условия приводит к совсем другим следствиям, которые составляют основные выводы данной статьи, и именно они вызвали интерес прессы.
  |
|
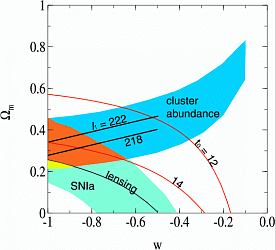
Рис. 1.
Современные наблюдательные ограничения для космологических параметров,
показанные на плоскости $\Omega_m$--$w$. Сплошные красные
кривые соединяют точки равных возрастов Вселенной (12 и 14
млрд. лет).
Параметры в закрашенных областях допустимы по наблюдениям скоплений
галактик и сверхновых. Ярко оранжевым и желтым цветами показаны области
их пересечения. Черные сплошные линии показывают дополнительные
ограничения, вытекающие из наблюдений гравитационного линзирования
квазаров (кривая) и из положения первого акустического пика в спектре
мощности анизотропии реликтового излучения (прямые линии, отмеченные
числами 218 и 222).
На левом рисунке показана диаграмма, ограниченная условием
w>-1, как ее обычно и изображают. Справа - та же
диаграмма, продолженная в область фантомных энергий. Видно, что есть
область параметров с w<-1, удовлетворяющая наблюдениям.
Штрих-пунктирные линии на правом рисунке соответствуют одинаковым
значениям момента "Большого Разрыва".
(Диаграммы построены для значения постоянной Хаббла H0=70 км/с/Мпк, закрашенные области построены для уровня значимости $2\sigma.)$ |
 |
Рис. 2.
Несколько возможных сценариев расширения Вселенной. Снизу вверх:
|
Посмотрим, какую судьбу предсказывают Вселенной различные космологические сценарии.
В плоской и открытой Фридмановских моделях (без темной энергии) расширение продолжается бесконечно, но замедляется. При этом размер горизонта (области, доступной для наблюдения) увеличивается быстрее, чем масштабный фактор Вселенной. По мере расширения Вселенная становится более холодной (падает температура реликтового излучения) и более темной (источники света - галактики и их скопления - удаляются). Однако число видимых галактик (внутри горизонта) возрастает - вблизи горизонта "появляются" новые, ранее не наблюдавшиеся объекты.
Во Вселенной с темной энергией (-1<w<1/3) расширение ускоряется. Этот процесс длится вечно. Вселенная также становится темнее и холоднее, но в этом случае размеры Вселенной возрастают быстрее, чем горизонт. Из видимой области постепенно будут исчезать объекты, расположенные вблизи горизонта. В конце концов "в центре" наблюдаемой области Вселенной останется только один гравитационно связанный объект. Для нас это будет местная группа галактик. Судьба галактик, не входящих в группы и скопления, будет еще более одинокой. Давление и плотность заполняющего Вселенную вещества убывают со временем. Исключением является предельный случай с $\Lambda$-членом (w=-1), когда и давление, и плотность вещества остаются постоянными.
Прежде чем перейти к рассмотрению судьбы Вселенной в сценарии с призрачной энергией, надо обсудить вопрос о судьбе гравитационно (и не только) связанных объектов, поскольку это важно. Согласно Общей Теории Относительности, источником гравитационного поля являются как плотность вещества, так и его давление, а точнее, следующая их комбинация $\rho+3p$ (для изотропных сред). Пусть, как мы и рассматриваем, все пространство заполнено таким веществом, тогда тело (например, планета) обращающееся вокруг звезды с массой M по орбите радиуса R, перестанет быть гравитационно связанным со звездой при выполнении условия
$$ -\frac{4\pi}{3} (\rho+3p)R^3 \gtrsim M\,.$$Из этого выражения ясно, что "фоновая" материя делает системы менее связанными, если $\rho+3p< 0$, т.е. Вселенная должна быть заполнена темной или фантомной энергией (w<-1/3).
В сценарии с темной энергией ее давление и плотность с течением времени убывают, поэтому объекты, которые являются связанными (гравитацией или другими силами) сегодня, будут оставаться такими и в будущем.
Если Вселенную заполняет фантомная энергия (w<-1), то ее масштабный фактор обращается в бесконечность за конечный интервал времени. Это событие авторы статьи назвали "Большой Разрыв" (Big Rip) [почему разрыв - смотрите ниже] - по аналогии с Большим Взрывом (Big Bang). (Здесь присутствует игра слов: Rip - разрыв, RIP - аббревиатура от Remain In Peace ["Покойся с миром"] - типичной английской эпитафии.) Если в качестве примера взять w=-3/2, то при H0=70 км/с/Мпк Большой Разрыв наступит через 22 млрд.лет (когда Вселенной будет 35 млрд.лет). Так же, как и в сценарии с темной энергией, удаленные объекты постепенно покидают наблюдаемую область, поскольку масштабный фактор быстро возрастает, а граница обозримой области пространства приближается к нам (и все это происходит за конечное время). В этом сценарии плотность и абсолютная величина давления заполняющего пространство вещества (призрачной энергии) возрастают со временем и к моменту Большого Разрыва обращаются в бесконечность, комбинация $\rho+3p$ становится все более и более отрицательной. Таким образом, обязательно наступит момент, когда гравитационно связанная система с массой M и размером R будет разорвана (распадется). Это произойдет неизбежно, от параметров системы зависит только момент ее разрыва. Будут разорваны и все системы, связанные другими силами, только это произойдет позже, поскольку размеры негравитационно связанных систем меньше, а скрепляющие их силы - мощнее. (Отсюда и взялось название Большой Разрыв.)
Для указанных выше параметров (w=-3/2 и H0=70 км/с/Мпк) жизнь Вселенной - от Big Bang до Big Rip - выглядит так:
| Время | Событие |
| 0 | Большой Взрыв |
| ~10-43 с | Планковская эра |
| ~10-36 с | Инфляция |
| ~100 с | Первичный нуклеосинтез |
| ~105 лет | Образование атомов |
| ~109 лет | Образование первых галактик |
| ~15.109 лет | Сегодня |
| trip-109 лет | Распад скоплений галактик |
| trip-60.106 лет | Распад Млечного Пути * |
| trip-3 месяца | Распад Солнечной системы |
| trip-30 минут | Разрушение (взрыв) Земли |
| trip-10-19 c | Разрушение атомов |
| trip=35.109 лет | Большой Разрыв |
| * Когда начнется распад галактик, размер горизонта будет около 70 Мпк. В этой сфере заключено достаточно много галактик, так что мы сможем наблюдать, как они распадаются (с учетом задержки, связанной с конечностью скорости света). | |

Аналогичные аргументы применимы к объектам, связанным электромагнитным или сильным взаимодействием. Поэтому молекулы и затем атомы распадутся за времена порядка ${{10}^{-19}}$ секунды до Большого Разрыва , а в оставшееся время распадутся ядра и нуклоны (нужно просто в качестве $T$ подставлять характерные времена). Разумеется, возможно, что новая физика (спонтанное рождение частиц, дополнительные размерности, струны и/или квантовая гравитация) ворвется до наступления окончательной сингулярности, но, скорее всего, это будет после перечисленной последовательности событий.
Конец всех структур, от макро до микроскопических, делает очевидным то, что наша эпоха уникальна с точки зрения того, что в другое время невозможно существование (non-linear) структур. Когда фантомная энергия становится достаточно сильной, гравитационная нестабильность больше не работает и Вселенная становится однородной. В конце концов индивидуальные частицы станут изолированными: точки, разделенные расстоянием больше $3\delta t(1+w)/(1+3w)$ во время ${{t}_{rip}}-\delta t$ не смогут связаться до Big Rip. Следовательно, доминирование фантомной энергии сигнализирует о конце нашей короткой эры космических структур, которая началась, когда нерелятивистская материя «отсоединилась» от излучения. В такой Вселенной некоторые космические вопросы приобретают новый смысл.
Естественно обнаружить себя (или в более широком смысле нелинейные структуры) живущими достаточно близко к моменту начала ускорения, если эти структуры вскоре разрушатся и Вселенная после этого долго не выживет. Во Вселенной, которую ожидает Big Rip, вопрос «почему теперь?» (или проблема космических совпадений) неуместен. Только в момент начала ускорения такие структуры и могут существовать. Вчера было рано, а сегодня уже поздно. Текущие данные указывают на то, что наша Вселенная балансирует в узкой области на границе между фантомной энергией, космологической константой и квинтэссенцией. Будущие наблюдения помогут определить природу темной энергии. Мы заинтригованы новой судьбой Вселенной, которая существенно отличается от реколлапса или бесконечного охлаждения, рассматриваемых ранее. Нам придется модифицировать известное изречение Роберта Фроста: «Некоторые говорят, что мир погибнет в огне, некоторые говорят во льду». Видимо, мир ждет другая судьба.
Что можно добавить к изложению результатов, приведенных в статье ?
- Чисто теоретически показано, что кроме давно предсказанных вариантов "судьбы" нашей Вселенной - сжатия с последующим коллапсом или бесконечного расширения, найдена еще одна возможность - Большой Разрыв. На сегодняшний день это только интересная теоретическая идея, каких-либо серьезных указаний на возможность реализации подобного сценария нет.
- Из самых общих соображений ясно, что никакая физика не сможет заставить вещество обладать свойствами призрачной энергии до момента Большого Разрыва. Его свойства изменятся, и далее расширение Вселенной пойдет по-другому. Однако нельзя заранее сказать, как близко к Большому Разрыву она подойдет и какие тела в ней еще сохранятся.
Нет комментариев.
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.






