Уравнение Дирака для электрона стало для физики поворотным пунктом во многих отношениях. В 1928 году, когда Дирак предложил свое уравнение, из всех элементарных частиц науке были известны лишь электроны, протоны и фотоны. Свободные уравнения Максвелла описывают фотоны, предсказанные Эйнштейном в 1905 году. Эта ранняя работа была постепенно развита Эйнштейном, Бозе и другими, и 1927 году Иордан и Паули создали полную математическую схему для описания свободных фотонов путем введения квантования в максвелловскую теорию свободного поля. Казалось также, что протон, как и электрон, достаточно хорошо описывается уравнением Дирака. В теорию Дирака отлично укладывалось электромагнитное взаимодействие, описывающее, как воздействуют фотоны на электроны и протоны, благодаря идее калибровки (введенной Вейлем в 1918 году). Начало формулировке полной теории электронов (или протонов), взаимодействующих с фотонами (т.е. квантовой электродинамике), было положено самим Дираком в 1927 году . Таким образом, казалось, что имеются под руками все более или менее основные средства для описания всех частиц, существующих в Природе, а также наиболее очевидных взаимодействий между ними.

Истоки современной физики элементарных частиц

И все же физики того времени в большинстве своем были не настолько глупы,  чтобы предполагать, что все это вот-вот приведет их к «теории всего». Они сознавали, что ни силы, удерживающие ядро от распада (ныне это называется сильным  взаимодействием), ни механизм, ответственный за радиоактивный распад (теперь это называется слабым взаимодействием), не могут быть объяснены без дальнейшего продвижения вперед. Если бы единственными составными частями атомов, включая атомные ядра, были дираковские протоны и электроны, взаимодействующие лишь через электромагнитное поле, тогда все обычные ядра (за исключением одиночного протона, составляющего ядро атома водорода) должны были мгновенно распадаться из-за электростатического отталкивания вследствие преобладания положительных зарядов. Должно было существовать нечто дотоле не  известное, создающее сильное притяжение между частицами внутри ядра!

В 1932 году Чедвик открыл нейтрон, и это в итоге привело к замене ранее популярной протонно-электронной модели ядра новой моделью, согласно которой ядро содержит протоны и нейтроны, сильное взаимодействие между которыми удерживает ядро от распада. Но даже это сильное  взаимодействие было еще не все, что ускользало от понимания в то время. Радиоактивность урана, известная со времени наблюдения Анри Беккереля в 1896 году, оказалась результатом еще одного — слабого — взаимодействия, отличного и от сильного, и от электромагнитного взаимодействия. Даже сам нейтрон, будучи предоставлен самому себе, распадается  приблизительно за 15 минут.

Одним из загадочных продуктов радиоактивного распада оказалось неуловимое нейтрино, пробная гипотеза о существовании которого была выдвинута Паули в 1929 году, но которое не было непосредственно обнаружено вплоть до 1956 года. Именно изучение радиоактивности в конечном счете принесло физикам неожиданную популярность и влиятельность к концу Второй мировой войны и после нее...

Многое изменилось с той поры первоначального проникновения в физику  элементарных частиц в первой трети XX века. Сейчас, в начале XXI века, мы имеем гораздо более полную картину, известную под названием стандартной модели физики элементарных  частиц. Эта модель описывает почти все наблюдаемое поведение широкого класса известных ныне элементарных частиц. К фотону, электрону, протону, позитрону, нейтрону и  нейтрино в дальнейшем присоединились разные другие сорта нейтрино, мюон, пионы (эффектно предсказанные Юкавой в 1934 году), каоны, ламбда- и сигма-частицы, а также омега-минус- частица, знаменитая благодаря истории ее предсказания. В 1955 году был экспериментально обнаружен антипротон, в 1956 году — антинейтрон. Существуют объекты нового типа — кварки, глюоны и W- и Z-бозоны, а также целая стая частиц, существование которых столь быстротечно, что они никогда не наблюдались непосредственно, их относят к «резонансам». Формализм современной теории требует также существования нестационарных объектов, называемых «виртуальными частицами», а также величин, именуемых «духами»,  относительно которых исключается возможность непосредственного наблюдения.

Существует  также вызывающее замешательство изобилие гипотетических (и пока не обнаруженных) частиц, предсказываемых некоторыми теоретическими моделями, но пока не укладывающихся в  общепринятую схему элементарных частиц, — «Х-бозоны», «аксионы», «фотино», «скварки», «глюино», «магнитные монополи», «дилатоны» и т. д. Есть еще призрачная частица Хиггса, не обнаруженная к моменту написания этой книги, существование которой в той или иной форме (возможно, не в качестве одиночной частицы) существенно для сегодняшней физики элементарных частиц, в которой связанное с этой частицей поле Хиггса определяет массу каждой элементарной частицы.

Зигзаг-представление электрона

В этой и ряде последующих статей предлагается краткий путеводитель по стандартной модели современной физики элементарных частиц.
Начнем несколько нестандартным образом, переформулировав уравнение Дирака в «2-спинорном представлении. Спинор Паули, описывающий частицу со спином -, представляет собой двухкомпонентную величину $\psi_a$- (Компонентами служат $\psi_0$-  и $\psi_1$.) При учете  требований теории относительности нам потребуются также величины со штрихованными индексами  $A', B', C’$,..., которые появляются при комплексном  сопряжении, применяемом к нештрихованным индексам. Оказывается, что описанный выше дираковский спинор $\psi$ с его четырьмя комплексными компонентами можно представить в виде пары 2-спиноров,  $\alpha_a$ и $\beta_{a’}$, один из которых имеет нештрихованный индекс, а другой — штрихованный:
$$\psi=(\alpha_a,\beta_{a’}) $$

Тогда уравнение Дирака можно записать в виде уравнения, связывающего эти два 2-спинора, при этом каждый из них играет в отношении другого роль «источника» с «константой связи» $2^{-1/2}M$, определяющей «силу взаимодействия» между ними:
$$\nabla^{A}_{B’ }\alpha_a =2^{-1/2}M\beta_{B’}, ~~\nabla ^{B’}_{A }\beta_{B’} =2^{-1/2}M,\alpha _{A’}, $$

Операторы $\nabla^{A}_{B’ }$, и $\nabla^{B}_{A’ }$  представляют собой 2-спинорные трансляции обычного  оператора градиента $\nabla$  . Не следует придавать большого значения всем этим индексам,  множителям $2^{-1/2}$ и точной форме этих уравнений, — я привожу их здесь лишь для того, чтобы показать, как можно ввести уравнение Дирака в общие рамки 2-спинорного анализа и как это может помочь, коль скоро это сделано, в обретении некоторого нового взгляда на природу уравнения Дирака.

Форма этих уравнений показывает, что дираковский электрон можно считать  состоящим из двух ингредиентов — $\alpha_A$ и $\beta_{A’}$.  Им можно придать некоторый физический смысл.

Можно представить себе картину, в которой существуют две «частицы», одна из которых описывается величиной а  $\alpha_A$  а другая — $\beta_{A’}$, причем обе они не имеют массы и каждая из них непрерывно превращается в другую. Дадим этим частицам имена «зиг» и «заг», так что   $\alpha_A$ будет описывать частицу «зиг», а $\beta_{A’}$ — частицу «заг». Будучи безмассовыми, они должны перемещаться со скоростью света, однако вместо этого можно считать, что они «качаются» взад-вперед, причем движение вперед частицы «зиг» непрерывно  превращается в движение назад частицы «заг» и наоборот. Фактически это есть реализация явления, называемого «zitterbewegung» («дрожание») и состоящего в том, что мгновенное движение электрона из-за участия в таких колебаниях всегда происходит со скоростью света,  хотя полное усредненное движение электрона характеризуется скоростью, меньшей скорости света.  Каждый из указанных ингредиентов имеет спин величиной $\frac{1}{2}\hbar$ в направлении  движения, соответствующий левому вращению в случае частицы «зиг» и правому для частицы «заг». (Это связано с тем обстоятельством, что частица «зиг» $\alpha_A$  имеет нештрихованный  индекс, соответствующий отрицательной спиральности, а частица «заг» $\beta_{A’}$ — штрихованный индекс, отвечающий положительной спиральности.

Заметим, что хотя скорость все время меняется, направление спина в системе покоя электрона остается постоянным (рис. 1). При такой интерпретации частица «зиг» выступает как источник для частицы «заг», а частица «заг» — как источник в отношении частицы «зиг», сила связи между ними определяется величиной $M$.

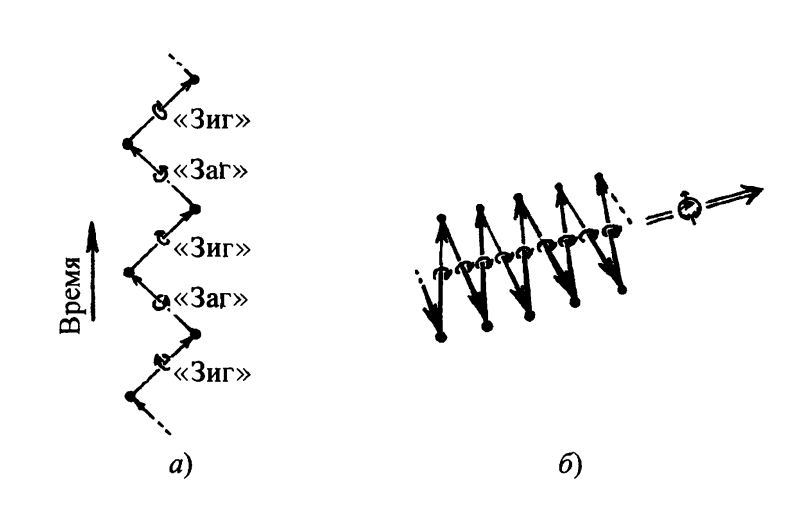
Рис. 1. Зигзаг-представление электрона, а) Электрон (или другую массивную частицу со спином $\frac{1}{2}\hbar$ ) можно рассматривать как осциллирующую в пространстве-времени между безмассовой частицей «зиг» с левой спиральностью (спиральность $-\frac{1}{2}$ описывается нештрихованным 2-спинором $\alpha_A$ или, в обозначениях, более привычных для физиков, частью, проектируемой оператором -$\frac{1}{2}(1-\gamma_5)$)) и безмассовой частицей «заг» с правой спиральностью (спиральность $+\frac{1}{2}$ описывается штрихованным 2-спинором $\beta_{A'}$ или частью, проектируемой оператором $\frac{1}{2}(1+\gamma_5)$. Каждая из частиц служит источником для другой с массой покоя в качестве константы связи, б) С точки зрения 3-пространства, в системе покоя электрона происходит непрерывное изменение скорости (всегда равной по величине скорости света), однако направление спина остается постоянным. (Для большей наглядности изображена картина не вполне в системе покоя электрона — вместо этого электрон медленно смещается вправо.)

На рис. 2 дано диаграммное представление вклада этого процесса в полный «фейнмановский пропагатор. Каждый отдельный зигзаг-процесс имеет   конечную длину, однако вся их совокупность, включающая зигзаги все нарастающей длины, дает вклад в полный процесс распространения электрона в соответствии с матрицей $2\times2$, изображенной на рис. 2. При этом частица «зиг» становится частицей «заг», затем «заг» превращается в «зиг», та снова в «заг» и так далее на некотором конечном отрезке. 

Рассматривая процесс в целом, мы обнаружим, что средняя частота, с которой это происходит, связана обратным соотношением с параметром связи — массой М; фактически это есть «де-бройлевская частота» электрона.
Необходимо, однако, сделать замечание относительно того, как следует  интерпретировать фейнмановские диаграммы. Изображаемый процесс можно на законных основаниях рассматривать как пространственно-временное описание происходящего, однако при рассмотрении на квантовом уровне необходимо иметь в виду, что даже в случае одной частицы одновременно протекает множество таких процессов. Каждый из них следует  рассматривать как один из вкладов в некоторую квантовую суперпозицию огромного числа различных процессов. Реальное квантовое состояние определяется всей суперпозицией в целом. Каждая отдельная фейнмановская диаграмма — это всего лишь одна из ее  компонент.

Необходимо, однако, сделать замечание относительно того, как следует  интерпретировать фейнмановские диаграммы. Изображаемый процесс можно на законных основаниях рассматривать как пространственно-временное описание происходящего, однако при   рассмотрении на квантовом уровне необходимо иметь в виду, что даже в случае одной  частицы одновременно протекает множество таких процессов. Каждый из них следует  рассматривать как один из вкладов в некоторую квантовую суперпозицию огромного числа различных процессов. Реальное квантовое состояние определяется всей суперпозицией в целом. Каждая отдельная фейнмановская диаграмма — это всего лишь одна из ее  компонент.

В таком же духе следует понимать и приведенное выше описание движения электрона как качания взад-вперед, при котором «зиг» непрерывно превращается в «заг» и наоборот. Реальное движение слагается из большого (фактически бесконечно большого) числа таких отдельных процессов, так что наблюдаемое движение электрона можно рассматривать как результат некоторого их «усреднения» (хотя, строго говоря, здесь имеет место квантовая суперпозиция). Так обстоит дело в случае всего лишь свободного электрона. В   действительности электрон непрерывно взаимодействует с другими частицами (например, с фотонами — квантами электромагнитного поля). Все подобные процессы взаимодействия также должны быть включены в общую суперпозицию.  

Имея все это в виду, зададимся вопросом: насколько «реальны» частицы «зиг» и «заг»? Или это всего лишь артефакты некоторого математического формализма, которым я вос пользовался здесь при описании уравнения Дирака для электрона? Возникает вопрос более общего характера: насколько оправданно с физической точки зрения руководствоваться   соображениями изящества некоторого математического описания, а затем пытаться выдать это за описание «реальности»? В данном случае следует начать с постановки вопроса о   важности (а также изяществе) самого 2-спинорного формализма как математического метода. Я должен предупредить читателя, что этот формализм не относится к числу широко   используемых физиками, которые занимаются уравнением Дирака и его приложениями, в   частности, квантовой электродинамикой (КЭД) — наиболее успешным разделом квантовой теории поля.

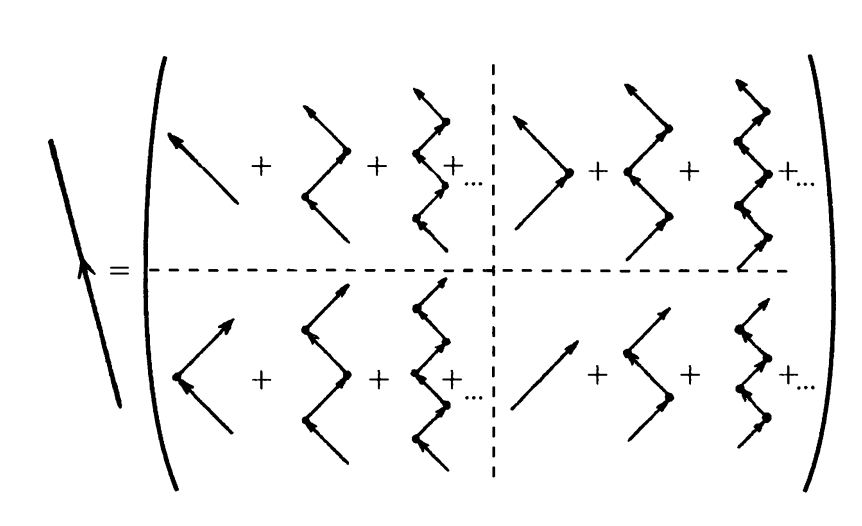
Рис.2. Каждый зигзаг-процесс в отдельности вносит вклад, как часть бесконечной квантовой суперпозиции, в полный «пропагатор» наподобие фейнмановских диаграмм. Изображенный слева стандартный фейнмановский пропагатор в виде прямой линии представляет целую матрицу из бесконечных сумм конечных зигзагов, показанную справа.

Читателя, который уже немного знаком с фейнмановскими диаграммами, может смутить  используемое здесь вертикальное упорядочение во времени. В квантовой теории поля обычно рисуют диаграммы, на которых временная переменная увеличивается слева направо. Этот выбор, при котором время течет снизу вверх, согласуется с принятым в теории  относительности, поскольку такое направление времени выбирается для большинства пространственно-временных диаграмм.

Большинство физиков пользуется формализмом «дираковских спиноров» (или 4-спиноров), в котором спинорные индексы отбрасываются. Вместо 2-спинора $\alpha_A$ они используют 4-спинор $(1-\gamma_5)\psi$  (называя его «левоспиральной частью дираковского электрона» или
как-нибудь в этом роде, вместо моей частицы «зиг») LINK8. Величина $\gamma_5$ представляет собой произведение
$$\gamma_5=-i\gamma_0\gamma_1\gamma_2\gamma_3$$
и обладает свойством антикоммутировать с каждым из элементов алгебры Клиффорда, при этом $\gamma_5^2=1$  Аналогично вместо $\beta_{A’}$ используется $(1+\gamma_5)\psi$ (правоспиральная часть).

Кто-то может заметить, что это всего лишь вопрос обозначений, и действительно можно переходить от 2-спинорного формализма к 4-спинорному и обратно. Зигзаг-представление определенно применимо (хотя и не всегда применяется) к любому формализму, однако к 2-спинорному формализму оно ближе, чем к 4-спинорному. Так реальны ли частицы «зиг» и «заг»? Можно сказатьчто они реальны в той же мере, в какой реален сам «дираковский электрон», — как в высшей степени полезное   идеализированное математическое описание одного из наиболее фундаментальных элементов Вселенной. Но есть ли это реальная «реальность»?

Комментарии (3):

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.