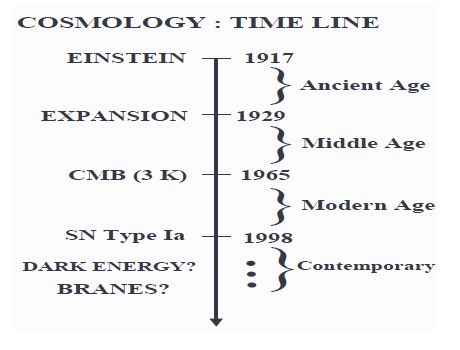
Опубликованные в 1998 году двумя независимыми группами результаты наблюдений SN Ia изменили наше представление о сегодняшнем состоянии Вселенной. Кратко говоря, анализ диаграммы Хаббла, описывающей наблюдаемую яркость этих объектов как функцию красного смещения, привела к неожиданному заключению, оказавшемуся поворотным пунктом в космологии: расширение Вселенной ускоряется, а не замедляется, как это считали в течение многих десятилетий. Неявно такие наблюдения подсказали, что объемная плотность энергии во Вселенной эффективно отталкивающая и предстает как некая новая компонента (дополнительная к темной массе), получившая название тёмной энергии (ТЕ) – новой формы энергии с отрицательным давлением.

Этот обзор является сокращенным переводом работы Alternative Dark Energy Models: An Overview.

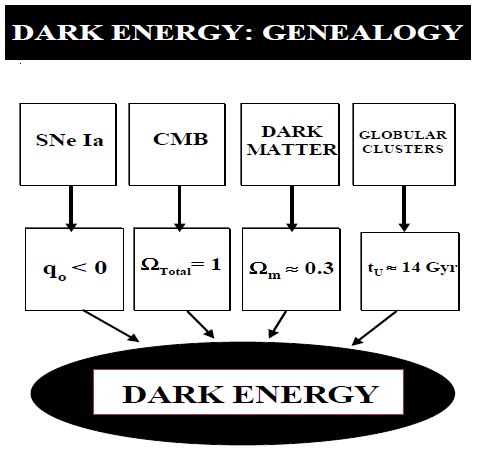
Существование дополнительной компоненты, заполняющей Вселенную, было также косвенно подтверждено с помощью независимых изучений

1. МКФ,
2. крупномасштабных структур,
3. возраста глобулярных кластеров или старых объектов с большим красным смещением,
4. X-ray данных по галактическим кластерам.

Действительно, угловые спектры мощности флуктуаций МКФ склоняются к значению ${{\Omega }_{T}}=1$, значению, впервые предсказанному теорией инфляции и также независимо необходимое для объяснения наблюдаемого спектра мощности крупномасштабных структур (КМС) и всеми перечисленными выше наблюдениями.

Разность ${{\Omega }_{DE}}={{\Omega }_{T}}-{{\Omega }_{m}}\sim 0.7$ и представляет плотность, соответствующую ТЕ компоненте. Такая картина была недавно подтверждена Wilkinson Microwave Anisotropy Probe и все эти ингредиенты укрепили модель, которую принято называть космологическим согласием (standard concordance model of cosmology). Хотя считается, что ТЕ изменила традиционный взгляд на Вселенную, отсутствие указаний со стороны теории элементарных частиц на ее происхождение дало толчок интенсивным дебатам и большому числу теоретических спекуляций. В частности космологическая константа (КК) $\Lambda $- один из старейших и наиболее естественных кандидатов. КК – простейший вариант с математической точки зрения. Но он не является единственной возможностью. $\Lambda $-член был первоначально введен Эйнштейном для получения статической модели мира. Этот член генерирует независящую от времени и пространственно однородную темную компоненту, которая может быть классически интерпретирована как субстанция с уравнением состояния ${{p}_{v}}=-{{\rho }_{v}}$.

В рамках квантовой теории поля присутствие $\Lambda $ обязано нулевым колебаниям всех частиц и полей, заполняющих Вселенную, которые проявляют себя как лембовский сдвиг или эффект Казимира. Однако с этим фаворитом имеется серьезная проблема, обычно называемая проблемой космологической константы. Проблема состоит в том, что настоящая верхняя граница $\left( {{\Lambda }_{0}}/8\pi G\sim {{10}^{-47}}Ge{{V}^{4}} \right)$ отличается от естественного теоретического ожидания $\left( m_{Pl}^{4}\sim {{10}^{71}}Ge{{V}^{4}} \right)$на почти 120 порядков. Эта головоломка рассматривается многими как величайший кризис современной физики (впервые проблема поставлена Зельдовичем еще в 1968 году) и висит как Дамоклов меч, занесенный над любой попыткой использовать КК для описания настоящей ускоренной стадии расширения Вселенной.

Сегодня в литературе имеется много других кандидатов для объяснения ТЕ. Среди них:
1. $\Lambda (t)$-член или распадающаяся плотность вакуумной энергии;
2. Реликтовое скалярное поле (SF) медленно скатывающееся вниз по своему потенциалу;
3. $X$- материя – дополнительная компонента, характеризующаяся уравнением состояния $p_X=w\rho_X,~~ -1 < w < 0;$
4. Аналог газа Чаплыгина, чье уравнение состояния $p=-A/{{\rho }^{\alpha }}$, где $A$-положительная константа, а $0\le \alpha \le 1$.

Список не является исчерпывающим, как может показаться на первый взгляд. Так как основное условие для ускорения Вселенной – доминирование компоненты с отрицательным давлением, то имеются и другие возможности, которые время от времени дебатируются в литературе. Отметим также, что модель, в которой доминирует КК (${{p}_{v}}=-{{\rho }_{v}}$) является предельным случаем $X$-материи с $w=-1$.

Три упомянутых выше кандидата – (скалярное поле, $X$-материя и газ Чаплыгина) могут обладать дополнительным физическим свойством: параметр $w$, входящий в уравнение состояния, может зависеть от КС $z$ \[w(z)=p/\rho \] Это означает, что много различных моделей может объяснять один и тот же набор наблюдательных данных. Следовательно, для того, чтобы улучшить наше понимание природы темной энергии, сегодня важной задачей является найти новые методы или восстановить старые, которые могут прямо или косвенно определить количество темной энергии во Вселенной и определить параметр уравнения состояния. Другими словами, с помощью информации о космическом ускорении при высоких и низких КС мы можем осуществить оптимальный выбор среди различных имеющихся теорий ТЕ, определяя $w$ и ее зависимость от времени.

В этом коротком обзоре мы представим упрощенную картину основных результатов и обсудим некоторые трудности, связанные с появлением на сцене ТЕ парадигмы. Так как варианты КК и скалярного поля (считающиеся лучшими кандидатами) были недавно осуждены в обзорах, мы сделаем ударение на оставшихся кандидатах. Далее мы ограничимся рассмотрением моделей, оперирующих с пространство-временем, описываемом FRW элементом длины $(c=1)$ \[d{{s}^{2}}=d{{t}^{2}}-{{R}^{2}}(t)\left[ d{{r}^{2}}+{{r}^{2}}\left( d{{\theta }^{2}}+{{\sin }^{2}}\theta d{{\varphi }^{2}} \right) \right]\] (1) Такая основа модели космического согласия есть прямое следствие последних МКФ результатов $\left( {{\Omega }_{tot}}=1 \right)$. Давайте теперь обсудим космическую динамику и некоторые следствия наблюдений для альтернативных кандидатов на роль ТЕ.
А. Зависящий от времени $\Lambda $-член.

Космология с распадающимся вакуумом или модели с зависящим от времени $\Lambda $-членом описываются в терминах смеси двух жидкостей: среда с распадающимся вакуумом (${{\rho }_{v}}(t)=\Lambda (t)/8\pi G,\ {{p}_{v}}=-{{\rho }_{v}}$) плюс жидкая среда, рассматривающаяся как продукт распада вакуума, характеризующаяся своей плотностью$\rho $ и своим давлением $p$. Идея зависящего от времени $\Lambda $- члена была впервые выдвинута Матвеем Бронштейном (1933). К сожалению, в течение многих десятилетий эта идея не встретила интереса.

Так было до середины 80-х. Полевые уравнения Эйнштейна (ПУЭ) и закон сохранения энергии (ЗСЭ) для $\Lambda (t)$ моделей имеют вид \[8\pi G\rho +\Lambda (t)=3{{\left( \frac{{\dot{R}}}{R} \right)}^{2}}\] (2) \[8\pi Gp-\Lambda (t)=-2\frac{{\ddot{R}}}{R}-\frac{{{{\dot{R}}}^{2}}}{{{R}^{2}}}\] (3)

\[\dot{\rho }+3(\rho +p)=-\frac{\dot{\Lambda }(t)}{8\pi G}\] (4) В обычном уравнении для изменения плотности появляется источник, связанный с зависимостью КК от времени) . Отметим, что уравнение (4) может быть переписано так, чтобы обеспечить выражение для скорости производства энтропии в этой модели \[T\frac{dS}{dt}=-\frac{\dot{\Lambda }{{R}^{3}}}{8\pi G}\] (5)

Отсюда видно, что $\Lambda $должно уменьшаться с течением времени, если энергия передается от распадающегося вакуума материальной компоненте $(\rho )$. Давайте теперь подчеркнем разницу между моделями с КК и распадающимся вакуумом. В последнем случае приводят обычно следующий аргумент: плотность вакуумной энергии зависит от времени потому, что она связана с другими полями материи во Вселенной. Благодаря расширению, мы можем предположить, что КК релаксирует к своему естественному значению $\Lambda =0$. В широком смысле, главная цель моделей с $\Lambda (t)$определить, как энергия, породившая инфляцию на ранних стадиях эволюции Вселенной и ускоряет в настоящее время связана с текущим значением $\Lambda $. Иногда предполагается, что плотность энергии распадающегося вакуума явно зависящая от времени убывающая функция.

Но в большинстве работ зависимость неявная на космологических временах, через масштабный фактор $\left( \Lambda \sim {{R}^{-2}} \right)$ или параметр Хаббла $\left( \Lambda \sim {{H}^{2}} \right)$ или даже в комбинации этих факторов. Все эти модели имеют одну и ту же ахиллесову пяту: не существует лагранжевого описания (ни какого-либо физического механизма) , включающего связь, которая описывает обмен энергией между распадающимся вакуумом и другими полями материи. Выражение, определяющее $\Lambda (t)$получается либо используя размерные аргументы, либо полностью ad hoc. Будучи феноменологическими, такие приближения могут тем не менее указать перспективный путь решения проблемы КК.

Одна из простейших возможностей для плотности распадающейся вакуумной энергии \[{{\rho }_{v}}=\frac{\Lambda (t)}{8\pi G}=\beta {{\rho }_{T}}\] где ${{\rho }_{v}}$ - плотность вакуумной энергии, а${{\rho }_{T}}={{\rho }_{v}}+\rho $ - полная плотность энергии и $\beta \in \left[ o,1 \right]$- безразмерный параметр порядка единицы. Комбинируя это условие с (2) можно получить $\Lambda (t)\sim {{H}^{2}}$, результат, который следует из размерных соображений.

В этом сценарии расширение может быть ускоренным, как этого требуют SN Ia наблюдения и правильно решается проблема возраста Вселенной при $z=0.$ С наблюдательной точки зрения, $\Lambda (t)CDM$ модели обладают интересной возможностью, которая отличает их от $\Lambda CDM$ моделей. Благодаря возможности адиабатического рождения фотонов, соотношение красное смещение-температура может быть слегка модифицировано. Для большого класса моделей \[T(z)={{T}_{0}}{{(1+z)}^{1-\beta }}\] (6) где ${{T}_{0}}$-температура МКФ при $z=0$. Это выражение подразумевает, что для данного КС $z$ температура Вселенной ниже, чем в стандартном сценарии с сохраняющимся числом фотонов.

B X-материя.

В космологическом сценарии Х-материя + холодная темная материя (иногда называемая XCDM параметризацией) обе жидкие компоненты сохраняются по отдельности. Уравнение состояния компоненты, соответствующей темной энергии, \[{{p}_{X}}=w(z){{\rho }_{X}}\]

Однако в отличие от моделей, связанных со скалярным полем, где $w(z)$ выводится в рамках рассматриваемого сценария, здесь он предполагается заданным a priori. Обычный выбор \[w(z)={{w}_{0}}{{(1+z)}^{n}}\] Модели с постоянным $w$ существенно проще, и их свободные параметры могут быть легко сконструированы, исходя из основных космологических данных. Модели с постоянным $w$ можно разбить на два класса: стандартные $$XCDM модели $(-1\le w<0)$ и обобщенные XCDM модели, называемые также фантомной энергией, допускающие $w<-1$ и тем самым нарушающие нуливое энергитическое условие.

Как мы видим, оценки ${{\Omega }_{m}}$ и $w$ совместимы для многих результатов, полученных существенно разными способами. Столь хорошее согласие не следует преувеличивать. Дело в том, что большинство космологических тестов высоко вырождены: т.е условия получаются на комбинации параметров, а не на каждый параметр в отдельности.

С. Газ чаплыгина.

Хорошо известно, что главное различие между CDM без давления и темной энергией состоит в том, что первая уплотняется на малых масштабах, в то время как темная энергия представляет собой гладкую (однородную) компоненту.

Такое свойство непосредственно связано с уравнениями состояния для обеих компонент. Недавно идея единого описания для CDM и ТЕ сценариев привлекла много внимания. Она может быть реализована с помощью газа Чаплыгина. Уравнение состояния для так называемого газа Чаплыгина (Cg) \[{{p}_{Cg}}=-A/{{\rho }^{\alpha }}\] (7) где $A$ и $\alpha $ - положительные константы. Уравнение (7) для $\alpha \ne 1$ обобщение исходного уравнения для газа Чаплыгина, в то время как случай $\alpha =0$ведет себя как $\Lambda CDM$модель.

Идея Единого описания ТМ и ТЕ = UDME сценария с помощью уравнения (7) инспирирована тем обстоятельством, что газ Чаплыгина дает естественную интерполяцию между режимами нерелятивистской материи и темной энергии с отрицательным давлением.

Так как в этом подходе имеется только одна темная компонента помимо барионов, фотонов и нейтрино, этот подход иногда называют Quartessence Cosmology.

III заключение

Исследования, связанные с темной энергией, сейчас в моде. Их лейтмотив – объяснение ускоренного расширения Вселенной, доказанное SNe и другими экспериментами при средних и высоких КС. Мы сфокусировали внимание на альтернативных кандидатах на роль ТЕ. Эта вездесущая компонента плюс ТМ составляют около 95% материи, заполняющей Вселенную.

Однако в отличие от ТМ темная энергия нужна для объяснения настоящей стадии расширения. Еу маленькая плотность и слабое взаимодействие, вероятно, исключают возможность ее идентификации в земных лабораториях. К несчастью, несмотря на то, что мы живем в золотой век эмпирической космологии, мы все еще не можем сделать выбор среди различных кандидатов. Это является сигналом о необходимости более точных наблюдений. Более точное определение космологических параметров останется центральной задачей ближайшего будущего.

Фундаментальная цель теоретиков пролить свет на природу ТЕ. Но не ясно, можно ли достичь этой цели, опираясь только на анализ уравнений состояния. Другая возможность – добавить некоторые гипотезы относительно происхождения ТЕ и анализировать следствия этих гипотез. Полезно отметить, что энергия этой релятивистской компоненты растет по мере ее адиабатического расширения. Макроскопически, энергия системы увеличивается за счет термодинамической работы, выполненной над системой (отрицательное давление). Это интригующее поведение находится в разительном контрасте с тем, что было бы для любой компоненты с положительным или нулевым давлением. Микроскопическое объяснение этого факта представляет большой интерес. Оно зависит от внутренней природы ТЕ и, конечно, будет иметь важные следствия для окончательной судьбы Вселенной. Кроме того, в настоящее время физическое сообщество охвачено возбуждением: хотя динамика Вселенной и сохраняет некоторые черты традиционной физической картины, новый невидимый актер (темная энергия) не был предсказан стандартной теорией элементарных частиц. И эта, ответственная за отталкивательную гравитацию субстанция, может глубоко изменить традиционный взгляд на пространство-время и материю.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.