Вселенная за пределами горизонта
Что лежит за пределами настоящего горизонта? Этот вопрос волновал меня с первых дней инфляции. Если мы видим только очень маленькую часть Вселенной, то какова большая картина. Это похоже на изменение восприятия Земли путешественником, покидающим ее на космическом корабле.
Теория плотностных возмущений в некоторой степени обеспечивает ключ к разгадке этой задачи. Согласно этой теории распределение галактик в пространстве определяется квантовыми толчками, которые испытало скалярное поле в течение инфляции. Это случайный процесс. Поэтому некоторые области одинакового размера содержат больше галактик, другие меньше. Млечный путь находится там, где мы, потому что скалярное поле в этом месте испытало небольшой толчок от истинного вакуума, поэтому скатилось с энергетической горы несколько позднее, чем соседние области. Это привело к небольшому увеличению плотности, которое позднее эволюционировало в нашу галактику. Аналогичные горбы привели к зарождению Андромеды и гигантского числа других галактик как внутри нашего горизонта, так и за его пределами. Такое описание образования структур предполагает, что удаленные части Вселенной выглядят так же, как и окружающая нас часть. Но мне с самого начала казалась, что в этой картине отсутствует что-то важное.

Эффект квантовых толчков очень мал, так как они существенно слабее, чем силы, обязанные наклону энергетической горы, которые управляют движением скалярного поля вниз. Это объясняет, почему поля достигает дна повсюду за одно и тоже время, и генерируются только малые флуктуации плотности. Вопрос, который я задал себе, был таков: что происходит вблизи вершины горы, где наклон очень мал? Может быть там мы находимся во власти квантовых толчков, которые случайным образом толкают поле на тот или иной путь. В таком случае Вселенная, подвергнутая инфляции, может быть значительно более случайной, чем это кажется на первый взгляд.
Чтобы понять поведение скалярного поля вблизи вершины горы, используем политически некорректную, но уместную аналогию – слишком много выпивший Mr. Field. Он пытается сохранить вертикальное положение. Шаг влево и вправо для него абсолютно случаен. Он начинает прогулку на вершине горы. Так как шаг влево и вправо для него равновероятен, он продвигается медленно. Но после большого числа шагов он будет постоянно удаляться от вершины горы. В конце концов он попадет на более крутую часть горы, где неизбежно поскользнется, и остаток путешествия будет скользить по склону горы вниз.
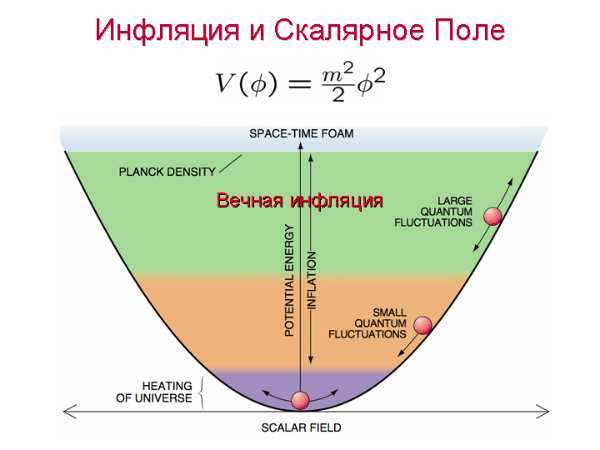
Скалярное поле в процессе инфляции ведет себя очень похожим образом. Поле бесцельно бродит вблизи вершины энергетической горы, пока не достигнет более крутой части. После этого оно скатывается вниз по направлению к концу инфляции. На плоской части, вблизи вершины изменение поля определяется квантовыми толчками и полностью случайно, в то время как скатывание по склону упорядоченно и предсказуемо, а квантовые толчки играют роль малого возмущения. Временной интервал между последовательными квантовыми толчками, грубо говоря, равен to удвоенному периоду инфляции (doubling time of inflation (DTI)). Это значит, что Mr. Field делает один шаг за DTI. И так как он делает много шагов в окрестности вершины горы, то фальшивому вакууму надо много DTI, чтобы распасться.
Конкретная последовательность шагов Mr. Field от вершины горы к подножью представляет одну возможную историю скалярного поля. Но квантовые толчки, испытываемые полем, отличаются в разных точках, поэтому истории скалярного поля будут также различны. Каждый квантовый толчок затрагивает малую область пространства. Размер этой области порядка расстояния, проходимого светом за время DTI. Будем называть его kickspan. Мы можем вообразить группу джентльменов, находящихся в тех же условиях, что и Mr. Field . Каждый из них представляет поле в некоторой точке пространства. Если две точки находятся внутри одного kickspan, они испытывают одинаковые квантовые толчки, так что соответствующие джентльмены шагают синхронно, как пара танцоров. Но точки быстро расходятся за счет инфляционного расширения Вселенной. Когда они расходятся на расстояние больше kickspan, их движения становятся независимыми. Когда это происходит, значения скалярного поля начинают постепенно расходится, в то время как расстояние между точками продолжает быстро увеличиваться за счет инфляции.
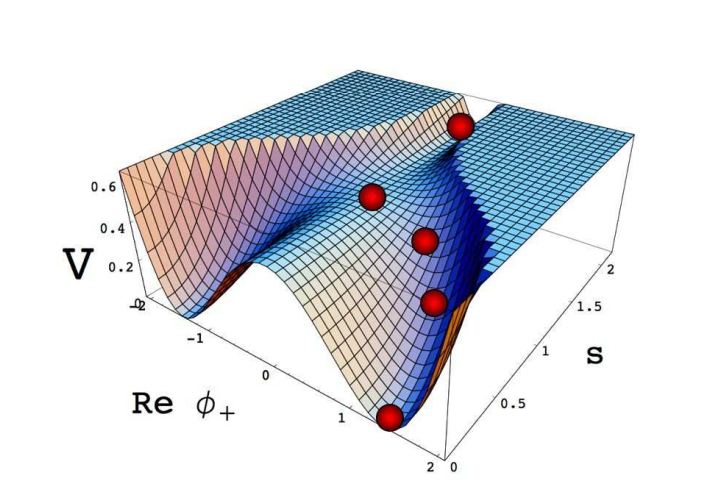
Малость плотностных возмущений в нашей наблюдаемой области говорит нам, что все точки этой области были внутри kickspan, когда скалярное поле значительно продвинулось по пути к подножью горы. Вот почему действие квантовых толчков было очень незначительно, и поле достигло дна повсюду в почти одно и тоже время. Но, если мы бы могли продвинуться на значительно большие расстояния, далеко за пределы нашего горизонта, мы бы увидели области, которые отделились от нашей компании, когда поле все еще было вблизи вершины. История скалярного поля в таких областях может существенно отличаться от нашей. Я б очень хотел знать, как выглядит Вселенная на таких гигантских масштабах.
Представим себе большую группу находящихся навеселе гуляк, стартующих с вершины горы. Каждый гуляка представляет отдаленную часть Вселенной, так что все они гуляют независимо. Если плоская часть горы составляет $N$ шагов, то типичный гуляка пройдет ее за $N^2$ шагов (Половина гуляк пройдет ее быстрее, вторая половина медленнее). Например, если дистанция составляет 10 шагов, то случайный гуляка пересечет ее за 100 шагов. Поэтому после первых 100 шагов половина компании достигнет конечной точки на дне горы, в то время как вторая будет радоваться прогулке. После следующих 100 шагов число гуляющих опять уменьшится вдвое. Так будет продолжаться, пока последний гуляка не скатится вниз.
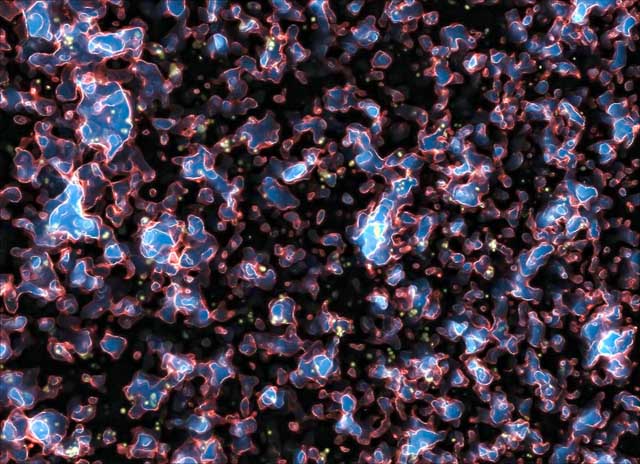
Но теперь имеется критическая разница между гуляками и инфляционными областями, которые они представляют. В то время как гуляки куролесили на вершине, соответствующие области подвергались инфляционному расширению. Поэтому число независимо эволюционирующих областей быстро множилось. Это происходило так, как если бы число гуляк также множилось. По мере того, как я размышлял об этом, картина понемногу приобретала форму.
Отрывок из книги А. Виленкина "Many Worlds in One: The Search for Other Universes"
Комментарии (1):
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.







Интересно, а могут ли всё это множество Вселенных влиять друг на друга, на подобии эффекта Ааронова-Бома?