Теория анизотропии МКФ нуждается в большом количестве информации о структуре ранней Вселенной. Поэтому она очень сложна. Однако, в силу этого же обстоятельства эта ветвь космологии обладает потенциальной (и отчасти уже реализованной) возможностью вычислить важнейшие космологические характеристики. Мы сконцентрируемся на концептуальном понимании того, как МКФ анизотропия может быть использована для вычисления космологических параметров.

Частичный перевод статьи The picture of our universe: A view from modern cosmology

А. Анизотропии МКФ

Модель Горячей Вселенной- общепризнанная модель ранней Вселенной. Согласно этой модели Вселенная стартовала в очень горячем и плотном состоянии. Она начала внезапно расширяться, и это расширение продолжается до настоящего времени. Невозможно наблюдать это расширение извне, и неверно думать, что Большой взрыв произошел в какой-то определенной точке. Большой взрыв произошел сразу везде.

Считается, что в течение первых долей секунды после БВ Вселенная прошла через кратковременную фазу экспоненциального расширения, называемую инфляцией. Барионы образовались в первую секунду, а ядра и легкие элементы (ядерный синтез) – когда Вселенной было несколько минут. Барионную материю называют обычной материей.

Ранняя Вселенная была достаточно горячей, чтобы материя оставалась ионизированной, поэтому Вселенная была заполнена нуклонами и свободными электронами. Плотность свободных электронов была так велика, что томсоновское рассеяние сделало Вселенную непрозрачной для электромагнитного излучения. Вселенная оставалась барионной плазмой 300.000 лет, пока Вселенная, расширяясь, не остыла до $3000\,K$.

Эта температура была достаточно низкой для образования нейтрального водорода. Этот процесс получил название рекомбинации. При этом плотность свободных электронов понизилась настолько, что средняя длина свободного пробега фотонов стала равна или больше текущего размера Вселенной. Свет стал распространяться свободно. Освобожденный в процессе рекомбинации свет к настоящему времени остыл до $2.73\,K.$ Этот свет мы наблюдаем сегодня как МКФ. Мы видим его пришедшим с некоторой сферической оболочки, называемой поверхностью последнего рассеяния. Эта оболочка имеет конечную толщину, потому что рекомбинация проходила конечное время.

Сегодня на очень больших масштабах Вселенная однородна. Однако, как это доказывается нашим собственным существованием, неоднородности существуют вплоть до масштабов порядка $100\,Mpc.$ Теории образования структур, которые мы наблюдаем сегодня, требуют, чтобы зародыши этих структур являлись неоднородностями плотности материи в ранней Вселенной. Эти неоднородности должны оставить следы в МКФ.

 Эти следы проявляются в форме температурной анизотропии МКФ. Поэтому, для того чтобы объяснить Вселенную, в которой мы живем, мы должны изучать неоднородности МКФ. Эти неоднородности должны быть связаны с масштабом наблюдаемых сегодня структур. В 1992 году спутник COBE обнаружил температурные флуктуации $\delta T$в МКФ,$\delta T/T\sim {{10}^{-5}}$ на ${{7}^{0}}$ угловом масштабе. Анизотропии, детектируемые COBE, рассматривались как крупномасштабные флуктуации, вызванные неоднородностями, генерируемыми при образовании Вселенной. 

Однако, недавние наблюдения обнаружили мелкомасштабные анизотропии, которые соответствуют физическому масштабу наблюдаемых сегодня структур. Считается, что эти анизотропии являются результатом квантовых флуктуаций в плотности. Они существовали до инфляции, но были чудовищно усилены в период инфляции. Эти усиленные флуктуации и стали внутренними возмущениями плотности, семенами нынешних структурных образований. 

 Мелкомасштабные анизотропии в МКФ могут быть разделены на две категории: первичные и вторичные. Первичные анизотропии возникли в период рекомбинации и «впечатаны» в МКФ (сохраняются в МКФ после того как фотоны покинули поверхность последнего рассеяния (ППР)). Вторичные анизотропии возникают в процессе рассеяния фотонов на их пути от ППР до наблюдателя. В этом обзоре мы будем интересоваться только первичными анизотропиями. Существует три источника первичной анизотропии МКФ: Suchs-Wolfe, внутренние (адиабатические) возмущения, эффект Доплера.

Для первичных анизотропий доминирующим является эффект Suchs-Wolfe. Он состоит в следующем. Флуктуации плотности на ППР приводят к возмущениям в гравитационном потенциале $\delta \Phi.$ Эти возмущения вызывают гравитационное красное смещение фотонов, покидающих ППР, когда они выбираются из потенциальных ям. Этот эффект приводит к  $$\frac{\delta T}{T}=\frac{\delta \Phi}{c^2}.$$ 

Эти же возмущения в гравитационном потенциале вызывают растяжение временного интервала на ППР, поэтому эти фотоны появляются из более молодой (ранней) и более горячей Вселенной. Этот эффект приводит к  $$\frac{\delta T}{T}=-2\frac{\delta \Phi}{3c^2}.$$

Комбинация этих двух эффектов и дает  эффект Suchs-Wolfe: \begin{equation}\frac{\delta T}T=\frac{\delta \Phi }{3c^2}.\end{equation}

На промежуточных масштабах основной эффект обязан адиабатическим возмущениям. Рекомбинация возникает позже в тех областях, где плотность больше, поэтому фотоны, испускаемые областями с повышенной плотностью, испытывают меньшее красное смещение, обязанное универсальному расширению  и потому оказываются более горячими. Наблюдаемая температурная анизотропия, обязанная этому процессу \begin{equation}\left(\frac{\delta T}T\right)_{obs}=-\frac{\delta z}{1+z}=\frac{\delta \rho }\rho.\end{equation}

Наконец, на самых маленьких масштабах важным становится эффект Доплера. Он возникает потому, что на ППР фотоны рассеиваются в движущейся плазме. Температурная анизотропия, соответствующая этому эффекту, \begin{equation}\frac{\delta T}T=\frac{\delta \overrightarrow{v}\cdot \widehat{r}}c, \end{equation} Где единичный вектор $\widehat{r}$ направлен по направлению взгляда, а $\overrightarrow{v}-$ характерная скорость материала рассеивающей среды.

 B. Акустические пики и космологические параметры

Ранняя Вселенная представляла собой плазму фотонов и барионов, которую можно рассматривать как единую жидкость. Барионы попадали в потенциальные ямы, создаваемые флуктуациями плотности, и сжимались. Это сжатие приводило к нагреву плазмы и, как следствие, к увеличению радиационного давления фотонов, направленного наружу. В конце концов, радиационное давление остановит сжатие и вызовет расширение плазмы. Охлаждение плазмы при расширении приведет к уменьшению радиационного давления. Гравитация опять начнет доминировать, приводя к повторному сжатию. Конкуренция между гравитацией и давлением излучения приводит к продольным (акустическим) осцилляциям в фотон-барионной жидкости. Когда материя и излучение «развязываются» в момент рекомбинации, картина акустических колебаний остается вмороженной в МКФ. Сегодня мы детектируем доказательство существования звуковых волн (областей пониженной и повышенной плотности) в форме первичной анизотропии МКФ.

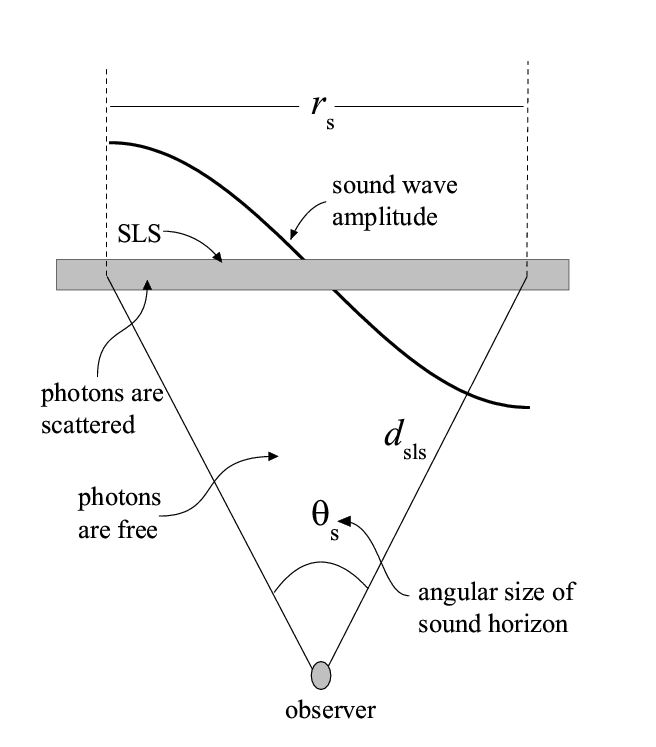
Рис. 1. Поверхность последнего рассеяния (ППР), фундаментальная акустическая мода и звуковой горизонт. Фотоны МКФ испытывая томсоновское рассеяние в ранней Вселенной и акустические осцилляции, которые несут отпечаток рекомбинации.

Хорошо известно, что любая звуковая волна, независимо от того, насколько она сложна, может быть представлена в виде суперпозиции мод с различными волновыми числами $k$, $k\propto 1/\lambda $. Каждой моде $\lambda$ отвечает определенный угловой размер $\theta $ на небе. Следовательно, для того чтобы облегчить сравнение теории с экспериментом, вместо разложения Фурье для акустических колебаний (в терминах синусов и косинусов) следует использовать угловое (мультипольное) разложение в терминах полиномов Лежандра  ${{P}_{l}}(\cos \theta )$. Порядок полинома $l$играет ту же роль, что и $k$в разложении Фурье. Для $l\ge 2$ полиномы Лежандра –осциллирующие функции на интервале $\left[ 1,-1 \right]$. Число осцилляций увеличивается по мере роста $l$. Следовательно, \begin{equation}\ell \propto 1/\theta .\end{equation}

Экспериментально, температурные флуктуации могут быть количественно проанализированы с помощью парных измерений в направлениях $\widehat{n}$  и $\widehat{n^{\prime }}$ разделены на угол $\theta $, так что $\widehat{n}\cdot \widehat{n^{\prime }}=\cos\theta .$ Усредняя по всем таким парам (в предположении, что флуктуации гауссовы), мы получим двухточечную корреляционную функцию $C(\theta )$, которая может быть представлена в терминах мультипольного разложения \begin{equation}\left\langle \delta T(\widehat{n})\cdot \delta T(\widehat{n^{\prime }})\right\rangle \equiv C(\theta )=\sum\limits_\ell \frac{(2\ell +1)}{4\pi }C_\ell P_\ell (\cos \theta ), \end{equation} где $C_\ell $-коэффициенты мультипольного разложения. 

Как мы говорили, анализ температурных флуктуаций позволяет выяснить структуру продольных колебаний. Мода с наибольшей длиной волны соответствует наибольшему угловому размеру первичной анизотропии. Эта фундаментальная мода была детектирована первой. Сейчас имеются серьезные доказательства того, что вторая и третья моды также были детектированы. Расстояние ${{r}_{s}}$, которое звуковая волна может пройти за время, прошедшее до рекомбинации, называется   звуковым горизонтом. Звуковой горизонт фиксируется (или фиксирует) физическим масштабом на ППР. Размер звукового горизонта зависит от значений физических параметров.  Расстояние до поверхности последнего рассеяния ${{d}_{sls}}$также зависит от космологических параметров. Вместе они определяют угловой размер звукового горизонта \begin{equation}\theta _s\approx \frac{r_s}{d_{sls}}.\end{equation}

Так, например, угловой размер Юпитера зависит как от его размера, так и от расстояния до него. Анализ температурных анизотропий позволяет определить ${{\theta }_{s}}$. Варьируя космологические параметры, входящие в ${{r}_{s}},{{d}_{sls}}$ мы добиваемся наилучшего согласия с наблюдением для ${{\theta }_{s}}$, и тем самым фиксируем космологические параметры. 

Мы можем оценить величину звукового горизонта как путь проходимый звуком от момента $t=0$до момента рекомбинации ${{t}_{*}}$\begin{equation}r_s(z_{*};\Omega_b,\Omega _r)\approx \int_0^{t_{*}}c_sdt,\end{equation} где $z_{*}$ времени рекомбинации ($z_{*}\approx 1100$), $\Omega _r$, $c_s$-скорость звука в фотон-барионной среде \begin{equation}c_s\approx c\left[ 3\left( 1+3\Omega _b/4\Omega _r\right) \right] ^{-1/2}.\end{equation} 

$dt$ определяется из первого уравнения Фридмана $${\left( {\frac{{\dot a}}{a}} \right)^2} = \frac{{8\pi G}}{{3{c^2}}}\rho  - \frac{{k{c^2}}}{{{a^2}}}$$ ($k-$ пространственная кривизна). 

 Плотность энергии излучения ведет себя как $\rho_r\propto a^{-4}$, поэтому добавляя излучение в уравнение Фридмана и учитывая все остальные компоненты, получим \begin{equation}\left( \frac{da}{dt}\right) ^2=H_0^2\left[ \Omega _{r,0}\left( \frac{a_0}a\right) ^2+\Omega _{m,0}\frac{a_0}a+\Omega _{k,0}+\Omega _{\Lambda ,0}\left(\frac a{a_0}\right) ^2\right] .\end{equation} Используя $\frac{a_0}{a} = 1 + z$ и $\Omega _r+\Omega _m+\Omega _\Lambda +\Omega_k=1$, получим \begin{equation}dt=H_0^{-1}(1+z)^{-1}\left\{ (1+z)^2(1+\Omega _{m,0}z)+z(z+2)\left[(1+z)^2\Omega _{r,0}-\Omega _{\Lambda ,0}\right] \right\} ^{-1/2}dz.\end{equation}

Расстояние до ППР, соответствующее ее угловому размеру, определяется величиной называемой расстоянием углового диаметра. Оно просто связано с расстоянием светимости $d$, которое входит в \begin{equation}d=\frac{c(1+z)}{H_0|\Omega_{k,0}|^{1/2}}\text{sinn}\left\{|\Omega_{k,0}|^{1/2}\int\nolimits_0^z\left[ (1+z^{\prime })^2(1+\Omega_{m,0}z^{\prime })-z^{\prime }(z^{\prime }+2)\Omega _{\Lambda ,0}\right]^{-1/2}dz^{\prime }\right\} ,\end{equation} где  sinn$(x)$ есть $\sinh (x)$ для $k<0$, $\sin (x)$для$k>0$, и если $k=0$ то не sinn ни $|\Omega _{k,0}|$ не входит в выражение. 

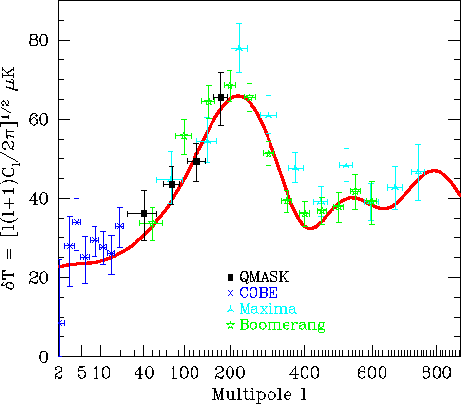
Рис. 2. Угловой спектр флюктуаций реликтового излучения по данным экспериментов BOOMERanG, MAXIMA и QMASK. Положение первого пика на $l = 200$ соответствует плоской геометрии пространственных сечений Вселенной (параметр $\Omega = 1 \pm 0,1$).

Расстояние до ППР, имеет вид \begin{equation}d_{sls}=\frac{d(z_{*};\Omega _m,\Omega _\Lambda )}{(1+z_{*})^2}.\end{equation} 

Положение первого акустического пика задается $\ell \approx d_{sls}/r_s $ и очень чувствительна к кривизне Вселенной $\Omega_k.$ 

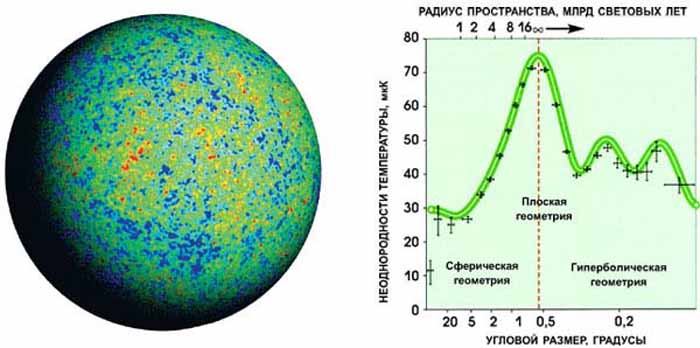
Рис. 3. Слева: флуктуации фона реликтового излучения, по данным спутника WMAP. Неоднородности, показанные цветом, составляют всего несколько стотысячных градуса, но они привели к новой картине мира. Справа: Угловой спектр флюктуаций реликтового излучения. Именно по этим колебаниям делают вывод о плоскостности или кривизне мира, о которых писал А. А. Фридман.

Чтобы лучше «почувствовать» результат, давайте рассмотрим упрощенную версию: предскажем первый акустический пик для случая плоской Вселенной. В основном порядке скорость звука $c_s=c/\sqrt{3}.$  Предположит также, что в эпоху рекомбинации во Вселенной доминировала материя. В этих предположениях получим \begin{equation}r_s=\frac{c_s}{H_0\sqrt{\Omega _m}}\int_{z_{*}}^\infty (1+z)^{-5/2}dz,\end{equation} Что дает \begin{equation}r_s=\frac{2c_s}{3H_0\sqrt{\Omega_m}}(1+z_{*})^{-3/2}.\end{equation} Расстояние до ППР в нашей модели будет зависеть от ${{\Omega }_{m}},{{\Omega }_{\Lambda}}$.  И следовательно  для радиальной координаты ППР получим, ${{r}_{sls}}$, \begin{equation}r_{sls}=\frac c{H_0}\int_0^{z_{*}}\left[ \Omega _m(1+z)^3+\Omega _\Lambda\right] ^{-1/2}dz,\end{equation}  используем биноминальное разложение для подынтегрального выражения  $\Omega _m^{-1/2}(1+z)^{-3/2}-(\Omega_\Lambda /2\Omega _m^{3/2})(1+z)^{-9/2}.$ Теперь интеграл можно вычислить. Учитывая что $d_{sls}=r_{sls}/(1+z_{*})$ получим \begin{equation}d_{sls}=\frac{2c}{7H_0(1+z_{*})}\left\{ 7\Omega _m^{-1/2}-2\Omega _\Lambda\Omega _m^{-3/2}+O[(1+z_{*})^{-1/2}]\right\} .\end{equation} 

Используя ${{\Omega }_{\Lambda }}=1-{{\Omega }_{m}}$и пренебрегая членами высших порядков, получим \begin{equation}d_{sls}\approx \frac{2c\Omega _m^{-1/2}}{7H_0(1+z_{*})}\left\{ 9-2\Omega_m^3\right\} .\end{equation} Комбинируя выражение для $r_s$ и $d_sls$ получим  \begin{equation}d_{sls}\approx\frac{2c\Omega_m^{-1/2}}{7H_0(1+z_{*})}\left\{9-2\Omega_m^3\right\} .\end{equation} Тогда для первого акустического пика \begin{equation}\ell \approx \frac{d_{sls}}{r_s}\approx 0.74\sqrt{(1+z_{*})}\left\{9-2\Omega _m^3\right\} \approx 221.\end{equation}  Этот результат согласуется с более аккуратными вычислениями, согласно которым \begin{equation}\ell \approx 200/\sqrt{1-\Omega _k},\end{equation}  где в нашем приближении ${{\Omega }_{k}}=0$. Это соотношение подразумевает, что обнаруженное в наблюдениях значение $l\approx 200$соответствует плоской Вселенной. BOOMERANGобнаружил $l\approx 197\pm 6$, aMAXIMA-1 -$l\approx 200$. 

Экспериментальные результаты представляются  в виде графика спектра мощности ${{\left( \delta {{T}_{l}} \right)}^{2}}$ (или корня из этой величины), задаваемой соотношением:

      \[{{\left( \delta {{T}_{l}} \right)}^{2}}=\frac{l(l+1)}{2\pi }{{C}_{l}}\]

Спектр мощности может быть быстро вычислен в рамках определенной космологической модели, используя стандартные программы.

В то время как положение первого пика позволяет зафиксировать ${{\Omega }_{k}}$, другие особенности спектра мощности помогают определить барионную плотность. Барионы действуют на спектр мощности несколькими способами. Так, например, увеличение барионной плотности приводит к усилению нечетных пиков и росту затухания высоких мультиполей.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.