Хаотическая инфляция
Одним из главных желаний физиков является построение теории, которая бы естественным образом предсказывала наблюдаемые значения всех параметров фундаментальных частиц. Хочется верить, что правильная теория, описывающая наш мир, должна быть красивой и простой.
Перевод замечательной статьи А.Д. Линде Inflation, Quantum Cosmology and the Anthropic Principle
Однако большинство параметров элементарных частиц больше похожи на набор случайных чисел, чем на проявления некой скрытой гармонии природы. Например, масса электрона в тысячу раз меньше массы протона, который на два порядка легче W-бозона, масса которого на 17 порядков меньше фундаментальной планковской Между тем, уже достаточно давно было отмечено, что небольшое изменение (в 2-3 раза) массы электрона, постоянной тонкой структуры $\alpha_e$, константы сильного взаимодействия $\alpha_s$ или постоянной тяготения $G= M_p^{-2}$ привело бы к тому, что жизнь того типа, который мы знаем, никогда не смогла бы возникнуть. Добавление или изъятие хотя бы одного из пространственных измерений сделало бы невозможным существование планетных систем. Действительно, при размерности пространства-времени $d > 4$ сила гравитационного взаимодействия падает быстрее, чем $r^{-2},$ а при $d < 4$ общая теория относительности утверждает полное отсутствие такой силы. Это говорит о невозможности существования стабильных планетных систем при $d\not = 4.$ Более того, для существования известной нам жизни необходимо, чтобы вселенная была достаточно большой, плоской, однородной и изотропной. Все это, а также некоторой количество иных аргументов, привело к формулировке так называемого антропного принципа(Barrow and Tipler, 1986; Rozental, 1988; Rees, 2000) В соответствии с ним, мы видим вселенную такой, какая она есть, потому, что только в такой вселенной могла возникнуть жизнь и, соответственно, мы сами.
До недавнего времени многие ученые предпочитали не упоминать антропный принцип в своих работах. Типичное отношение к нему было выражено в книге ``Ранняя Вселенная'' Колбом и Тернером (Kolb и Turner): `` Одному из авторов неясно, как такая невразумительная идея, как антропная, могла быть возвышена до уровня принципа'' (Kolb, 1990).
Такое скептическое отношение достаточно оправданно. Гораздо лучше найти простое физическое решение проблемы, чем спекулировать на тему того, что мы можем жить только в такой вселенной, в которой эта проблема отсутствует. Всегда есть риск того, что антропный принцип не решит проблему, а лишь послужит отговоркой.
С другой стороны, этот принцип может помочь нам осознать, что самые сложные и фундаментальные проблемы могут быть почти тривиальными, если взглянуть на них с другой точки зрения. Вместо того, чтоб отвергать или некритично принимать его, необходимо использовать более осторожный подход и решать, может ли он быть полезным в каждом конкретном случае.
Существуют две главные разновидности этого принципа: слабый и сильный антропный принципы Слабый антропный принцип просто говорит, что если вселенная состоит из частей с различными свойствами, то мы будем жить там, где наша жизнь возможна. Это кажется достаточно очевидным, неясно только, существуют ли во вселенной эти различающиеся области. Если нет, то любое обсуждение изменений массы электрона и постоянных взаимодействий совершенно бессмысленно.
Сильный антропный принцип утверждает, что вселенная должна была быть создана такой, чтоб в ней стало возможно наше существование. На первый взгляд, это утверждение не может быть справедливым, потому как человечество, возникшее спустя $10^{10}$ лет после установления базовых свойств нашей вселенной, никак не могло повлиять на ее структуру и на свойства элементарных частиц в ней.
Ученые часто связывали антропный принцип с идеей многократного (до достижения желаемых результатов) создания вселенной. Было неясно, кто этим занимался, и почему было необходимо создать вселенную, пригодную для нашего обитания. Более того, было бы гораздо проще создать подходящие для нас условия в малой окрестности солнечной системы, чем во всей вселенной. Зачем было усложнять задачу?
К счастью, большинство проблем, связанных с антропным принципом, были решены (Linde, 1983a,1984b,1986a) вскоре после создания инфляционной космологии. Потому далее мы напомним ее основные принципы.
Хаотическая инфляция
Инфляционная теория формулировалась во множестве вариантов, начиная с моделей, основанных на квантовой гравитации (Starobinsky, 1980) и теории высокотемпературных фазовых переходов со сверхохлаждением (supercooling) и экспоненциальным расширением в состоянии ложного вакуума (Guth, 1981; Linde, 1982a; Albrecht and Steinhardt, 1982). Однако, с появлением сценария хаотической инфляции (Linde, 1983b) было понято, что основные принципы инфляции очень просты, и что для нее вовсе не обязательны термодинамическое равновесие, сверхохлаждение и расширение в состоянии ложного вакуума.
Для объяснения основной идеи хаотической инфляции рассмотрим простейшую модель скалярного поля $\phi$ с массой $m$ и плотностью потенциальной энергии $V(\phi) = {m^2\over 2} \phi^2$ (см. рис. 1). Так как эта функция имеет минимум при $\phi = 0,$ можно было бы ожидать осцилляций скалярного поля $\phi$ вблизи этого минимума. Это действительно имеет место, если вселенная не расширяется. Однако, можно показать, что в быстро расширяющейся вселенной скалярное поле скатывается вниз очень медленно, подобно шарику в вязкой жидкости, причем эффективная вязкость оказывается пропорциональной скорости расширения.
Эволюция однородного скалярного поля в нашей модели описывается двумя уравнениями - уравнением для поля
$$\ddot\phi + 3H\dot\phi = -m^2\phi ,$$
и уравнением Эйнштейна
$$H^2 +{k\over a^2} ={8\pi \over 3M_p^2}\, \left( {1\over 2}\dot \phi^2+V(\phi) \right).$$
Здесь $H = \dot a/a $ - постоянная Хаббла для вселенной с масштабным фактором $a(t)$ (размер вселенной), $k = -1, 0, 1$ соответственно для открытой, плоской и закрытой моделей, $M_p$- планковская масса, $M_p^{-2} = G,$ где $G$ - гравитационная постоянная. Первое уравнение похоже на уравнение движения гармонического осциллятора, где вместо $x(t)$ мы имеем $\phi(t)$. Член $3H\dot\phi$ аналогичен описывающему вязкость в уравнении для гармонического осциллятора.
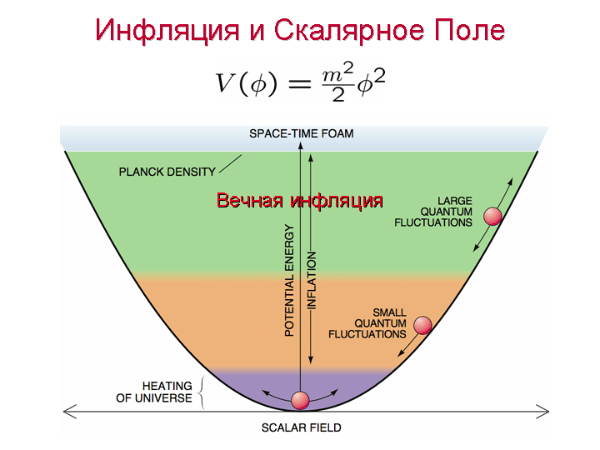
Рис. 1. Движение скалярного поля в теории с $V(\phi) = {m^2\over 2} \phi^2.$ Возможны несколько различных режимов в зависимости от величины поля $\phi$ Если плотность потенциальной энергии поля превышает планковское значение $\rho \sim M_p^4 \sim 10^{94}$ г/см$^3$, квантовые флуктуации пространства-времени настолько сильны, что их уже нельзя описать в обычных терминах. Это состояние называется пространственно-временной пеной. На чуть меньших энергиях (область A: $m M_p^3 < V(\phi) < M_p^4$) квантовые флуктуации пространства-времени малы, но флуктуации скалярного поля $\phi$ могут быть значительными. Скачки скалярного поля, вызванные квантовыми флуктуациями, приводят к вечному самовоспроизведению инфляционной вселенной (что мы обсудим ниже). При еще меньших величинах $V(\phi)$ (область B:$m^2 M_p^2 < V(\phi) < m M_p^3$) флуктуации скалярного поля малы, оно медленно скатывается подобно шарику в вязкой жидкости. Инфляция имеет место как в области A, так и в области B. Наконец, вблизи минимума $V(\phi)$ (область C) скалярное поле быстро осциллирует, рождая пары элементарных частиц, и вселенная становится горячей.
Если скалярное поле $\phi$ изначально было большим, постоянная Хаббла $H$ также была велика, в соответствии со вторым уравнением. Это означает, что вязкий член был очень большим, и скалярное поле двигалось очень медленно, подобно шарику в вязкой жидкости. Потому на этой стадии плотность энергии скалярного поля, в отличие от подобной величины для обычной материи, оставалась практически постоянной, и расширение вселенной продолжалось с гораздо большей скоростью, чем в старой космологической теории. Благодаря быстрому росту размеров вселенной и медленности движения поля $\phi,$ вскоре после начала данной стадии мы имеем $\ddot\phi \ll 3H\dot\phi,$ $H^2 \gg {k\over a^2},$ $ \dot \phi^2\ll m^2\phi^2,$ так что можно упростить систему уравнений:
$$ 3{\dot a \over a}\dot\phi = -{m^2\phi} \ , $$ $$H ={\dot a \over a} ={2 m\phi\over M_p}\, \sqrt { \pi \over 3} \ .$$
Последнее уравнение показывает, что размер вселенной $a(t)$ на данной стадии растет примерно как $e^{Ht},$ где $H = {2 m\phi\over M_p}\, \sqrt { \pi \over 3}.$
Эта стадия экспоненциально-быстрого расширения называется инфляцией. В реалистичных версиях инфляционной теории ее длительность может быть достаточно малой, вплоть до $10^{-35}$ секунд. Как только поле $\phi$ становится достаточно малым, вязкость также уменьшается, инфляция кончается, и скалярное поле начинает осциллировать вблизи минимума $V(\phi).$ Как любое быстро осциллирующее классическое поле, оно теряет энергию за счет рождения пар частиц. Эти частицы, взаимодействуя между собой, приходят в тепловое равновесие с некой температурой $T$. С этого момента соответствующая часть вселенной может быть описана стандартной теорией горячей вселенной.
Главное отличие инфляционной теории от старой космологии становится очевидным, если посчитать размер типичной инфляционной области в конце инфляции. Даже если начальный размер инфляционной вселенной был очень мал (порядка планковского длины $l_P \sim 10^{-33}$ см.), после $10^{-35}$ секунды инфляции вселенная достигает огромных размеров - $l \sim 10^{10^{12}}$ см. Это приводит к тому, что вселенная становится практически плоской и однородной на больших масштабах, так как все неоднородности растягиваются в $10^{10^{12}}$ раз.
Этот фактор является модельно-зависимым, однако во всех реалистичных моделях вселенная после инфляции оказывается на много порядков больше масштаба той части вселенной, которую мы можем видеть ($l \sim 10^{28}$ cm). Это сразу же решает большинство проблем классической космологии (Linde, 1990a).
Рассмотрим вселенную, изначально состоящую из многих областей со случайным образом распределенным скалярным полем $\phi$ (или же ансамбль вселенных с различными величинами поля). В тех частях, где скалярное поле слишком мало, инфляция никогда не начинается, потому они не вносят существенного вклада в объем вселенной. Основную же ее часть занимают те области, в которых скалярное поле изначально было большим. Инфляция таких областей формирует огромные "острова" в первичном хаосе, размер каждого такого "острова" существенно превышает размер наблюдаемой части вселенной. Именно поэтому я называю этот сценарий хаотической инфляцией
Есть существенное отличие данного сценария от старой идеи создания всей вселенной в некий момент времени (Большой Взрыв) практически однородной и нагретой до бесконечно больших температур. В новой модели более не требуются условия изначальной однородности и термодинамического равновесия. Каждая часть вселенной может иметь сингулярное начало (см. в работе (Borde et al, 2001) обсуждение современного состояния вопроса). Однако, в контексте хаотической инфляции это не означает, что вся вселенная как целое возникла из сингулярности. Различные части вселенной могли возникать в разные моменты времени, и потом разрастаться до размеров, значительно превышающих размер вселенной. Наличие начальной сингулярности (или сингулярностей) не означает, что вселенная была создана как целое в результате единственного Большого взрыва. Это означает, что бы более не вправе говорить, что вся вселенная родилась в некий момент времени $t=0$, до которого ее не существовало. Это справедливо для всех вариантов теории хаотической инфляции, даже если не принимать во внимание процесс самовоспроизведения вселенной, обсуждающийся в разделе 4.
Возможность того, что наша однородная часть вселенной возникла из начального хаотического состояния, имеет важное значение для антропного принципа. До сих пор мы рассматривали простейшую инфляционную модель с всего одним скалярным полем. Реалистичные модели элементарных частиц, однако, вводят множество других скалярных полей. Например, в соответствии со стандартной теорией электрослабого взаимодействия, массы всех элементарных частиц зависят от величины хиггсовского скалярного поля $\varphi$ в нашей вселенной. Эта величина определяется положением минимума эффективного потенциала $V(\varphi).$ В простейших моделях $V(\varphi)$ имеет только один минимум. Однако в общем случае этот потенциал может иметь множество различных минимумов. Так, в простейшей суперсимметричной теории, объединяющей слабое, сильное и электромагнитное взаимодействия, эффективный потенциал имеет несколько различных минимумов равной глубины по отношению к двум скалярным полям, $\Phi$ и $\varphi.$ Если эти скалярные поля скатываются в различные минимумы в разных частях вселенной (этот процесс называют спонтанным нарушением симметрии), массы элементарных частиц и законы взаимодействий в них будут различными. Каждая из этих частей может стать экспоненциально большой в результате инфляции. В некоторых из этих частей не будет разницы между сильным, слабым и электромагнитным взаимодействиями, и жизнь нашего типа будет невозможна. Другие же части будут похожи на ту, в которой живем мы (Linde, 1983c).
Это значит, что даже если мы и найдем последнюю Теорию Всего (TOE, Theory of Everything), мы все равно будем не в состоянии однозначно предсказать свойства элементарных частиц в нашей вселенной; вселенная может состоять из различных экспоненциально больших частей с различными свойствами элементарны частиц. Это - важный шаг на пути к доказательству антропного принципа. Следующий же шаг может быть сделан, если мы примем во внимание квантовые флуктуации в процессе инфляции.
Квантовые флуктуации на инфляционной стадии
В соответствии с квантовой теорией поля, пустое пространство не вполне пусто. Оно наполнено квантовыми флуктуациями всех видов физических полей. Длины волн всех квантовых флуктуаций скалярного поля $\phi$ в ходе инфляции растут экспоненциально. Как только длина волны какой-либо флуктуации становится большей, чем $H^{-1},$ она прекращает осциллировать и ее амплитуда замораживается на некой ненулевой величине $\delta\phi (x)$ из-за большого вязкого члена $3H\dot{\phi}$ в уравнении движения скалярного поля. Амплитуда этой флуктуации в дальнейшем остается практически неизменной, тогда как ее длина волны экспоненциально растет. Таким образом, проявления такой "замороженной" флуктуации равносильны проявлениям классического поля $\delta\phi (x),$ рожденного квантовыми флуктуациями.
Так как в вакууме содержатся флуктуации всех длин волн, инфляция ведет к непрерывному рождению новых возмущений классического поля с длинами волн, большими $H^{-1}$. Средняя амплитуда возмущений, рожденных за интервал времени $H^{-1}$ (за это время вселенная расширяется в $e$ раз) дается выражением $ |\delta\phi(x)| \approx \frac{H}{2\pi}$ (Vilenkin and Ford, 1982; Linde, 1982c).

Эти квантовые флуктуации ответственны за формирование галактик(Mukhanov and Chibisov, 1981; Hawking, 1982; Starobinsky, 1982; Guth and Pi, 1982; Bardeen et al, 1983). Однако если в ходе инфляции постоянная Хаббла достаточно велика, квантовые флуктуации скалярных полей могут приводить не только к формированию галактик, но также и к разделению вселенной на экспоненциально большие области с различными свойствами.
Для примера вновь рассмотрим простейшую суперсимметричную теорию, объединяющую слабое, сильное и электромагнитное взаимодействия. Различные минимумы эффективного потенциала в данной модели разделены расстоянием $\sim 10^{-3} M_p$. Амплитуды квантовых флуктуаций полей $\phi,$ $\Phi$ и $\varphi$ в начале инфляционной стадии могут достигать $10^{-1} M_p$. Это значит, что на начальных стадиях инфляции скалярные поля $\Phi$ и $\varphi$ могут свободно перепрыгивать из одного минимума потенциала в другой. Потому, даже если они изначально находились в одном и том же минимуме по всей вселенной, по окончании стадии хаотической инфляции вселенная окажется разделена на множество экспоненциально больших областей, соответствующих всем возможным минимумам эффективного потенциала.(Linde, 1983c, 1984b).
- Введение
- Хаотическая инфляция
- Квантовые флуктуации на инфляционной стадии
- Вечная хаотическая инфляция
- Дочерние вселенные
- От вселенной к Мультимиру
- Модель двойной вселенной и проблема космологической постоянной.
- Космологическая постоянная, темная энергия и антропный принцип.
- Проблема вычисления вероятностей
- Имеет ли значение сознание?
- Почему математика столь эффективна?
- Почему именно квантовая?
- Использованная литература
Нет комментариев.
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.






