Энтропийное ускоренное расширение Вселенной
Наиболее важное наблюдение в космологии после Хаббла – открытие ускоренного расширения Вселенной. Огромное число последующих наблюдений подтвердили этот факт. Однако, имелось много попыток опровергнуть заключение о космическом ускорении. В основном они базировались на изощренных трюках, предполагающих особое место Земли во Вселенной (как в модели Птолемея) и противоречащих космологическому принципу. Мы находим их искусственными и ad hoc. Мы считаем ускоренное расширение установленным фактом, который теоретикам следует интерпретировать с минимальным числом дополнительных предположений.
Слегка сокращенный (без потери смысла + некоторые дополнения)перевод статьи Damien A. Easson, Paul H. Frampton, George F. Smoot, Entropic Accelerating Universe
Интерпретация темной энергии
Согласно ОТО и космологическому принципу масштабный фактор $a(t)$ в FRW-метрике удовлетворяет уравнению Фридмана
\begin{equation} H(t)^2 = \left(\frac{\dot{a}}{a} \right)^2 = \left( \frac{8 \pi G}{3} \right) \rho \label{FLequation} \end{equation}
Нормировка $a(t_0) = 1,$ а $\rho$- плотность энергии компоненты, управляющей расширением Вселенной. Установлено, что $\rho$ включает материю и излучение, так что
\begin{equation} \rho \supseteq \rho_{m} + \rho_{\gamma} \label{rho} \end{equation} где $\rho_{m}(t) = \rho_{m}(t_0) a(t)^{-3}$ и $\rho_{\gamma} (t) = \rho_{\gamma}(t_0) a(t)^{-4}$.
Для объяснения наблюдаемого ускоренного расширения наиболее популярный подход – добавить в (1) член с темной энергией ${\rho _{DE}}(t)$ с
\begin{equation} \rho_{DE} (t) = \rho_{DE}(t_0) a(t)^{-3 (1 + \omega)} \label{rhoDE} \end{equation}
с $w = p/\rho {c^2}$. Для случая $w =- 1$ темная энергия является космологической константой. Пренебрегая материей и излучением, уравнение легко проинтегрировать и найти \begin{equation} a(t) = a(t_0) ~ e^{Ht} \label{CC} \end{equation} где $H = \sqrt {\Lambda /3} \; = \sqrt {8\pi G{\rho _{DE}}} $. Дифференцируя (4) $p$ раз по времени, получим \begin{equation} \frac{d^p}{dt^p} a(t) |_{t=0} = (H)^p \label{jerk} \end{equation}
Подстановка в первое уравнение Фридмана плотности тёмной энергии приводит к плодотворной СКМ модели,
\begin{equation} a(t) = a(t_0) ~ e^{Ht} \label{CC1} \end{equation}
где $\sqrt{3} H= \sqrt{\Lambda} = \sqrt {8 \pi G \rho_{DE}}$.
но не позволяет проникнуть в существо темной энергии. Отождествление космологической постоянной с энергией вакуума приводит к проблеме космологической постоянной, которая заключается в том, что наблюдаемое значение плотности тёмной энергии $\rho_{\Lambda_{\rm obs}} \sim (10^{-3} \, \rm eV)^4$ и её теоретически предсказанное значение (в предположении, что в качестве масштаба UVобрезания выбрана планковская длина) $\rho_{\Lambda_{\rm th} }\sim (10^{18} \, \rm GeV)^4$, отличаются на 120 порядков.
В таких условиях мы перейдем к принципиально другому приближению, которое позволяет избежать темной энергии, как в форме космологической константы, так и в форме скалярных полей.
Интерпретация энтропийной силы
Мы теперь будем придерживаться альтернативного подхода, в котором вместо темной энергии центральную роль будут играть идеи информации, голографии, энтропии и температуры.
Первое и единственное предположение есть голография, под которой мы понимаем информацию о Вселенной, закодированную на экране, который трактуется как двумерная поверхность Вселенной.
Согласно С Хокингу на любом горизонте событий имеет место ненулевая темперетура ${T_\beta },$ (на самом деле температура Унру) которую мы можем оценить как
\begin{equation}T_{\beta} = \frac{\hbar}{ k_B }~\frac{H }{ 2 \pi} \sim 3 \times 10^{-30} K\label{T-beta}\end{equation}
Эта температура тесно связана с температурой де Ситтера. Более важно, что температура горизонта (экрана) приводит к сопутствующей энтропийной силе и соответствующему ускорению ${a_{horizon}},$ которой задается соотношением Унру
\begin{equation}a_{Horizon} = \left( \frac{2 \pi c k_B T_{\beta}}{\hbar} \right) = cH\sim10^{-9} \, m/s^2\label{acceleration}\end{equation} (7)
Если мы используем выражение для ${T_\beta }$ мы получим космическое ускорение согласующееся с наблюдаемым.
При таком подходе темная энергия - несуществующий объект. Ее заменяет энтропийная сила действующая на горизонт, далее будет показано, что учет этого эффекта эквивалентен введению темной энергии, обладающей отрицательным давлением т.е. способной объяснить ускоренное расширение Вселенной.
Мы еще раз подчеркнем, что, так как мы ничего не знаем о физике, управляющей квантовыми флуктуациями, приведенные выше аргументы сами по себе не решают проблемы космологической константы. Однако, интерпретация космического ускорения с помощью энтропийной силы помогает понять, почему ускорение наблюдается сегодня таким маленьким, в противоположность гигантскому значению, предсказываемому квантовой теорией поля в комбинации с ОТО.
Ниже мы детально рассмотрим энтропийную трактовку и покажем, что с ее помощью можно понять текущее ускоренное расширение. Далее последует вывод выражения для давления, которое отрицательно и поэтому представляет давление в направлении экрана. Нижеследующие результаты базируются на фундаментальных принципах термодинамики и не зависят ни от каких моделей.
Энтропия на хаббловском горизонте, т.е на поверхности радиуса ${R_H} = c/H$, есть
\begin{equation}S_H = \frac{k_B c^3}{G \hbar} \frac{A}{4} = \frac{k_B c^3} {G \hbar} \pi R_H^2 = \frac{k_B c^3} {G \hbar} \pi \left( \frac{c}{H} \right)^2 \sim (2.6 \pm 0.3) \times 10^{122} k_B\end{equation} (8)
Увеличение хаббловского радиуса ${R_H}$ на величину $\Delta r$ приводит к увеличению энтропии на величину $\Delta {S_H}$
$$\Delta {S_H} = {k_B}\frac{{{c^3}}}{{G\hbar }}2\pi {R_H}\Delta r = {k_B}\frac{{{c^3}}}{{G\hbar }}2\pi \left( {\frac{c}{H}} \right)\Delta r \approx 2(2.6 \pm 0.3) \times {10^{122}}{k_B}$$ (9)
Энтропийная сила
\begin{equation}F_r = - \frac{dE}{dr} = - T\frac{dS}{dr} = - T_\beta \frac{ d S_H}{d r} = - \frac{\hbar}{ k_B }~\frac{ H }{ 2 \pi} \frac{k_B c^3} {G \hbar} 2\pi \left( \frac{c}{H} \right) = - \frac{c^4 }{ G}\end{equation} (10)
Давление, оказываемое этой силой на космологический горизонт
\begin{equation}P = \frac{F_r}{A} = - \frac{1}{A} T \frac{dS}{dr} = - \frac{1}{A} \frac{c^4 }{ G} = - \frac{1}{ 4 \pi c^2/H^2} \frac{c^4 }{ G} = - \frac{c^2 H^2 }{4 \pi G} = - \frac{2}{3} \rho_{critical} c^2\end{equation} (11)
Это значение близко к измеренному давлению (натяжению) темной энергии в форме космологической константы. В голографическом подходе натяжение возникает не за счет отрицательного давления темной энергии, а за счет энтропийного натяжения, обязанного энтропийному содержанию на голографическом экране. Наличие такого натяжения эквивалентно направленному вовне ускорению ${a_H} = cH$.
Ускорение в следствии энтропии и поверхностных слагаемых
В этом разделе мы представим своеобразную феноменологическую модель, инспирированную поверхностными членами, которые обычно игнорируются в ОТО. Мы покажем, что такая модель приводит к ускоренно расширяющейся Вселенной. Хотя поверхностные члены являются источниками нашего «вдохновения», модель следует рассматривать как феноменологическую без претензий на строгость. Мы сделаем небольшое дополнительное предположение, состоящее в корректности ОТО. Мы покажем, что при разумных предположениях новые члены генерируют ускоренную динамику, описываемую FLRWуравнениями. Имеются решения, соответствующие переходу от фазы замедленного расширения к ускоренному. Подчеркнем, что наш основной результат – космологическое ускорение обязано энтропийной силе – является модельно независимым.
Схематически действие Эйнштейна-Гильберта, включающее поверхностный член, и действие для материи, можно представить в виде
$$I = \int_M {(R + {L_m})} + \frac{1}{{8\pi }}\int_{\partial M} K$$(12)
где$R$- скалярная кривизна,${L_m}$- лагранжиан для материи и$K$- это слагаемое, пропорциональное кривизне граници. Вариационная процедура приводит к обычным уравнениям Эйнштейна с дополнительным поверхностным членом (поверхностная энергия)
$${R_{\mu \nu }} - \frac{1}{2}R{g_{\mu \nu }} = \frac{{8\pi G}}{{{c^4}}}{T_{\mu \nu }} + surface\;terms$$(13)
Обычно поверхностными членами пренебрегают, несмотря на то, что он может играть существенную роль в полевых уравнениях в случае присутствия у системы горизонта. В случае сферической симметрии и однородности приходим к уравнениям Фридмана-Леметра:
Ускорение масштабного фактора = замедлению от материального содержания Вселенной + ускорение от поверхностных членов
$$\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}}} \right) + {a_{surface}}/{d_H}$$(14)
Имеется ряд приближений для определения формы новых членов. Здесь мы используем простейшую возможность. Из нашей мотивировки поверхностного члена можно ожидать, что интеграл от шпура внутренней кривизны будет того же порядка что и слагаемое с поздневременным (late time) ускорением.
$$6\left( {2{H^2} + \dot H} \right)$$
Так что поверхностный член приближенно равен
$$\frac{{6\left( {2{H^2} + \dot H} \right)}}{{8\pi }} = \frac{3}{2}{H^2} + \frac{3}{4}\dot H = \frac{3}{2}\left( {{H^2} + \frac{1}{2}\dot H} \right)$$
Мы можем также использовать энтропийные идеи и увидеть, что они естественно приводят к медленно расширяющейся Вселенной
Хорошо известно, что имеются кривизна и температура, ассоциирующиеся с горизонтом, причем эти величины связаны друг с другом. Температура $T$ представляет температуру Унру, де Ситтера или Хокинга. Мы можем тогда связать поверхностную энтропию или поверхностный член с его температурой и его ускорением. Используя (7), найдем для ускорения горизонта
$${a_{surface}} = {a_{entropic}} = cH$$Естественным масштабом для нашей задачи является хаббловский радиус ${{d}_{H}}=c/H$ и, следовательно,
$\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}}} \right) + {H^2}$ (16)
Замечательно, что этот результат с точностью до фактора $3/2\pi $ совпадает с предварительной оценкой. С температурой Хокинга коэффициент должен равняться $1/2$. Имеется некоторая свобода, которую мы используем для получения хороших результатов в двух предельных случаях. Легко показать, что, если член ${H^2}$ доминирует над $\frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}}} \right),$ то решение уравнения соответствует пространству де Ситтера с масштабным фактором
$a(t) = a\left( {{t_0}} \right){e^{H(t - {t_0})}}$
Альтернативное уравнение
$$\frac{{\ddot a}}{a} = - \frac{{4\pi G}}{3}\left( {\rho + \frac{{3P}}{{{c^2}}}} \right) + \frac{3}{{2\pi }}{H^2} + \frac{3}{{4\pi }}\dot H$$ (17)
Может обеспечить лучшее согласование с экспериментальными данными и более строгий вывод, но не имеет простоты уравнения (16).
Сравнение с данными по сверхновым звёздам
Мы закончим демонстрацией возможности энтропийного механизма, вызванного поверхностными членами обеспечить прекрасное согласование данных по суперновым в предположении, что работает простое уравнение (17). Так как мы используем метрическую теорию гравитации, мы можем использовать и стандартную формулу для фотометрического расстояния
${d_L}(z;H(z),{H_0}) = \frac{{c(1 + z)}}{{{H_0}}}\int_o^z {\frac{{dz'}}{{H(z')}}}$ (19)
Оказывается, что энтропийные силы могут обеспечить прекрасное согласование наблюдательных данных (см. Рис.1). Энтропийные модели обеспечивают гладкий переход от фазы замедленного к фазе ускоренного расширения при $z\sim 0.5,$ как и в $\Lambda CDM$
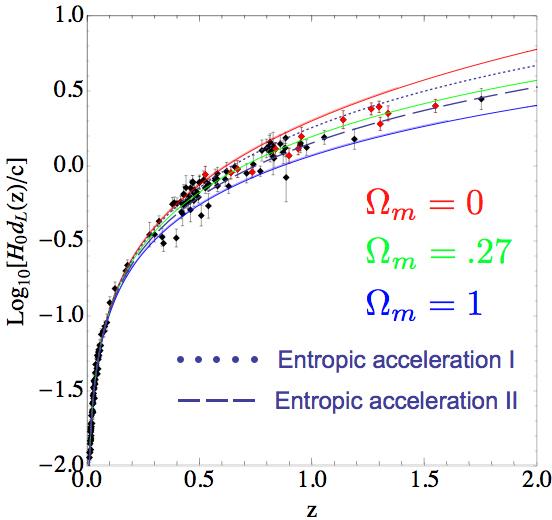
Рис. 1. Сравнение космологических моделей с энтропийным ускорением и некоторых $\Lambda CDM$ моделей. На рисунке приведено фотометрическое расстояние $d_L$ для модели (16 ) I и (17) II.
Заключение.
Мы предложили теорию ускоренного расширения Вселенной, базирующуюся на энтропийных силах. В этой теории физическое понимание ускоренного расширения достигается без темной энергии. В этом подходе ускоренное расширение есть неотвратимое следствие хранения голографической информации на экране, совпадающим с горизонтом Вселенной.
Нет комментариев.
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.