Информация в голографической Вселенной
На вопрос «из чего состоит физический мир» вам скорее всего ответят – «из вещества и энергии». Однако образованный человек непременно упомянет и об информации, которая играет ключевую роль в живой и даже неживой природе. Согласно же теории Джона Уилера (John A. Wheeler) из Принстонского университета, физический мир состоит именно из информации, а вещество и энергия играют в нем второстепенную роль.
Такая точка зрения заставляет по новому взглянуть на старые проблемы. Информационная емкость различных устройств, таких как дисковые накопители, растет очень быстро. Когда этот процесс остановится? Каков предел информационной емкости прибора массой, скажем, в один грамм и объемом не более кубического сантиметра (размер микросхемы)? Какое количество информации необходимо для полного описания Вселенной? Может ли оно уместиться в памяти компьютера? Можем ли мы, как писал когда-то Уильям Блейк (Whilliam Blake), «увидеть мир в песчинке» или это лишь поэтический образ?
Новейшие успехи теоретической физики дают ответы на некоторые из этих вопросов и помогают создавать теорию реальности. Изучая таинственные свойства черных дыр, физики вывели абсолютный предел объема информации, которую может хранить данная область пространства или данные количества вещества и энергии. Результаты исследований заставляют задуматься о том, что наша Вселенная, воспринимаемая нами как трехмерная, в действительности может быть «написана» на двухмерной поверхности подобно голограмме. При этом наше восприятие мира как трехмерного может быть либо заблуждением, либо одним из альтернативных способов видения реальности. Песчинка не может заключать в себе весь наш мир, а плоский экран – может.
История двух энтропий
В основе формальной теории информации лежит разработка американского математика Клода Шеннона (Claud E. Shannon), опубликованная в 1948 г. Он ввел наиболее употребительную меру информационного содержания – энтропию, которая долгое время была центральным понятием термодинамики и которую обычно определяют как меру неупорядоченности физической системы. В 1877 г. австрийский физик Людвиг Больцман определил энтропию как число различных микроскопических состояний, которые может принимать совокупность частиц, составляющая некий «кусок» вещества, оставаясь на вид той же макроскопической «частью».
Например, для воздуха в комнате можно рассчитать все возможные пространственные распределения молекул и все их возможные движения. Для описания способа количественного выражения информации, содержащейся, например, в сообщении, Шеннон предложил формулу, совпадающую с формулой Больцмана. По Шеннону, энтропия сообщения – это число двоичных знаков, или битов, необходимое для кодирования данной информации. Энтропия не отражает ценность сообщения, которая полностью зависит от контекста, однако в качестве объективной меры количества информации она оказалась чрезвычайно полезной.
В частности, знание энтропии необходимо для проектирования любого современного коммуникационного устройства – от сотового телефона до модема и проигрывателя компакт-дисков. В концептуальном отношении термодинамическая энтропия и энтропия Шеннона эквивалентны: число распределений, подсчитываемое энтропией Больцмана, отражает количество шенноновской информации, необходимое для реализации любого конкретного распределения. Однако есть существенные различия. Во-первых, энтропия, которой пользуются химики, выражается отношением энергии к температуре, а энтропия Шеннона, используемая специалистами по связи, – числом битов, т.е. величиной принципиально безразмерной. Однако даже приведенные к одним и тем же единицам измерения численные значения этих величин будут различны. Так, информационная энтропия микросхемы, хранящей один гигабайт данных, составляет около $10^{10}$ бит (1 байт = 8 бит), а термодинамическая энтропия той же микросхемы при комнатной температуре имеет порядок $10^{23}$ бит.
ОБЗОР: МИР КАК ГОЛОГРАММА
Различие объясняется тем, что они рассчитываются для различного числа степеней свободы (это любая величина, которая может изменяться; например, координата, определяющая положение частицы в пространстве.) Энтропия Шеннона характеризует только состояние каждого из микроскопических транзисторов, сформированных в кристалле кремния. Транзистор может находиться в одном из двух состояний – открытом или закрытом, которым соответствуют двоичные ноль и единица. Значит, он имеет одну двоичную степень свободы, в отличие от термодинамической энтропии, зависящей от состояний миллиардов атомов (и их странствующих электронов), образующих транзистор. По мере того, как миниатюризация неуклонно приближает день, когда каждый атом сможет хранить один бит информации, численное значение полезной информационной энтропии микросхемы будет приближаться к значению термодинамической энтропии материала, из которого она изготовлена. Когда обе вычисляются для одинакового числа степеней свободы, они равны. Каково предельное число степеней свободы? Атомы состоят из электронов и ядер, являющихся скоплением протонов и нейтронов, которые, в свою очередь, состоят из кварков.
Многие физики считают электроны и кварки возбужденными состояниями суперструн, являющихся наиболее фундаментальными природными объектами. Однако в структуре нашей Вселенной может оказаться больше уровней, чем полагает современная физика. Чтобы рассчитать предельную информационную емкость некоего количества вещества или, что эквивалентно, его истинную термодинамическую энтропию, необходимо знать природу фундаментальных составляющих вещества или самого глубокого уровня его структуры, который я назову уровнем Х.
Термодинамика черных дыр
Согласно уравнениям общей теории относительности, разработанной Альбертом Эйнштейном в 1915 г., достаточно большая концентрация вещества или энергии может искривить пространство-время настолько, что оно разорвется, образовав черную дыру. Законы относительности не позволяют чему бы то ни было, попавшему внутрь нее, появиться вновь, по крайней мере, в рамках представлений классической (неквантовой) физики. Важнейшее значение имеет рубеж невозврата, называемый горизонтом событий черной дыры. В простейшем варианте он представляет собой сферу, радиус которой тем больше, чем больше масса черной дыры. Узнать, что находится внутри нее, невозможно, т.к. никакая информация не может преодолеть этот горизонт. Однако, исчезая навсегда, вещество оставляет некоторые следы: его энергия (в соответствии с уравнением Эйнштейна $E = mc^2$ мы считаем массу энергией) навсегда увеличивает ее массу.
Если перед захватом вещество обращалось вокруг черной дыры, его момент импульса добавляется к моменту импульса дыры. И массу, и момент импульса черной дыры можно определить по их влиянию на пространство-время в ее окрестности. Таким образом, законы сохранения энергии и импульса применимы к черной дыре. Но второй закон термодинамики, кажется, нарушается. Этот закон запрещает обратимые процессы, а значит, энтропия изолированной физической системы не может уменьшаться – в лучшем случае она остается постоянной, но обычно растет. Этот закон – основа физической химии и техники. Как впервые отметил Уилер, когда вещество исчезает в черной дыре, его энтропия тоже пропадает навсегда, что представляется нарушением второго закона термодинамики. Ключ к этой разгадке появился в 1970 г., когда аспирант Уилера в Принстонском университете Деметриус Христодулу (Demetrious Christodoulou) и Стивен Хокинг (Stephen W. Hawking) из Кембриджского университета независимо друг от друга доказали, что при слиянии черных дыр общая площадь горизонта событий никогда не уменьшается.

Это навело меня в 1972 г. на мысль, что энтропия черной дыры пропорциональна площади поверхности ее горизонта событий. Я предположил, что при падении вещества в черную дыру возрастание ее энтропии компенсирует или превосходит «потерю» энтропии вещества. Сумма энтропии черной дыры и обычной энтропии вне ее не может уменьшаться. Таков обобщенный второй закон (ОВЗ) термодинамики. Когда звезда коллапсирует, превращаясь в черную дыру, энтропия дыры оказывается гораздо больше энтропии звезды. В 1974 г. Хокинг показал, что черная дыра спонтанно испускает тепловое излучение, известное сегодня как излучение Хокинга.
Это явление не согласуется с теоремой Христодулу–Хокинга (масса черной дыры и, следовательно, площадь ее горизонта уменьшается), но ОВЗ разрешает противоречие: энтропия испускаемого излучения компенсирует уменьшение энтропии черной дыры, так что ОВЗ соблюдается. В 1986 г. Рафаил Соркин (Rafael D. Sorkin) из Сиракьюзского университета сравнил роль горизонта событий черной дыры с барьером, не допускающим влияния информации, находящейся внутри дыры, на события вне ее, чтобы показать, что ОВЗ должен соблюдаться во всех процессах, касающихся черной дыры. Его глубокие рассуждения ясно показывают, что энтропия ОВЗ учитывает все уровни до Х включительно, как бы глубоко тот ни лежал.
Процесс излучения Хокинга позволил ему определить коэффициент пропорциональности между энтропией черной дыры и площадью горизонта событий: энтропия равна одной четверти площади горизонта, выраженной в планковских единицах (планковская единица площади – это квадрат длины Планка, фундаментальной константы, связанной с тяготением и квантовой механикой, близкой к $10^{–33}$ см). Это огромная величина даже по термодинамическим представлениям. Энтропия черной дыры диаметром 1 см составляет около $10^{66}$ бит, что примерно равно термодинамической энтропии водяного куба с ребром в 10 млрд. км.
Мир как голограмма
Обобщенный второй закон термодинамики позволяет найти предел информационной емкости любой изолированной физической системы, т.е. предельный объем информации, которая может храниться на всех уровнях ее структуры до уровня Х включительно. В 1980г. я начал изучать универсальный энтропийный предел, определяющий максимальный объем информации для данной массы данного размера. Связанный с ним голографический предел, устанавливающий максимальное значение энтропии, которая может содержаться в веществе и энергии, занимающих данный объем пространства, был рассмотрен в 1995 г. Леонардом Зускиндом (Leonard Susskind) из Стэнфордского университета. Если изолированная масса приблизительно сферической формы, не являющаяся черной дырой и ограниченная замкнутой поверхностью с площадью A, коллапсирует, превращаясь в черную дыру, то площадь ее горизонта событий станет меньше A. Следовательно, энтропия черной дыры будет меньше $A/4.$ Согласно ОВЗ, энтропия не может уменьшаться, значит, первоначальная энтропия рассматриваемой массы не могла быть больше $A/4.$ Из этого следует, что энтропия изолированной физической системы, ограниченной поверхностью площади $A,$ всегда меньше $A/4.$ А что если масса спонтанно не коллапсирует?
В 2000 г. я показал, что маленькая черная дыра может быть использована для превращения системы в черную дыру, мало чем отличающуюся от рассмотренной Зускиндом. Таким образом, предел за- висит только от ОВЗ, а не от строения системы или природы уровня Х. Теперь мы можем ответить на некоторые вопросы о пределах возможности хранения информации. Устройство поперечником в 1 см может хранить до $10^{66}$ бит, в то время как вся видимая Вселенная содержит не менее $10^{100}$ бит энтропии. Это количество может, в принципе, быть размещено в пределах сферы диаметром 0,1 светового года. Но оценка энтропии Вселенной – трудная задача, для решения которой понадобятся гораздо большие числа, требующие сферы размером с саму Вселенную.
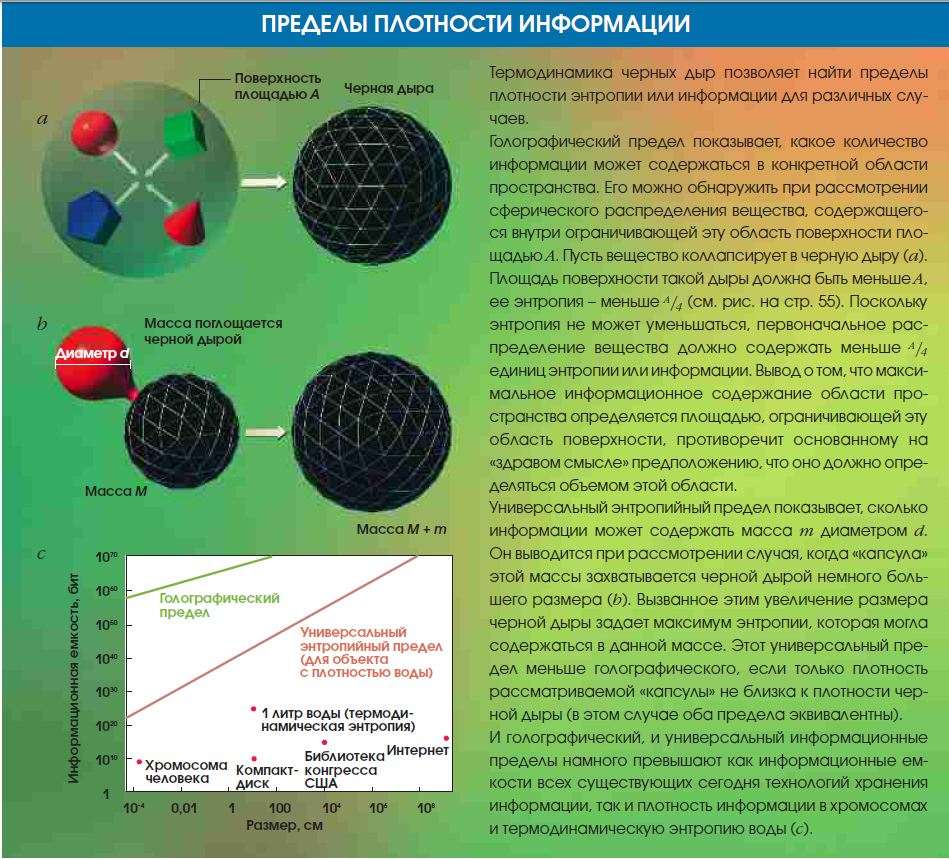
У голографического предела есть и другой аспект: максимум возможной энтропии определяется площадью границы, а не заключенным в ней объемом. Представим, что мы составляем большую систему из микросхем памяти. Число транзисторов, определяющее информационную емкость, будет расти пропорционально ее объему. Так же будет возрастать и общая термодинамическая энтропия совокупности микросхем. Примечательно, что теоретически предельная информационная емкость области пространства, занимаемой такой системой, будет увеличиваться только пропорционально площади поверхности этой области. Поскольку объем растет быстрее площади поверхности, рано или поздно суммарная энтропия всех микросхем превысит голографический предел. Создается впечатление, что должны потерпеть крах либо наши представления об энтропии и информационной емкости, либо ОВЗ. На самом деле построить такую систему невозможно: под действием внутренних гравитационных сил она сколлапсирует, превратится в черную дыру, раньше, чем будет достигнут упомянутый предел.

После этого каждая добавленная микросхема будет увеличивать массу и площадь поверхности черной дыры таким образом, что ОВЗ будет сохраняться. Если верен голографический принцип, предложенный в 1993 г. нобелевским лауреатом Герардом Хофтом (Gerard’t Hooft) из Утрехтского университета в Нидерландах и развитый Зускиндом, то зависимость предела информационной емкости от площади поверхности, а не от объема вполне объяснима. В повседневной жизни голография – это особый вид фотографии, позволяющий получать трехмерные изображения при использовании специального освещения. Вся информация кодируется в виде системы темных и светлых областей на двумерной поверхности фотопленки и всегда готова к воспроизведению.
Голографический принцип гласит, что подобным образом можно полностью описать любую физическую систему, занимающую некую область трехмерного пространства: он утверждает, что другая физическая теория, определенная только для двухмерной границы этой области, способна полностью описать физику ее трехмерного содержимого. Если объемная система может быть полностью описана теорией, действующей только на двумерной границе этой системы, то можно ожидать, что информационное содержание системы не будет превышать аналогичного показателя ее двумерной «оболочки».
Вселенная, нарисованная на ее границе
Можно ли применить голографический принцип ко всей Вселенной? Реальная Вселенная – это четырехмерная система, у которой есть объем, и она простирается во времени. Если ее физика голографична, должен существовать другой набор физических законов, действующих где-то на трехмерной границе четырехмерного пространства-времени. Какую поверхность следует использовать в качестве границы Вселенной?
Один из путей к осмыслению этих новых идей лежит в изучении моделей, более простых, чем реальная Вселенная. Примерами действия голографического принципа стали так называемые антидеситтеровские пространства-времена. Исходное пространство-время де Ситтера – это модель Вселенной, впервые построенная в 1917 г. нидерландским астрономом Виллемом де Ситтером (Willem de Sitter) как решение уравнений Эйнштейна, включающее силу отталкивания, называемую космологической постоянной. Пространство-время де Ситтера пусто, расширяется с ускорением и обладает высокой симметрией. В 1997 г. астрономы, наблюдавшие взрывы далеких сверхновых, пришли к выводу, что расширение нашей Вселенной ускоряется, и она, вероятно, будет приближаться к деситтеровскому пространству-времени. Если в уравнениях Эйнштейна отталкивание заменить притяжением, решение де Ситтера окажется антидеситтеровским пространством-временем, обладающим столь же высокой симметрией. Кроме того, это пространство-время имеет границу, находящуюся на бесконечном удалении, и во многом оно подобно нашему привычному пространству-времени.
ОБ АВТОРЕ:
Якоб Бекенштейн (Jacob D. Bekenstein) – профессор теоретической физики Еврейского университета в Иерусалиме, член Израильской Академии естественных и гуманитарных наук и лауреат премии Ротшильда. Он является одним из основателей термодинамики черных дыр и внес весомый вклад в изучение различных аспектов связи между информацией и тяготением. Бекенштейн посвящает эту статью Джону Уилеру (John Archibald Wheeler), который был руководителем его диссертации 30 лет назад.
Используя антидеситтеровское пространство-время, теоретики показали пример действия голографического принципа: Вселенная, описываемая теорией суперструн, действующей в антидеситтеровском пространствевремени, полностью эквивалентна квантовой теории поля, действующей на границе этого пространства-времени. Первым предположение о таком соотношении для пятимерного антидеситтеровского случая высказал в 1997 г. Хуан Малдасена (Juan Maldacena) из Гарвардского университета. Впоследствии для ряда случаев оно было подтверждено Эдвардом Виттеном (Edward Witten) из Принстонского института передовых исследований (шт. Нью-Джерси), а также Стивеном Габсером (Steven S. Gubser), Игорем Клебановым и Александром Поляковым из Принстонского университета.

Сегодня примеры этого голографического соответствия известны для пространств с различным числом измерений. Таким образом, две теории, казавшиеся совершенно разными и даже действующими в пространствах с разным числом измерений, оказались эквивалентны. Голографическая эквивалентность, возможно, позволит нам заменить сложные вычисления таких явлений, как поведение кварков или глюонов в четырехмерном граничном пространстве-времени, более простыми вычислениями в высокосимметричном пятимерном антидеситтеровском пространстве-времени. Это соответствие работает и в другом отношении. Уиттен показал, что черная дыра в антидеситтеровском пространстве-времени соответствует горячему излучению в альтернативной физике, действующей в граничном пространстве-времени. Загадочная энтропия черной дыры свелась к вполне понятной энтропии излучения.
Расширяющаяся Вселенная
Высокосимметричная и пустая пятимерная антидеситтеровская Вселенная мало похожа на нашу Вселенную, существующую в четырехмерном пространстве-времени и заполненную веществом и энергией. Даже представив нашу реальную Вселенную моделью, в которой вещество и излучение распределены равномерно, мы получим не антидеситтеровскую вселенную, а вселенную Фридмана–Робертсона–Уокера (ФРУ). Сегодня многие космологи согласны, что наша Вселенная подобна вселенной ФРУ, которая бесконечна, не имеет границ и будет вечно расширяться. Согласуется ли такая Вселенная с голографическим принципом или с голографическим пределом? Рассуждения Зускинда, основанные на рассмотрении коллапса с образованием черной дыры, не могут ответить на этот вопрос. Действительно, в однородной расширяющейся Вселенной голографический предел, выведенный из анализа черных дыр, должен нарушаться.
Энтропия области, однородно заполненной веществом и излучением, действительно пропорциональна объему этой области, следовательно, при достаточно большом ее размере голографический предел неизбежно будет превышен. В 1999 г. Рафаил Буссо (Raphael Bousso), работавший тогда в Стэнфордском университете, предложил модифицированный голографический предел, который, как оказалось, применим даже в тех случаях, когда рассмотренные выше пределы неприменимы. Буссо начинает с рассмотрения любой двумерной поверхности, которая может быть замкнутой, как сфера, или открытой, подобно листу бумаги. Представьте себе короткую вспышку света, испускаемую одной стороной этой поверхности так, что лучи выходят перпендикулярно к ней в каждой точке. Единственное требование – изначальная сходимость лучей. Такому требованию отвечает, например, внутренняя поверхность сферической оболочки.
Буссо рассматривает энтропию вещества и излучения, через которые проходят эти воображаемые лучи, в пределах до тех точек, где они начинают пересекаться. Он предполагает, что эта энтропия не может быть больше энтропии рассматриваемой поверхности, т.е. больше четверти ее площади в планковских единицах. Такой подход к расчету энтропии отличен от применявшегося для расчета первоначального голографического предела. Предел Буссо характеризует не энтропию области в некоторый момент времени, а сумму энтропий отдельных подобластей в различные моменты времени – те, когда они «освещаются» вспышкой от поверхности. Предел Буссо включает в себя другие пределы энтропии, но при этом он свободен от их недостатков. Из него можно вывести и универсальный энтропийный предел, и голографический предел Хофта–Зускинда для любой не слишком быстро изменяющейся изолированной системы с не слишком сильным гравитационным полем. Когда вышеуказанные условия не действуют, например, при коллапсе шара из вещества, уже находящегося внутри черной дыры, эти пределы становятся неприменимыми, а предел Буссо работает. Ученый также показал, что такой подход можно использовать для выявления двумерных поверхностей, на которых может быть «записана» голограмма мира.
Пророки революции
Ученые предложили существование многих других пределов для энтропии. Но хотя голографический подход осмыслен еще не до конца, от него, видимо, уже невозможно отказаться, а господствовавшее 50 лет представление, будто теория поля является последним словом физики, придется пересмотреть. Такие поля, как электромагнитное, изменяются от точки к точке непрерывным образом и, следовательно, допускают неограниченное число степеней свободы.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА НА АНГЛИЙСКОМ ЯЗЫКЕ:
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА НА РУССКОМ ЯЗЫКЕ:
Допускает его и теория суперструн. Голография же ограничивает число степеней свободы, которые могут существовать внутри граничной поверхности, конечным значением. Теория поля с ее бесконечностью не может быть последним словом. Более того, даже если бесконечность удастся «приручить», придется как-то оправдывать таинственную зависимость информации от площади поверхности. Толчком к созданию более совершенной теории может оказаться голография. Какой должна быть фундаментальная теория? Цепь рассуждений, включающих в себя голографические представления, привела некоторых ученых, в частности Ли Смолина (Lee Smolin) из Института теоретической физики в Ватерлоо, к предположению, что такая фундаментальная теория должна иметь дело не с полями и даже не с пространством-временем, а с обменом информацией между физическими процессами. Если это так, то видение информации как «материала», из которого построен мир, найдет достойное воплощение.
Комментарии (2):
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.






Один из сюрпризов недавних лет является успешное применение теорфизики "высокого полета" (AdS/CFT сответствия) к описанию таких обыденных процессов, как столковение высокоэнергетических тяжелых ядер (такие процессы изучаются в эксперименте RHIC). Сюрпризом это является прежде всего для тех, которые думают, что для описания экспериментальных данных хватит "обычной", общепонятной математики, а всё мудреное -- это от лукавого.
Суть заключается в том, что некоторая разновидность калибровочной теории -- N=4 суперсиметричная теория Янга-Миллса (N=4 SYM) в пределе большого числа цветов -- находит применение при описании адронной материи при высоких температурах. Очень непохожая на обычную КХД при нулевой температуре, эта теория начинает ее напоминать при повышении температуры. Однако она существенно проще, чем сама КХД, и самое главное, к ней применимо AdS/CFT соответствие, позволяющее свести динамику кварков и глюонов в режиме сильной связи к изучению гравитации в неком многомерном пространстве.