Хотя теория струн была описана выше как теория квантовой гравитации, она возникла как попытка описать адроны. Струнное описание объяснило некоторые особенности спектра адронов, типа траекторий Редже, и т.д . Мы теперь знаем, что адроны описываются QCD, но нам все еще весьма трудно делать вычисления при низких энергиях из-за большой константы взаимодействия. Фактически мы ожидаем конфайнмента.

Заключительная часть перевода, уже ставшей классикой статьи Juan Maldacena. Gravity, particle physics and their unification

Первая часть статьи и вторая

Популярную версию статьи этого же автора: Черные дыры и структура пространства-времени

Подборка статей по теории струн

Настоятельно рекомендуется также ознакомится со статьей Голографический принцип: не первая встреча - некоторые её части будут нужны в дальнейшем

Конфайнмент, как думают, является результатом того факта, что линии цветного электрического поля образуют узкие связки при движении от кварка до антикварка, см. Рисунок 5.

Эти потоки выглядят при низких энергиях подобно струнам, и можно ожидать, что при низких энергиях применимо описание в терминах струны, 't Hooft показал [8], что надлежащий способ понимать эти струны состоит в том, чтобы перейти к пределу большого количества цветов $N\to \infty$, сохраняя $g^2_{YM}N$ постоянным. В этом пределе выживают только планарные фейнмановские диаграммы. Эти планарные фейнмановские диаграммы, кажется, дают дискретизацию мировой поверхности струны.

Рис. 5: Потоки цветового электрического поля формируют узкую связку, приводящую к линейному потенциалу и конфайнменту.

Однако не было ясно, какая именно теория струн здесь должна получиться. Для случая теории Янга-Миллса с $N=4$ суперсимметрией и большого количества цветов N было предположено, что эти калибровочные струны являются теми же самыми фундаментальными струнами, описанными выше, но перемещающимися в специальном искривленном пространстве-времени: в произведении пятимерного анти-де-ситтерова пространства и 5-сферы [4]. Пятимерное AdS имеет границу, которая является четырехмерной. Теория поля определена на этой четырехмерной границе. На рисунке 6 мы можем видеть диаграмму Пенроуза для AdS.

Радиус кривизны этого пространства-времени пропорционален $\left(g^2_{YM}N\right)^{1/4}$ и константа взаимодействия струны будет $g_s=g^2_{YM},$ она ведет себя подобно $1/N$ при фиксированном $g^2_{YM}N,$ как и ожидалось из общих соображений 't Hooft. Имеется большое количество проверок этого соответствия. Множество проверок делается возможным из-за большого количества суперсимметрий. Самая простая проверка - наблюдение, что обе теории имеют ту же самую симметрию. $N= 4$ суперсимметричная теория Янга-Миллса масштабно-инвариантна, константа взаимодействия не является бегущей, она не зависит от энергии. Не суперсимметричный Янг-Миллс классически конформно инвариантен, но квантовые поправки вводят масштаб длины через бегущую константу взаимодействия. В конформных теориях группа симметрии включает трансляции, вращения, масштабные преобразования и так называемые специальные конформные преобразования. Все они образуют группу, математически известную как $SO(2, 4).$ Эта группа - группа изометрий AdS. Подобным образом, теория Янга-Миллса имеет глобальную группу симметрии $SO(6)$, которая является той же самой, что и группа вращений $S^5$. Фактически, когда мы рассматриваем теорию струн на $AdS_5 \times S^5$, мы имеем те же самые мы имеем те же самые суперсимметрии, что и в калибровочной теории.

Рис. 6: Диаграмма Пенроуза для анти-де-ситтерова пространства, иллюстрирующая его причинную структуру. Это цилиндр. Время течет в вертикальном направлении. Граница $AdS -$ - граница цилиндра. В случае $AdS_5$ границей является $R \times S^3.$

Другие проверки включают сравнение спектра BPS-частиц, потоки ренормгруппы, которые частично нарушают суперсимметрию и т.д. Многие обобщения этого соответствия были предложены для других теорий с меньшей суперсимметрией или вовсе без суперсимметрии и для теорий, которые не являются конформно инвариантными. Детальный список этих проверок и более обширный список ссылок по этой теме см. в [7]. Загадочным аспектом является то, что теория внутри объема содержит гравитацию, в то время как полевая теория гравитации не содержит. Гравитация в объеме связана с тензором напряжений граничной теории следующим образом. Корреляционные функции для тензора напряжений в полевой теории приравниваются амплитуде распространения гравитонов между заданными точками на границе. Корреляционные функции операторов в полевой теории могут быть рассчитаны, используя это соответствие, как амплитуды распространения частиц в объеме между заданными точками границы [5, 11], см. Рисунок 7. Каждый оператор соответствует частице, или более точно, моде струны, распространяющейся в AdS. Масса частицы в AdS связана с конформной размерностью $\Delta$ поля формулой $$\Delta =2+\sqrt{4+(mR_{AdS})^2}$$

Рис. 7: Корреляционная функция операторов в граничной теории может быть рассчитана как амплитуда вероятности того, что частицы, связанные с операторами, перемещаются между теми точками на границе, где вставлены эти операторы.

Подобно этому мы можем вычислить кварк-антикварковый потенциал, рассматривая струну, которая распространяется между двумя точками границы, см. Рисунок 8. На этом изображении мы видим, что струны, которые двигаются в десятимерном пространстве - это в точности струны, представляющие потоки цветовых полей. Мы можем таким образом говорить, что струны, сделанные из глюонов выглядят очень похожими на обычные фундаментальные струны, когда $g^2_{YM}$ велико. Это общая особенность дуальностей - то, что некоторые возбуждения, которые выглядят фундаментальными в одной картине являются коллективными возбуждениями в дуальной теории. Когда мы вычисляем кварк-антикварковый потенциал, рассчитывая энергию струны на этом искривленном фоне, мы находим, что она ведет себя подобно $V(L)\sim -1/L,$ где $L -$ расстояние в четырехмерной теории. Этот потенциал не дает конфайнмента, его и не должно быть, так как теория поля конформна. Можно деформировать теорию поля таким образом, что при низких энергиях конформная инвариантность и суперсимметрия будут нарушены.

Результирующая теория, как ожидается, будет давать конфайнмент. Действительно можно найти соответствующее решение в супергравитации и получить, что геометрия деформирована, и теперь кварк- антикварковый потенциал действительно будет удерживающим, и теория будет иметь массовую щель [6].

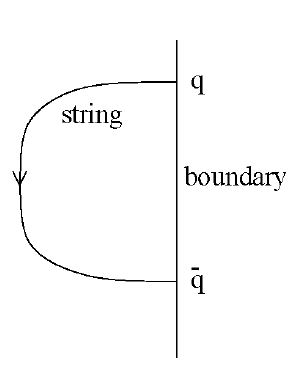
Рис. 8: Кварк-антикварковая конфигурация. Поток цветового поля соединяет кварк с антикварком, это описывается струной, которая перемещается в геометрии высшей размерности, дуальной к теории поля. Потенциал может быть рассчитан как собственная энергия этой струны в искривленной геометрии.

Даже при том, что теория дает конфайнмент, это будет не чистый Янг-Миллс, а его сильновзаимодействующая версия. Чтобы найти предел большого N для чистого Янг-Миллса требуется рассмотреть струны, распространяющиеся в искривленном пространстве-времени, кривизна которого имеет порядок масштаба струны. В этой ситуации гравитационное приближение не является достаточно хорошим. Трактовка струн в этих маленьких пространствах - весьма стимулирующая проблема, которая сейчас изучается. То что мы до сих пор рассматривали было приложениями нашего соответствия к изучению теории поля с большой константой связи при больших N. Соответствие может также быть использовано для того, чтобы больше узнать о гравитации. Использовать его в этом направлении труднее, так как теория поля является сильно взаимодействующей и поэтому трудно поддается решению. Можно сделать, однако, некоторые общие утверждения. Один из наиболее таинственных объектов в теории гравитации - черная дыра. Можно рассмотреть черную дыру в AdS. Эта черная дыра, в принципе, описывается некоторым тепловым состоянием граничной теории. Если у нас имеется большая черная дыра, размера порядка радиуса AdS ее энтропия будет обратно пропорциональна константе Ньютона, которая имеет порядок $1/N^2.$ Так что энтропия будет иметь порядок $N^2,$ что согласуется с числом, получить которое мы наивно ожидали бы в теории поля, исходя из того, что у нас имеется $N^2$ глюонов. В случае $AdS^3$ можно точно вычислить энтропию в теории поля и результат точно согласуется с гравитацией, см. обзор [7].

Аспект гравитации, который проявляется явным образом в этом соответствии - это голография [13, 12]. Голография говорит, что в квантовой теории гравитации мы должны быть способны описать физику в некоторой области пространства теорией с одной степенью свободы (самое большее) на планковскую единицу площади. Обратите внимание, что число степеней свободы тогда росло бы как площадь, а не как объем, к чему мы привыкли. Конечно, для всех физических систем, с которыми мы обычно сталкиваемся, число степеней свободы намного меньше, чем площадь, так как планковская длина слишком мала. Это называется "голографией", потому что аналогично голограмме, которая может хранить трехмерное изображение на двумерной поверхности. В этом случае мы представляем физику пятимерного анти-де-ситтерова пространства-времени с помощью теории, которая живет на ее границе. Это конкретный пример голографии. Лучшее понимание этого могло бы привести к большему прогрессу в квантовой гравитации.

Выводы

Мы узнали, что законы физики, насколько мы их знаем, непоследовательны, так как мы не трактуем гравитацию квантовомеханически. Формулировка правильной теории квантовой гравитации дала бы нам возможность объяснить Большой Взрыв, и по всей вероятности, параметры Стандартной Модели.

Теория струн дает нам возможность изучить целый класс явлений, которых мы ожидаем в теории квантовой гравитации. Теория еще не разработана до той стадии, когда она могла бы давать определенные экспериментальные предсказания, но достаточно хорошо понята, чтобы объяснить некоторые квантовые явления гравитации, подобные энтропии и испарению черных дыр, изменению топологии и т.д. Суперсимметричные фазы теории струн исследуются довольно успешно.

Одна из главных задач - найти механизм, нарушающий суперсимметрию, который бы не порождал большой космологической постоянной. Было найдено много соответствий между различными теориями струн и между теорией струн и теорией поля. Показано, что теория струн приводит, в некоторых обстоятельствах, к обычной четырехмерной теории поля и наоборот. Мы надеемся, что в ближайшем будущем поймем теорию лучше, с тем чтобы вступить в непосредственный контакт с экспериментом.

Список литературы

1. J. Polchinski, String theory, Vol 1 and 2, Cambridge University press 1998.
2. M. Green, J. Schwarz and E. Witten, Superstring theory, Vol 1 and 2, Cambridge University Press 1987.
3. A. Strominger and C. Vafa, "Microscopic Origin of the Bekenstein-Hawking Entropy," Phys. Lett. B379, 99 (1996) [hep-th/9601029].
4. J. Maldacena, "The large N limit of superconformal field theories and supergrav- ity," Adv. Theor. Math. Phys. 2, 231 (1998) [hep-th/9711200].
5. S. S. Gubser, I. R. Klebanov and A. M. Polyakov, "Gauge theory correlators from non-critical string theory," Phys. Lett. B428, 105 (1998) [hep-th/9802109].
6. E. Witten, "Anti-de Sitter space, thermal phase transition, and confinement in gauge theories," Adv. Theor. Math. Phys. 2, 505 (1998) [hep-th/9803131].
7. 0. Aharony, S. S. Gubser, J. Maldacena, H. Ooguri and Y. Oz, "Large N field theories, string theory and gravity," hep-th/9905111.
8. G. 't Hooft, "A Planar Diagram Theory For Strong Interactions," Nucl. Phys. B72, 461 (1974).
9. N. Arkani-Hamed, S. Dimopoulos and G. Dvali, "The hierarchy problem and new dimensions at a millimeter," Phys. Lett. B429, 263 (1998) [hep-ph/9803315].
10. J. Polchinski, "Dirichlet-Branes and Ramond-Ramond Charges," Phys. Rev. Lett. 75, 4724 (1995) [hep-th/9510017].
11. E. Witten, "Anti-de Sitter space and holography," Adv. Theor. Math. Phys. 2, 253 (1998) [hep-th/9802150],
12. L. Susskind, "The World as a hologram," J. Math. Phys. 36 (1995) 6377 [hep- th/9409089],
13. G. 't Hooft, "Dimensional reduction in quantum gravity," gr-qc/9310026

Перевод осуществил В.О. Соловьев.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.