Исследованы процессы образования первичных черных дыр и аккреции материи на уже образованные первичные черные дыры. Даются ограничения на возможное число первичных черных дыр различной массы, выведенные из астрофизических наблюдений.

Введение

Кажется вероятным, что на очень ранних стадиях расширения Вселенной образовывались первичные черные дыры (PBH). Действительно, сейчас Вселенная очень однородна и изотропна на масштабах порядка космологического горизонта. В то же время, Вселенная имеет хорошо развитую структуру на масштабе галактик и меньших образований. Галактики кажутся образованными при росте малых неоднородностей вследствие гравитационной неустойчивости. В таком случае теория требует существования малых, но конечных возмущений фридмановской метрики с амплитудами порядка 0.01, содержащих примерно то же число барионов, что и современные галактики, в начале расширения Вселенной вблизи космологической сингулярности. Естественно предположить, что амплитуда возмущений на меньших масштабах будет еще большей. На том масштабе, где амплитуда возмущений была порядка единицы, мог имть место гравитационный коллапс первичной материи, когда космологический горизонт оказывался порядка масштаба возмущений. Именно таким образом могли быть образованы первичные черные дыры с массами от массы Планка и выше.

Возможность образования первичных черных дыр была упомянута в 1966 г. Зельдовичем и Новиковым и в 1971 г. Хокингом. Позже проблема PBH рассматривалась во многих статьях. Первичные черные дыры стали предметом значительного интереса с тех пор как Хокингом (1974, 1975а) было открыто квантовое испарение черных дыр малой массы, поскольку только первичные черные дыры могут обладать такими малыми массами. Процесс Хокинга является существенным для физики ранних стадий расширения Вселенной с одной стороны и как возможный путь регистрации первичных черных дыр во Вселенной с другой стороны. В этой статье обсуждается проблема образования PBH и аккреции материи на них на ранних стадиях эволюции Вселенной, а также связанный с этим процесс роста их масс; особое внимание будет уделяться ограничениям на возможное число первичных черных дыр различных масс, следующим из астрофизических наблюдений.

Образование первичных черных дыр

1. Каковы отклонения от космологической модели Фридмана в начале расширения, ведущие к образованию PBH?
2. Как происходит аккреция окружающей материи на уже образовавшуюся первичную черную дыру?

Обе проблемы были сформулированы и проанализированы в первых статьях по PBH (Зельдович, Новиков, 1966, 1967). Оказалось, что только численные расчеты могут дать исчерпывающий ответ на оба вопроса.

Соответствующие вычисления, проделанные Надеиным и др. (1977, 1978), показывают гидродинамическую картину образования PBH и последующей аккреции non-steady газа при простейшем предположении о сферической симметрии рассматриваемого процесса.

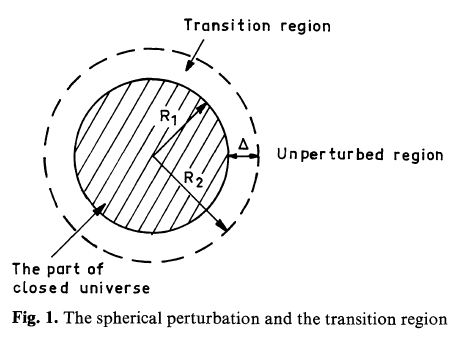
Зависимость процесса образования PBH от амплитуды отклонения от плоской модели Фридмана вблизи сингулярности (начала расширения) и от профиля этого отклонения (albeit в пределах предположения о сферической симметрии) также обсуждается в этой работе. Возмущение метрики вблизи сингулярности рассматривается как сферическая область с сопутствующим 3-пространством постоянной положительной кривизны, то есть, возмущенная область соответствует некоторой части замкнутой модели Фридмана. Амплитуда отклонения может быть характеризована числом, измеряющим вырезанную долю замкнутого пространства положительной кривизны. Эта часть замкнутой Вселенной сшивается с плоской моделью Фридмана через переходную область. Ширина последней, согласно нашим расчетам, является вторым важным параметром задачи.

Предполагается также, что вне возмущенной области решеник точно совпадает с плоской моделью Фридмана. Следовательно, возмущение таково, что полная масса вещества внутри возмущенной области в точности такая же какой она бы была в этой области в случае невозмущенной модели Фридмана.

Метрика пространства-времени дается формулой $$ds^2=c^2e^{\sigma}dt^2-e^{\omega}dR^2-r^2(d\theta^2+\sin^2\theta d\phi^2)$$ Выбрана сопутствующая система координат, $R$ -- лагранжев радиус частиц. Уравнение состояния материи $P=\varepsilon/3$. Невозмущенная метрика описывается следующей формулой $$ds^2=c^2dt^2-a(t)\left[ dR^2+ R^2(d\theta^2+\sin^2\theta d\phi^2)\right ]$$ Отклонения от этой формулы характеризуют возмущения метрики. Вблизи сингулярности в возмущенной области мы полагаем метрику следующей: $$ds^2=c^2dt^2-a(t)\left[ dR^2+ R^2(d\theta^2+\sin^2\theta d\phi^2) \right ]$$ Следовательно, амплитуда возмущения может быть описана с помощью $R_1$ -- величины $R$ на границе возмущенной области 3-пространства постоянной положительной кривизны (см. Рис. 1). Далее, переходная область простирается в интервале $$R_1< R< R_2,~~~R_2-R_1=\Delta$$ где решение постепенно сшивается с внешней невозмущенной областью. Развитие процесса существенно зависит от ширины переходной области. Действительно, если $\Delta$ достаточно мало, при возрастании возмущений плотности $\delta\rho$ развиваются крутые градиенты давлений и бурные гидродинамические явления. Если $\Delta$ велико, то градиенты давлений малы.

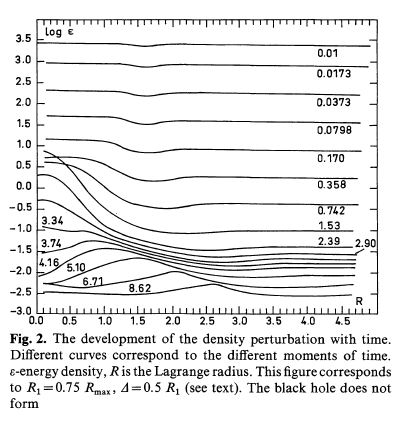
На Рис.2-4 показаны результаты вычислений (Надеин и др., 1978).

Если возмущения метрики малы (малое $R_1=0.75R_{max}$, где $R_{max}=\pi/2$, Рис.2), первоначальное возмущение плотности превращается в звуковую волну, распространяющуюся к бесконечности, и черной дыры не образуется. Для больших $R_1=0.80R_{max}$ возмущения плотности велики, но первичные черные дыры все же не образуются, возмущение распространяется в виде волнового пакета.

Для $R_1=0.9R_{max}$, $\Delta=0.5R_1$ (Рис.3,4) образуется PBH. На Рис.5 изображена кривая, показывающая при каких $R_1$ и $\Delta$ образуется первичная черная дыра, а при каких -- нет, а первоначальные возмущения становятся звуковыми волнами. Можно сделать следующие выводы. PBH могут возникнуть только при очень больших отклонениях от модели Фридмана, соответствующих $R_1\approx 0.85-0.9R_{max}$.

Ширина переходной области оказывает сильное влияние на образование PBH. Чем уже $\Delta$, тем больше роль градиентов давления, препятствующих образованию PBH. До того, как были сделаны числовые расчеты, делались попытки оценить важность давления при образовании PBH при помощи steady-state или само-подобных решений. Было сделано предположение, что давление может вносить вклад в аккрецию газа на PBH в процессе их образования и существенно увеличивать их массы. Carr и Hawking (1974) показали, что не существует самоподобного решения, приводящего к катастрофической аккреции материи на PBH, когда ее размер растет столь же быстро как космологический горизонт. Наши расчеты показывают, чтов действительности давление сильно препятствует образованию PBH, делая их массы меньше, чем они могли бы быть при том же начальном возмущении, но без давления $P=0$.

Действительно, вблизи сингулярности в пределах пространственного сечения $t=const$ плотность энергии в возмущенной области $R< R_1$ выше, чем вдали от центра в плоской модели Фридмана, и направленный вовне градиент давления при $R_1$ стремится отбросить материю прочь. В переходной области $\Delta$ плотность $\rho$ минимальна, и на внешней границе области $R_2$ направленный внутрь градиент давления порождает аккрецию.

Однако этот эффект менее значим для образования PBH, чем вышеупомянутый градиент при $R_1$, который приводит к истечению материи из возмущенной области. В результате масса PBH, которая в действительности образуется, составляет лишь $0.2-0.3$ от PBH, которая образовалась бы при полном отсутствии истечения, то есть, в случае $P=0$. Надо подчеркнуть, что размер PBH сразу после ее образования намного меньше космологического горизонта.

Когда образуется PBH, ее масса составляет около $0.01-0.06$ от массы, захваченной сферой с радиусом, равным космологическому горизонту. При таких условиях аккреция на PBH замедлена и лишь слегка увеличивает массу PBH при последующей эволюции. Наши расчеты это ясно показывают. Это заключение было доказано для само-подобных решений (Carr, Hawking, 1974) [и было упомянуто в качестве одной из возможностей Зельдовичем и Новиковым (1968)].

Многие другие интересные гидродинамические явления возникают в ходе образования PBH. Например, если принять переходную область очень узкой, тогда возникают ударные волны (см. Надеин и др., 1978). В случае низкого давления приливные взаимодействия разрушают сферическую симметрию и предотвращают образование PBH для малых возмущений.

Верхние пределы на спектр масс PBH

Другой подход к проблеме первичных черных дыр состоит в определении верхних пределов для спектра масс PBH на основе различных наблюдательных данных или космологических следствий их существования. Спектр масс PBH представляет большой интерес не только сам по себе, он также однозначно связан с первоначальным спектром адиабатических возмущений при $t=t_{pl}$, где $t_{pl}\approx 10^{-43}$ с (см. более детальные формулы у Carr, 1975). Каким путем могут быть открыты первичные черные дыры? Те, которые имеют массы $M>10^{15}$ г, однажды образовавшись, не слишком изменились к настоящему этапу развития Вселенной. Их потеря массы, вызванная квантовыми эффектами, мала, а рост массы благодаря аккреции вряд ли может быть существенным, как было показано выше.

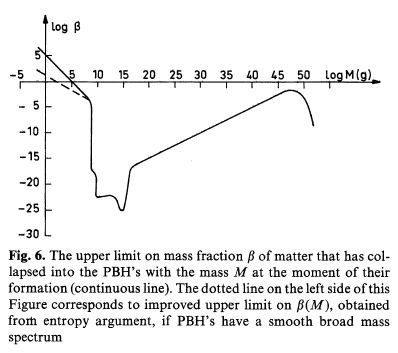
Такие PBH могут быть открыты только благодаря их гравитационному притяжению. В настоящее время вклад PBH в полную космологическую плотность энергии не может существенно превышать критической плотности, $\rho_{crit}\approx 5\cdot 10^{-30}$ г см$^{-3}$ ($H/50$ км с$^{-1}$ Мпс$^{-1}$)$^2$. Как было впервые показано Зельдовичем и Новиковым (1966), это условие налагает очень сильное ограничение на $\varepsilon_{PBH}$ в момент их образования. Этот момент $T_0$ зависит от массы PBH: Причиной этого является то, что при когда Вселенная расширяется согласно закону , плотность энергии излучения убывает как, тогда как (из-за космологического расширения скорость PBH быстро убывает, следовательно, эффективным уравнением состояния для PBH является $P=0$). Будем характеризовать спектр PBH в момент их образования величиной $\beta(M)=(\varepsilon_{PBH}/\varepsilon_m)_{t=t_0}$, где $\varepsilon_{PBH}(M)$ -- плотность энергии PBH с типичными массами отдельной PBH порядка $M$, $\varepsilon_m$ -- полная плотность энергии излучения и вещества для $\Omega=1$ (если $\beta(M)\ll1$), то $\varepsilon_m\sim 1/Gt^2$). Здесь мы предполагем, что основная часть PBH сконцентрировано вблизи одного значения массы $M$. В случае широкого спектра PBH его амплитуда должна характеризоваться производной $d\beta/dM$.

Величина $\beta(M)$ представляет всю ту долю материи, которая коллапсировала в первичные черные дыры, имевшие массу $M$ в момент их образования. Сплошная кривая на Рис.6 представляет верхний предел на $\beta(M)$ для случая $\Omega_m=0.1$. Верхний предел на $\beta(M)$ в интервале $10^{16}$ g$< M < 10^{48}$ г следует из приведенного выше аргумента (Зельдович, Новиков, 1966) и дается неравенством $\beta(M)\lesssim 10^{-25}M^{1/2}$ г. Для $M>10^{15}M_\odot \approx 10^{48}$ г верхний предел на $\beta(M)$ и $\varepsilon_{PBH}$ может быть существенно улучшен на основе отсутствия 24-часовой крупномасштабной анизотропии в реликтовом фоновом излучении\footnote{Если бы существовали столь большие черные дыры, мы должны были бы падать в гравитационном поле ближайшей из них и должны были бы наблюдать анизотропию в реликтовом фоновом излучении}.

Другие способы установить верхний предел на $\beta$ для $M>10^{15}$ г обсуждаются в работе (Carr, 1975) (см. также недавний обзор Carr, 1978), но они не слишком сильно изменяют полученные выше результаты. Ситуация резко меняется в случае PBH с массами меньше чем $10^{15}$ г, так как, в результате эффекта испарения черных дыр, открытого Хокингом (1975), такие PBH уже испарились к настоящему времени. При испарении PBH испускают частицы и античастицы с характерными энергиями $E\approx 4-6\ T_{BH}$, где $T_{BH}=\hbar c^3/8\pi GM\approx 10^{13}/M$(г) ГэВ (для шварцшильдовской черной дыры). Время жизни PBH $t_1$ зависит от ее массы и имеет порядок $10^{-27}\ M^3$(г) с. Здесь мы предполагаем картину Элементарной Частицы (а не картину Составной Частицы) при числе различных типов ``истинно элементарных частиц'' приближающемся к 20-30; это подразумевает, чтоуравнение состояния в ранней Вселенной имеет вид $P_m=\varepsilon_m/3$.

Введем величину $\alpha(M)=(\varepsilon_{PBH}/\varepsilon_m)_{t=t_1(M),\Omega=1}$ (то есть, в момент полного испарения PBH с массой $M$). Если $\alpha(M)< 1$, то $\beta$ связана с $\alpha$ соотношением где $M_{pl}=2\cdot 10^{-5}$ г. После завершения испарения PBH плотность рожденных частиц будет где $n_m$ -- полная плотность числа частиц, а $n_B$ -- плотность барионного числа в момент времени $t_1$ ($t_1$ в секундах)\footnote{Предполагаемое значение постоянной Хаббла 50 км с$^{-1}$ Мпс$^{-1}$}. При $t_1\gtrsim 1$ с главный вклад в $n_m$ дают безмассовые частицы и (при $t_1 < 10$ с) $e^+e^-$-пары. Как подсчитано (Page, 1976) 45\% энергии, испущенной PBH с массой $5\cdot 10^{14}$ g $< M<10^{17}$ г, находится в виде релятивистских электронов и позитронов, 45\% - в виде нейтрино, 9\% - в фотонах и 1\% - в гравитонах. PBH с меньшими массами испускают также $\pi$-мезоны, нуклоны и другие сильновзаимодействующие частицы.

Верхние пределы на $\varepsilon_{PBH}(M)$ с массами $M\sim 10^{14}-10^{15}$ г, испаряющиеся после рекомбинации, были получены в работах Chapline (1975), Page, Hawking (1976), Carr (1976). Наиболее сильное ограничение было получено для PBH с массами $M\sim 10^{15}$ г из наблюдений $\gamma$-излучения (в предположении, что отсутствует кластеризация PBH в галактических гало). Полная плотность $\gamma$-излучения, испущенного этими PBH не должно превышать наблюдаемой плотности $\gamma$-излучения косимческого фона. Этот предел есть $\alpha(10^{15}\ г)\lesssim 10^{-8}$, $\beta(10^{15}\ г)\lesssim 10^{-25}$. Многообещающий метод поиска PBH этой массы был недавно предложен в работе Rees (1977). Автор подчеркивает, что коллективные взаимодействия электронов и позитронов, испущенных при конечном взрыве PBH, с межзвездным магнитным полем могут генерировать мгновенную вспышку в диапазоне радиоволн (см. также детальные расчеты этого процесса в работе Blanford, 1977).

Однако в настоящее время этот механизм может быть использован для улучшения вышеупомянутого предела только при дополнительных предположениях о кластеризации PBH в гало галактик и о значении межзвездного магнитного поля в окрестности PBH (см. результаты и дальнейшие перспективы в работе Meikle, 1977). Кроме того, сильное ограничение на спектр PBH в области масс $10^{13}$ g $< M< 10^{14}$ г следует из рассмотрения влияния высокотемпературного излучения PBH на кинетику рекомбинации (Насельский, 1978).

PBH в диапазоне масс $10^{11}$ g $< M< 10^{13}$ г испаряются до рекомбинации, но испущенное излучение не достигает состояния равновесного распределения, поскольку плотности чисел барионов и электронов малы и bremsstrahlung не может дать достаточного числа фотонов в области спектра Рэлея-Джинса (детали см. Сюняев, Зельдович, 1970; Илларионов, Сюняев, 1974, где исследован случай произвольного источника энергии). Таким образом, испущенные фотоны должны искажать спектр фонового излучения.

Сравнение с наблюдаемым спектром фонового электромагнитного излучения показывает, что в обсуждаемой области масс $\alpha(M)<10^{-2}-1$, $\beta(M)M/M_{pl}<10^{-2}-1$ (Зельдович, Старобинский, 1976). Некоторые ограничения сверху на $\varepsilon_{PBH}$ в области масс $10^{9}$ g $< M<10^{12}$ г могут быть получены, если принять во внимание влияние испущенных PBH адронов высоких энергий (Зельдович и др., 1977) и нейтрино (Вайнер и Насельский, 1977) на нуклеосинтез гелия (Зельдович и др., 1977; Вайнер и Насельский, 1977) и дейтерия (Зельдович и др., 1977) в ранней Вселенной. Нетрудно проверить, что в принятой модели с ограниченным числом истинно элементарных частиц взаимодействие между частицами, испущенными единичной черной дырой достаточно малой массы несущественно, даже если эти частицы являются адронами. Действительно, если $T_{BH}\gg m_{p}$ (или массы кварка), все испускаемые частицы являются ультрарелятивистскими.

С другой стороны, частицы могут излучаться только одна за другой при характеристических интервалах $\Delta t=\delta^{-1}r_g/c$ при $\delta$ около $(2-4)\cdot 10^{-2}$, если основную долю излученных частиц составляют адроны и число элементарных адронов примерно 10-20. Из-за дискретности процесса излучения в момент рождения частица эффективно окружена вакуумной полостью размера около $\delta^{-1}r_g$ и при $r>\delta^{-1}r_g$ плотность числа ранее испущенных частиц есть $n(r)\approx \delta r_g^{-1}r^{-2}(4\pi)^{-1}$. Внутренняя граница полости расширяется с ультрарелятивистской скоростью. Принимая во внимание, что относительные скорости частиц в системе покоя PBH малы (порядка $cm_p^2/E^2$, где $E$ -- характеристическая энергия частиц, $E\sim (4-6)T_{BH}\gg m_p$) и предполагая сечение сильного взаимодействия близким к $(\hbar/m_\pi c)^2$, можно вычислить число столкновений любой испущенной частицы со всеми остальными частицами, излученными той же самой черной дырой.

Оно оказывается $\nu=4\pi\delta^2(m_p/m_\pi)^2(m_pT_{BH}/E^2)<1$, если $T_{BH}>m_p$. Таким образом, малые PBH впрыскивают нуклоны высоких энергий в окружающее пространство. Антинуклоны, испущенные PBH с массами $M\sim 10^9-10^{10}$ г ($t_1\sim 1-10^3$ с) аннигилируют с фоновыми нуклонами и увеличивают отношение числа нейтронов к числу протонов в фоновом веществе без изменения плотности полного барионного числа $n_p+n_n$, поскольку излучение ЧД симметрично по отношению к барионному заряду с точностью до несущественных статистических флуктуаций [если нет специального механизма, связанного с CP-нарушением (Hawking, 1975b; Зельдович, 1976)]. Это приводит к возрастанию доли первичного $\mathrm{He}^4$. Тогда из сравнения с наблюдаемой долей $\mathrm{He}^4$ (доля массы $Y_{\mathrm{He}^4}< 30\%$) можно получить следующий предел: $$ \alpha(M)<10^{-2}t_1^{1/6}\Omega, $$ для $10^9\ g< M<10^{10}$g ($t_1$ здесь и ниже выражено в секундах).

Ограничения на спектр PBH, полученные из рассмотрения влияния нейтрино $\nu_e$ и антинейтрино $\bar\nu_{\bar e}$ высоких энергий, испущенных PBH на отношение $n/p$ и нуклеосинтез $\mathrm{He}^4$, примерно в $10^3$ раз слабее, если $\Omega=0.1$. Сильное ограничение на $\varepsilon_{PBH}$ в области $10^{10}\ г< M< 10^{13}$ г может быть получено из распространенности дейтерия. В этом случае наиболее интересный для нас процесс --- это spallation ядер первичного $\mathrm{He}^4$ ультрарелятивистскими нуклонами и антинуклонами, испущенными PBH. Нейтроны, рожденные этим процессом (а также первоначально испущенные PBH), быстро захватываются фоновыми протонами, образуя ядра дейтерия.

Средняя длина свободного пробега $h$ до образования $D$ меньше, чем $c\times$[время жизни нейтрона $\sim 10^3$ с], если $t_1<10^5\Omega^{2/3}$ с. Дейтерий не сжигается в достаточных количествах в реакциях $D+D\rightarrow T+p$ или $D+D\rightarrow \mathrm{He}^4+n$, если $t_1>3\cdot 10^3\ с\ (\Omega=1)$ или $t_1>\cdot 10^3\ с\ (\Omega=0.1)$ Так как $Y_D$ не может превышать $5\cdot 10^{-5}$, мы получаем следующий верхний предел на $\alpha$ в интервале $10^{10}$ g $< M<5\cdot 10^{10}$ г (Зельдович и др., 1977): $$ \alpha\lesssim 10^{-6}t_1^{1/6}\Omega. $$ В частности, если $M\sim 10^{10}$ г и $\Omega=0.1$, тогда $\beta<5\cdot 10^{-22}$. Если $t_1>10^5$ с, основной вклад в обсуждаемый эффект происходит из реакции прямого рождения дейтерия в spallation $\mathrm{He}^4$. Известно, что доля этой реакции составляет примерно 25\% при $E\gtrsim 1$ Гэв.

Характерное время соударения между нуклонами и антинуклонами, испущенными PBH и фоновыми ядрами $\mathrm{He}^4$ меньше, чем горизонт, даже если $M\sim 10^{13}$ г ($t_1\sim 10^{12}$ с). Это приводит к пределу на $\alpha$ в области $10^{11}\ г< M< 10^{13}$ г: $$ \alpha<5\cdot 10^{-6}t_1^{1/6}\Omega. $$ Таким образом, первичное содержание дейтерия есть очень чувствительный индикатор PBH. Важно подчеркнуть другую сторону этого результата. Хорошо известно, что наблюдаемое содержание дейтерия трудно объяснить в рамках обычной схемы нуклеосинтеза, если принимать высокую плотность вещества во Вселенной [$\rho>6\cdot 10^{-31}\ г/см^3$, $\Omega>0.1$ или $\Omega>0.5$ в случае сильной, специально созданной неоднородности (Wagoner, 1973; Зельдович, 1975)].

Из результатов, полученных выше, следует, что присутствие небольшого числа ($\beta\sim 10^{-20}$) черных дыр с $M\sim 10^{10}-10^{12}$ г дает нам уникальную возможность объяснить наблюдаемое содержание дейтерия даже если $\Omega=1$. И из-за этого практически ни одно другое свойство Вселенной не изменится.

В частности, при $\Omega>0.1$ предлагаемый механизм дает небольшое увеличение содержания $\mathrm{He}^3$: $Y_{\mathrm{He}^3}\sim (1-3)\cdot 10^{-5}$, которое не противоречит наблюдательным данным (принимая во внимание возможность разрушения $\mathrm{He}^3$ в звездах). $\mathrm{He}^3$ образуется и прямо в процессе spallation $\mathrm{He}^4$ и из дейтерия в реакции $D+D\rightarrow \mathrm{He}^3+n$. Содержание $\mathrm{He}^3$, рожденного таким способом, никогда не превысит содержания дейтерия. Предложенный механизм не приводит к возрастанию содержания $\mathrm{Li}^7$. Следует здесь заметить, чтосогласно расчетам (Wagoner) содержание $\mathrm{Li}^7$, образованного в ранней фридмановской Вселенной (без PBH), с $\Omega>0.1-0.2$ согласуется с наблюдениями. Существенно, что предложенный механизм не сталкивается с двумя главными трудностями характерными для всех ранее предложенных механизмов рождения дейтерия. Этими трудностями являются (см. например Epstein et al., 1976; Epstein, 1977): а) перепроизводство $\mathrm{Li}^6$ и $\mathrm{Li}^7$, а также $\mathrm{B}^{11}$; б) перепроизводство $\gamma$-излучения.

Первая трудность не возникает, поскольку, с одной сороны, частицы, испущенные PBH имеют очень высокие характерные энергии $E\sim 50-5000$ Гэв в интервале масс PBH $10^{10}\ г\gtrsim M\lesssim 10^{12}$ г (и поэтому сечения образования $\mathrm{Li}^6$ и $\mathrm{Li}^7$ очень малы) и с другой стороны, доля $\alpha$ (и $\bar\alpha$)частиц в излучении PBH исключительно мала (именно в столкновениях $\alpha+\mathrm{He}^4$ образуются ядра $\mathrm{Li}$). Скорость образования $\mathrm{B}^{11}$ в этой модели даже ниже, чем обычно. Вторая трудность не возникает, поскольку у $\gamma$-излучения, возникшего при spallation $\mathrm{He}^4$ имеется достаточно времени для поглощения веществом в ходе дальнейшей эволюции Вселенной.

Если $M_{PBH}< 10^9$ г ($t_1 < 1$ с), то излучение PBH быстро термализуется и удельная энтропия Вселенной (на барион) $S$ возрастает. Таким образом, верхние пределы на $\alpha(M)$ для $M< 10^9$ г могут быть получены путем сравнения накопленного количества энтропии с величиной, измеренной в настоящее время $S\approx 10^9/\Omega$ $(H/50\ км\ с^{-1}\ Мпс^{-1})^2$, где вклад от реликтовоых термальных $\nu_e$, $\bar\nu_e$ и $\nu_\mu$, $\bar\nu_\mu$ принят во внимание. Оказывается, что энтропия главным образом производится не в момент рождения частицы PBH, а в ходе последующей релаксации и термализации этих частиц. Вычисления показывают (Zeldovich and Starobinsky, 1976), что если большинство PBH имеет типичную массу M, то удельная энтропия после релаксации будет $$ S=(1+S_0)\beta M/M_{pl} $$ где $S_0$ -- начальная удельная энтропия до испарения PBH. Отсюда следует, что $\beta\lesssim (10^9/\Omega)(M_{pl}/M)$.

В частности, вся энтропия, наблюдаемая в настоящее время, может быть результатом испарения PBH; чтобы это имело место, достаточно, например, чтобы половина вещества в первоначально холодной Вселенной ($S_0\ll1$) коллапсировала в PBH с $M\sim 10^4/\Omega$(г). Заметим, что даже если $\beta(M)<1$ в этом случае позже будет стадия эволюции с $\varepsilon_{PBH}\gg\varepsilon_m$ и закон расширения $a(t)\sim t^{2/3}$. Если $M<10^4/\Omega$ (г), тогда возможно $\beta(M)>l$. Если PBH не концентрируются вблизи некоторой одной массы, а имеют широкий спектр масс, тогда верхний предел на $\beta(M)$, полученный из рассуждений об энтропии, может быть улучшен (см. пунктирную линию слева на Рис. 6).

Предположим, например, что спектр масс PBH имеет вид $d\beta(M)/dM=\gamma/M$ в интервале $M_{pl} < M < M_{max}$, где $\gamma=\mathrm{const}<1$. Этот спектр соответствует плоскому спектру начальных адиабатических возмущений метрики при $t=t_{pl}$. Тогда верхний предел для $\gamma$ оказывается $\gamma^2(M/М_{рl})^{4/3}<10^9/\Omega$, при $10^4$ g $

При получении следующего ограничения существенным предположением было, что черные дыры не оставляют после себя никаких остатков, хотя теория рождения пар в гравитационном поле черной дыры, трактуемой классически, применима лишь при $M>M_{pl}\approx 2\cdot 10^{-5}$ г. Если предположить, что черные дыры испаряются только до массы $M_{pl}$, а потом испарение каким-либо образом останавливается, то мы должны получить очень сильные ограничения на верхние пределы $\beta(M)$ при $M<10^{9}$ g: $\beta < 10^{-20}M^{3/2}(g)$. Этот предел следует из аргументов о возрасте Вселенной и он такой же как для PBH с массой в интервале $10^{16}g< M< 10^{48}$ г. В частности, $\beta(M) < 10^{-27.5}$ при $M\sim 10^{-5}$ г соответствует среднеквадратичной амплитуде возмущений метрики $h < 0.03$ на масштабе $10^{-33}$ см (если предполагается гауссово распределение для возмущений и уравнение состояния $P=\varepsilon/3$). Следовательно, космологические аргументы указывают, что или черные дыры испаряются полностью, или флуктуации метрики на масштабе $10^{-33}$ см существенно меньше единицы.

Заключение

Обе проблемы были сформулированы и проанализированы в первых статьях по PBH (Зельдович, Новиков, 1966, 1967). Оказалось, что только численные расчеты могут дать исчерпывающий ответ на оба вопроса.(Помимо PBH в литературе обсуждаются также белые дыры. Было показано, что квантовые эффекты вблизи сингулярности (Зельдович и др., 1974) как и аккреция (Eardley, 1974) существенны для белых дыр, благодаря чему они быстро становятся разновидностью черных дыр.)

Соответствующие вычисления, проделанные Надеиным и др. (1977, 1978), показывают гидродинамическую картину образования PBH и последующей аккреции non-steady газа при простейшем предположении о сферической симметрии рассматриваемого процесса. Зависимость процесса образования PBH от амплитуды отклонения от плоской модели Фридмана вблизи сингулярности (начала расширения) и от профиля этого отклонения (albeit в пределах предположения о сферической симметрии) также обсуждается в этой работе. Возмущение метрики вблизи сингулярности рассматривается как сферическая область с сопутствующим 3-пространством постоянной положительной кривизны, то есть, возмущенная область соответствует некоторой части замкнутой модели Фридмана. Амплитуда отклонения может быть характеризована числом, измеряющим вырезанную долю замкнутого пространства положительной кривизны. Эта часть замкнутой Вселенной сшивается с плоской моделью Фридмана через переходную область. Ширина последней, согласно нашим расчетам, является вторым важным параметром задачи.

Новиков И.Д., Полнарев А.Г., Старобинский А.А., Зельдович Я.Б.

Перевод осуществил В.О. Соловьев.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.