Проблема космологической постоянной
Вакуум — это самый загадочный объект, с которым когда-ли-бо встречались физики. А самый страшный секрет вакуума — это происхождение его энергии. Я должен подчеркнуть, что говорю не о высокоэнергичном вакууме инфляционной космологии. Как раз физика ложного вакуума относительно понятна. Загадочный объект, о котором идет речь, — это обычный, истинный вакуум, в котором мы сейчас обитаем.
Немногие теоретические оценки в истории физики...
были настолько неточными.
Ларри Эббот
Кризис энергии вакуума
Вакуум — это то, что остается, когда мы убираем все частицы и излучение. Для классического физика это просто пустое пространство, и о нем нечего больше сказать. Но в квантовой физике вакуум — это арена безумно активной деятельности.
Возьмем, к примеру, электромагнитное излучение. Оно состоит из фотонов — небольших сгущений электромагнитной энергии. Допустим, у нас есть ящик чистого вакуума. Мы напрочь опустошили его и убедились, что внутри не осталось ни одного фотона, ни одной частицы. Можно предположить, что электрическое и магнитное поля в ящике должны быть строго равны нулю. Но это не так. Квантовый вакуум отказывается пребывать в покое. Точно так же, как скалярное поле во время инфляции, электрическое и магнитное поля испытывают случайные рывки или квантовые флуктуации.
Если вы попробуете измерить, скажем, магнитное поле внутри ящика, полученный результат будет зависеть от размера вашего измерительного устройства. Предположим, для начала вы взяли относительно крупное приспособление, измеряющее поле в масштабе 1 сантиметр. Тогда величина измеренного поля составит несколько миллиардных долей гаусса. (Для сравнения: напряженность магнитного поля Земли составляет у поверхности около 1 гаусса.) Спустя одну наносекунду направление поля станет совершенно другим, но его величина останется где-то между нулем и несколькими миллиардными гаусса. Чтобы заметить эти стремительные флуктуации поля, измерения надо выполнять быстро. Если измерение занимает больше наносекунды, вы получите среднее значение поля, которое будет очень близко к нулю.
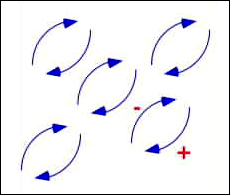
Детектор размером 1 миллиметр зарегистрирует в 100 раз более сильное поле, которое флуктуирует в 10 раз быстрее. Эти соотношения сохраняются по мере дальнейшего уменьшения масштабов: каждый раз, когда вы уменьшаете масштаб длины в 10 раз, величина флуктуации увеличивается в 100 раз, а их частота возрастает десятикратно. В масштабе атомов флуктуирующее магнитное поле в 10 миллионов гаусс меняет свое направление примерно $10^{17}$ раз в секунду.
Мы не замечаем этих колоссальных магнитных полей, потому что они очень быстро меняются отточки к точке и от мгновения к мгновению. Стрелка компаса, например, реагирует на магнитное поле, осредненное по всей ее длине, и за интервал времени, достаточный для существенного ее поворота (скажем, 0.1 секунды). Влияние квантовых флуктуации на таких масштабах совершенно ничтожно.
Все это замечательно, пока мы не заинтересуемся энергией флуктуации. Плотность энергии магнитного поля зависит только от его напряженности, но не от направления. Поэтому, даже если поле колеблется в разные стороны, его плотность энергии в среднем не равна нулю. Сильные, быстро флуктуирующие поля на малых расстояниях вносят большой вклад в плотность энергии, и тут мы сталкиваемся с серьезной проблемой. По мере рассмотрения все меньших и меньших размеров плотность энергии неограниченно возрастает. В результате мы приходим к абсурдному выводу, будто плотность энергии вакуума бесконечна! Похоже, в нашей теории что-то глубоко неверно. Попробуем разобраться, что бы это могло быть и как нам обойти этот странный результат.
Бесконечность возникает, если мы допускаем, что линейный масштаб флуктуации может быть сколь угодно малым. Но ведь не исключено, что существует предел тому, насколько малыми они могут быть. На сверхмалых расстояниях геометрия пространства и времени тоже оказывается подвержена большим квантовым флуктуациям. Как и в случае электромагнетизма, чем меньше линейный масштаб, тем больше флуктуации. Ниже некоторого критического размера, называемого планковской длиной, пространство время обретает хаотическую, пенообразную струкутуру. Пространство неистово закручивается и сминается, крошечные "пузырьки" отрываются от него и немедленно коллапсируют, возникает и мгновенно исчезает множество "ручек" или "туннелей" (рис. 12.1). Планковская Длина невероятно мала: она составляет одну миллиардно-триллионно-триллионную долю сантиметра. В значительно больших масштабах пространство выглядит гладким, а "пространственно-временная пена" не видна — подобно тому как пенная поверхность океана кажется гладкой, если смотреть на нее с большой высоты.
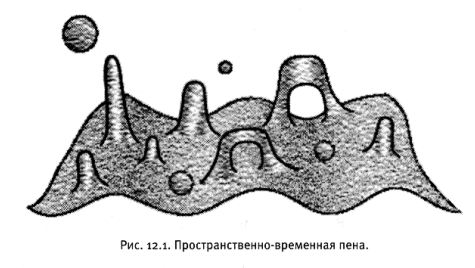
Возможно, столь резкое изменение свойств пространства-времени гасит идущие вразнос электромагнитные флуктуации. Этого нельзя сказать с уверенностью, поскольку физика пространственно-временной пены не вполне ясна. Но даже при наилучшем раскладе ничто не ограничивает флуктуации в масштабах, больших, чем планковская длина. Оценка плотности энергии таких флуктуации дает поразительную величину $10^{88}$ тонн на кубический сантиметр, что намного превосходит энергию вакуума Великого объединения!
Количественные и концептуальные проблемы, с которыми сталкивается СКМ при описании динамики Вселенной, не может оставить равнодушным ни одного физика (согласно А. Эйнштейну, ''высшим долгом физиков является поиск тех общих, элементарных законов, из которых путём чистой дедукции можно получить картину Мира'').
Одной из наиболее важных проблем в космологии, да и вообще в физике, является отличие наблюдаемой плотности космологической постоянной от теоретически ожидаемой на $120$ порядков.
В физике частиц космологическая постоянная естественно возникает как плотность энергии вакуума, которая может быть оценена как сумма нулевых колебаний квантовых полей с массой $m$.
Таким образом, можно записать \begin{equation} \rho_{vac}=\frac{1}{2}\int_{0}^{\infty }\frac{d\vec{k}}{(2\pi)^3}\sqrt{k^2+m^2}\approx\frac{1}{4\pi^2}\int_{0}^{\Lambda }k^2dk\sqrt{k^2+m^2} \end{equation} \begin{equation} \label{rho_{vac}} \rho_{vac}\approx \frac{\Lambda^4}{16\pi^2} \end{equation}
Согласно идеологии КТП, для оценки плотности энергии космологической постоянной, отождествлённой с плотностью энергии физического вакуума при интегрировании разумно выбрать следующее ограничение: \begin{equation} \Lambda \sim M_{Pl}, \end{equation} где \begin{equation} M_P=\left( \frac{1}{8\pi G} \right)^{1/2}=\left( \frac{1}{8\pi }\frac{\hbar c}{G} \right)^{1/2}\sim 10^{18}\; GeV={{10}^{-5}}g. \end{equation} Соотношение $ \Lambda \sim M_{Pl}$ называется ультрафиолетовым обрезанием (UV cutoff). Плотность физического вакуума, к которой приводит такой выбор $\Lambda$ равна \begin{equation} \rho_{vac}\approx 10^{74} \;GeV^4 \end{equation} Что как и обещалось на $120$ порядков превышает её наблюдаемое значение: \begin{equation} \label{rho_{vacObs}} \rho_{vac}\approx 3\cdot 10^{-47} \;GeV^4 \end{equation}
Плотность энергии истинного вакуума — это то, что Эйнштейн называл космологической постоянной. Если она действительно так невероятно велика, Вселенная должна сейчас находиться в состоянии взрывного инфляционного расширения. Однако наблюдаемый темп расширения Вселенной ограничивает величину космологической постоянной значением в $10^{120}$ (это больше гугола!) раз меньшим. Итак, мы столкнулись с задкой: почему плотность энергии вакуума не так велика? Столь разительное несоответствие между предсказанным и наблюдаемым значениями космологической постоянной известно под названием проблемы космологической постоянной. Это одна из самых волнующих и будоражащих ум загадок в теоретической физике элементарных частиц.
В поисках глубинной симметрии
Помимо электромагнетизма квантовые флуктуации других полей также вносят свой вклад в энергию вакуума. Некоторые из этих вкладов оказываются отрицательными, и это дает надежду на то, что положительные и отрицательные вклады в энергию скомпенсируют друг друга. Эта возможность стимулировала многочисленные попытки решения проблемы космологической постоянной.
Все элементарные частицы делятся на два типа: бозоны и фермионы(Они называются в часть Шатьендраната Бозе и Эрнико Ферми, которые сформулировали их отличительные свойства.). Фотоны, например, относятся к бозонам, а электроны, позитроны, кварки — к фермионам. Ферми-частицы можно представлять в виде небольших сгущений фермионных полей, однако, в противоположность электромагнетизму, величины таких полей характеризуются так называемыми грассмановыми числами(Названы в честь немецкого математика XIX века Германа Грассмана, который ввел 'их в оборот), которые очень сильно отличаются от обычных. Когда вы перемножаете обычные числа, результат не зависит от порядка сомножителей; например, 4x6 = 6x4 = 24. Однако произведение грассмановых чисел при этом меняет знак: АхВ = -ВхА. Грассманов характер фермионных полей ответствен за многие особенности ферми-частиц, но для нас важно то, что вакуумные флуктуации ферми-полей имеют отрицательную плотность энергии.
Может ли положительная энергия бозе-полей быть скомпенсирована отрицательной энергией ферми-полей? В принципе это возможно, но выглядит крайне маловероятным. Огромные положительные и отрицательные члены уравнений, сложнейшим образом связанные с массами и взаимодействием частиц должны совпасть по величине с точностью лучше, чем единица к гуголу. С чего бы случиться такому чудесному совпадению?
Удивительные сокращения случаются в физике элементарных частиц, но они обычно связаны с некоторой лежащей в их основе симметрией. Возьмем, к примеру, сохранение электрического заряда. Высокоэнергичные столкновения могут порождать мириады новых частиц, но всегда можно быть уверенным, что число положительно и отрицательно заряженных среди них будет в точности равным, так что совокупный заряд останется неизменным. Это свойство связано с особой симметрией уравнений физики элементарных частиц, называемой калибровочной симметрией(Про уравнение говорят, что оно обладает симметрией, если существует некоторая операция, при которой оно остается неизменным. Например, уравнение х + у = 1 не меняется, если поменять местами х и у).
Из калибровочной симметрии следует, что электрический заряд сохраняется при любых взаимодействиях элементарных частиц. Красота симметрии состоит в том, что детали не имеют значения. Неважно, каковы массы частиц и в какие взаимодействия они друг с другом вступают. Сохранение заряда имеет место всегда.
Вплоть до самого недавнего времени абсолютное большинство физиков верило, что нечто подобное должно иметь место и в случае энергии вакуума. Должна существовать некая пока еще не открытая глубинная симметрия, которая приводит к сокращению различных вкладов в космологическую постоянную. Начиная с 1970-х годов при участии лучших умов было предпринято множество попыток разобраться, что это может
, за симметрия. Однако несколько десятилетий усилий так и не принесли значимых успехов. Проблема космологической постоянной остается столь же неприступной, как и прежде.
Проблема совпадения(Более подробно об этой проблеме)
"Любое совпадение, — сказала себе мисс Марпл, — это лучше, чем ничего. Если это просто совпадение, его потом можно отбросить".
Агата Кристи
Когда в конце 1990-х годов две группы астрономов сообщили, что обнаружили признаки далеко не исчезающе малой величины космологической постоянной, их заявление оказалось полнейшей неожиданностью. Как уже говорилось, это открытие стало важнейшим событием для теории инфляции. Плотность массы (энергии) вакуума оказалась в точности такой, какая требовалась, чтобы сделать Вселенную плоской. Но для физики элементарных частиц оно стало страшной неприятностью.
Шансы найти решение проблемы космологической постоянной становились теперь и вовсе ничтожными. Симметрия должна работать идеально; она не оставила бы и следа некомпенсированной энергии вакуума. И это еще не все. Фактическое значение космологической постоянной, полученное из новых данных, выглядело крайне подозрительно. Оно было настолько велико, что большинство физиков, занимающихся элементарными частицами, и космологов просто отказывались в него верить, надеясь, что как-нибудь все обойдется.
|
Наблюдаемая плотность массы вакуума оказалась примерно вдвое больше средней плотности вещества. Удивляло то, что эти две плотности сравнимы друг с другом по величине. Это было странно, поскольку плотность вещества и плотность вакуума совершенно по-разному ведут себя в ходе расширения Вселенной. Плотность вакуума остается совершенно неизменной (до тех пор, пока мы остаемся в том же самом вакууме), а плотность вещества убывает с ростом объема. Если эти две плотности сегодня примерно совпадают, значит, в эпоху последнего рассеяния вещество в миллиарды раз превосходило вакуум по плотности, а через секунду после Большого Взрыва она была в $10^{45}$ раз выше. В далеком будущем ситуация сменится на противоположную: плотность вещества станет много меньше, чем у вакуума. Например, через триллион лет она будет в $10^{50}$ раз меньше.
Именно это происходит в тех теориях элементарных частиц, где есть особый вид симметрии, называемый суперсимметрией. Бозоны и фермионы в таких теориях появляются парами, так что каждая бозе-частица имеет фермионного партнера и наоборот. Частицы-партнеры в каждой паре имеют одинаковую массу, а ваккумные энергии фермионов и бозонов в точности сокращаются. Поэтому полная плотность энергии вакуума равна нулю.
Это могло бы оказаться изящным решением проблемы космологической постоянной, но беда в том, что наш мир определенно не суперсимметричен. В противном случае на ускорителях наблюдалось бы рождение многочисленных партнеров электронов, кварков и фотонов. Кроме того, даже в суперсимметричном мире космологическая постоянная сокращается только в отсутствие гравитации. Если же принять ее в расчет, то энергия вакуума приобретает большое отрицательное значение.
Таким образом, на протяжении большей части истории Вселенной плотности вещества и вакуума очень сильно различались. Почему же в таком случае нам довелось жить именно в ту особенную эпоху, когда эти две плотности столь близки друг к другу? Если глядеть на огромный диапазон изменения плотности вещества, это совпадение выглядит таким странным, что его трудно считать "просто совпадением".
Похоже, будто Природа пыталась нам что-то сказать. Но, по своему обыкновению, она не озаботилась внятностью формулировки. Почему такая фундаментальная величина, как космологическая постоянная, должна быть связана с плотностью вещества в ту определенную эпоху, когда довелось появиться человеку? Сама мысль о связи этих двух величин выглядела совершенно вздорной. Сообщество физиков элементарных частиц пребывало в замешательстве.
И тогда обнаружился замечательный факт, сделавший ситуацию еще более странной. Ненулевое значение космологической постоянной, не очень далекое от наблюдаемого, как оказалось, было предсказано теоретически за много лет до упомянутых наблюдений. Правда, с этим предсказанием была связана одна проблема. Оно основывалось на так называемой антропной селекции — весьма неоднозначной идее, которой уважающие себя физики избегают как чумы.
Отрывок из книги А. Виленкина "Many Worlds in One: The Search for Other Universes"
Комментарии (4):
''высшим долгом физиков является поиск тех общих, элементарных законов, из которых путём чистой дедукции можно получить картину Мира''
Красивый математический эгоцентризм, но не более.
Напомню:
Нельзя абсолютно точно описать реальный обЪект конечным набором свойств_характеристик (это постулат).
Далее:
Картина МИРА не зависит от математики (от любого её раздела), но с помощью математики можно попытаться понять лишь некоторые свойства_факты Картины МИРА (причинная зависимость в суждениях!!!).
Да, так что вам не понравилась в высказывании А. Эйнштейна:
''высшим долгом физиков является поиск тех общих, элементарных законов, из которых путём чистой дедукции можно получить картину Мира''
К den [21 April, 23:37]
А кто сказал что мне что-то не понравилось?
Я лишь заострил самоё понятие долга физиков.
Оно (это понятие долга) эквивалентно утверждению:
Жизнь прекрасна во всех её проявлениях.
Не так ли?
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.