От космологической модели к образованию хаббловского потока
Рассмотрены разные подходы к решению проблемы образования наблюдаемого хаббловского потока материи - проблемы, берущей начало с пионерских работ Сахарова. С помощью экстраполяции космологической стандартной модели в прошлое определены геометрические свойства и условия существования ранней Вселенной. Обсуждается новая концепция космогенезиса, основанная на геодезически полных геометриях чёрных/белых дыр с интегрируемой сингулярностью.
Содержание
1. Введение.
2. Уроки экстраполяции.
3. Условия космогенезиса.
4. Чёрные/белые дыры с интегрируемой сингулярностью.
5. Астрогенные вселенные.
6. Заключение.
7. Приложение.
Список литературы.
1. Введение
В своих работах (например, [1, 2]) А.Д. Сахаров неоднократно высказывал мысль о том, что космологические течения могут образовываться из сверхплотных сингулярных состояний вещества в результате квантовых переходов, сопровождаемых изменениями значений мировых постоянных, сигнатуры, стрелы времени и других геометрических характеристик пространства-времени и материи. То, каким образом гравитирующие системы или их части попадают в такие особые состояния и как они из них выходят, вызывает дискуссии в течение длительного времени вплоть до наших дней.Большие кривизны и плотности естественным образом возникают в отдельных областях пространства-времени в ходе коллапса компактных астрофизических объектов, приводящего к образованию чёрных дыр. Но задачу о том, как коллапс переходит в расширение, ещё предстоит решить. Концепция многолистной вселенной, предложенная в работах Сахарова, как и широко принятая сегодня парадигма многоэлементной вселенной (Multiverse) (см., например, [3]), требует существования ясного и простого физического механизма генерации множественных потоков расширяющегося вещества. Однако механизм космогенезиса - образования космологических потоков материи - пока не ясен. Для его исследования необходимо достаточно точно знать начальную структуру нашего материального потока, который мы называем ранней Вселенной.
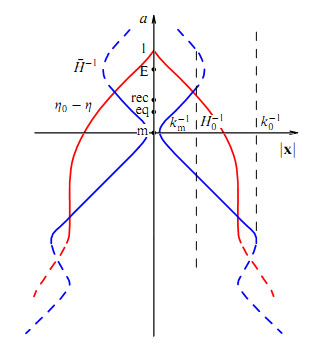
Рис. 1. По вертикальной оси отложен масштабный фактор $a$, по горизонтальной - сопутствующая координата $|\mathbf{x}|$ (мировая линия наблюдателя: $\mathbf{x} = 0$). Линия $\bar{H}^{-1}$ соответствует хаббловскому радиусу ($\bar{H}=aH$), $\eta_0-\eta$ — световой конус прошлого. Масштабы $k^{-1}_m$, $H_0^{-1}$ и $k_0^{-1}$ соответствуют нескольким долям миллиметра, величине в 4,3 Гпк и размеру фридмановского мира. Моменты времени, обозначенные как $m$, $eq$, $E$ и $rec$, отвечают окончанию инфляционной стадии БВ, началам эпох ТМ и ТЭ и рекомбинации.
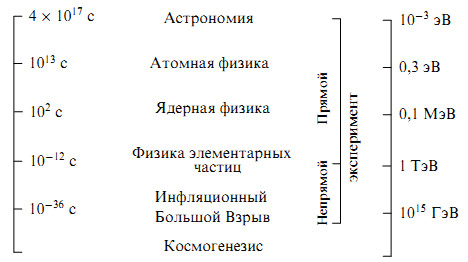
Рис. 2. Экспериментальные основания ранней Вселенной. На левой шкале - радиус кривизны Вселенной, выраженный в секундах, на правой - характерные энергии.
Задача определения геометрических свойств ранней Вселенной была успешно решена на рубеже XX XXI вв. с появлением космологической стандартной модели (КСМ), которая описывает всю совокупность экспериментальных и наблюдательных данных в диапазоне энергий $10^{-3}-10^{12}$ эВ. С созданием КСМ стало возможным посредством прямой экстраполяции в прошлое восстановить начальное состояние Вселенной, сделав единственное предположение о справедливости общей теории относительности (ОТО) при энергиях вплоть до значения энергии Великого объединения ($\sim 10^{25}$ эВ). Далее прямая экстраполяция (к ещё большим энергиям) оказалась затруднительной из-за инфляционной стадии Большого взрыва (БВ), на которой хаббловский радиус уходит за световой горизонт прошлого, где заключена большая часть информации о доинфляционной геометрии потока (рис. 1) [4]. Отклонения от квазифридмановской модели на инфляционной стадии возрастают (при экстраполяции в прошлое), поэтому структура космологического потока в начале инфляции могла сильно отличаться от фридмановской и иметь иные симметрию и топологию.
Благодаря появлению КСМ проблема генерации начального состояния расширяющегося потока (проблема космогенезиса) приобрела чёткую научную постановку в рамках исследований ОТО, поскольку энергии не превышают планковского значения. Кроме того, ввиду кратковременности прохождения гравитирующей системой сверхвысоких энергий и кривизн при рассмотрении моделей с переходом коллапса в расширение достаточно использовать лишь локальные законы сохранения, которые можно представить в общей геометрической форме тождеств Бианки. Для этого всевозможные модификации гравитации и квантово-гравитационные поправки к среднему значению тензора Эйнштейна удобно перенести в правую часть гравитационных уравнений, отнеся все эти члены к эффективному тензору энергии-импульса, включающему в себя тем самым не только материальные, но и пространственно-временные степени свободы. Такой подход позволяет сохранить понятие среднего метрического пространства-времени (независимо от значений плотности и компонент кривизны) и оставаться в классе геометрий с интегрируемыми сингулярностями [5], что делает возможным построение полных карт чёрных (белых) дыр на радиальных геодезических и позволяет понять физику гравитационной трансформации внутренней $T$-области чёрной дыры в антиколлапс рождённого вещества в белой дыре (космологическое расширение).
Далее рассмотрим уроки экстраполяции, определим начальные условия в ранней Вселенной, обсудим физическую природу многолистной вселенной и представим модели образования космологических потоков материи в рамках предложенной нами концепции космогенезиса.
2. Уроки экстраполяции
Космологическая стандартная модель опирается на широкую наблюдательную и экспериментальную базу в диапазоне энергий, охватывающем 15 порядков величины, - от текущей космологической плотности ($\sim 10^{-3}$ эВ) до исследуемых на Большом адронном коллайдере энергий электрослабого перехода ($\sim 10^{12}$ эВ), соответствующих возрасту Вселенной в несколько пикосекунд (рис. 2). Здесь нет экстраполяции - это освоенные научные знания, хорошо изученные и проверенные на Земле. Экстраполяция начинается дальше, при продвижении ещё на 13 порядков по энергии, вплоть до энергий Великого объединения.
Важнейшим результатом этих знаний являются наши представления о геометрии ранней Вселенной, под которой в ОТО понимается структура метрического тензора и тензора энергии-импульса. Эмпирически выявленная модель содержит малый параметр - амплитуду космологических неоднородностей метрики ($\sim 10^{-5}$), что позволяет привлечь для её описания теорию возмущений. В нулевом порядке мы имеем пространственно плоскую модель Фридмана, описываемую единственной функцией времени - масштабным фактором $a(t)$, зависящим от физического состава материи. В первом порядке структура тензоров более сложна - она сводится к трём неприводимым формам [6]: скалярной (возмущения плотности), тензорной (гравитационные волны) и векторной (например, магнитные поля) - каждая из которых представлена своим спектром мощности: $S(k)$, $T(k)$ и $V(k)$, где $k$ - волновое число (обратный масштаб возмущения). При случайной пространственной фазе возмущений второй и последующий порядки не содержат новых свободных функций.
Мы заключаем, что исходный космологический поток материи является полностью детерминированным и имеет ламинарный квазихаббловский характер течения (слабонеоднородная, или квазифридмановская, вселенная). Задав начальные условия и состав вещества, мы получаем в ходе развития всю палитру физических процессов и явлений современного мира. Из четырёх вышеназванных функций нам известны первые две в областях определений, доступных наблюдательной космологии. При успешной реализации действующего эксперимента Planck будет выявлен спектр космологических гравитационных волн. Детектирование векторной моды пока лежит за пределами экспериментальных возможностей.
Объяснение исходных свойств космологического потока является основной задачей космогенезиса. Физическая постановка вытекает из уроков экстраполяции [4], семь из которых мы рассмотрим ниже.
1. Вселенная - большая. Этот факт может быть объяснён наличием кратковременной инфляционной стадии БВ, предшествовавшей радиационно-доминированному периоду расширения.
Современный хаббловский радиус (радиус 4-кривизны) составляет $H_0^{-1} \simeq 4,3$ Гпк, что в планковских единицах соответствует временному запасу в 60 порядков величины. За этот период масштабный фактор, согласно КСМ, мог измениться лишь на 30 порядков, что следует из уравнений Фридмана, описывающих главный порядок теории возмущений:
$$H\equiv\frac{\dot{a}}{a}=H_0\sqrt{\frac{10^{-4}}{a^4}+\frac{0,3}{a^3}+0,7}~\rightarrow~\frac{H_0}{100a^2},~~~~~~~~~~~~~~~(1)$$ $$\gamma\equiv -\frac{\dot{H}}{H^2=\frac{2\times 10^{-4}+0,4a}{10^{-4}+0,3a+0,7a^2}}~\in~ (2,~0,4)$$(три члена под корнем отвечают излучению, нерелятивистской материи и тёмной энергии; масштабный фактор нормирован на единицу в современный момент времени). При экстраполяции в прошлое мы получаем "первичное" доминирование излучения и несколько долей миллиметра для начального размера Вселенной, что является очень большой величиной, на 30 порядков превышающей планковскую. Для объяснения такого размера необходима предшествующая инфляционная стадия со значением $\gamma < 1 $ и числом хаббловских эпох не менее семидесяти ($\sim 30~\ln 10$).
2. Принцип причинности, независимо свидетельствующий о существовании инфляционной стадии БВ. Согласно уравнениям (1), галактические масштабы оказываются в непричинной зоне в радиационно-доминированный период расширения (см. рис. 1). Они могли попасть в эту зону из причинно-связанной области при существовании кратковременной инфляционной стадии БВ.
3. Малость тензорной моды, также свидетельствующая об инфляционной стадии БВ, и гауссов характер возмущений плотности.
Если нулевой порядок теории возмущений описывается уравнениями Фридмана, то первый порядок - это осцилляторы (см. приложение). Моды $S$ и $T$ эволюционируют как безмассовые скалярные поля $q=(q_S,q_T)$, испытывающие внешнее гравитационное воздействие нестационарного хаббловского потока, что приводит к параметрическому усилению полей $q$ в ходе космологического расширения [4, 7, 8]. При достаточно общих предположениях о темпе расширения уравнения для элементарных осцилляторов допускают общее решение, однако амплитуды их возбуждений зависят от начальных данных. Для осцилляторов, изначально находившихся в основном (невозбуждённом) состоянии, спектры мощности генерируемых возмущений имеют вид
$$ T(k)\simeq\frac{H^2}{M_P^2}<10^{13} GeV,~~\frac{T}{S}\simeq 4\gamma < 1,1, ~~~~~~~~~~~~~~~(2) $$где $ \langle q^2_{S,T}\rangle =\int(S,T)gk/k,$ $ \langle … \rangle$ означает усреднение по состоянию, $M_P \equiv G^{-1/2} \equiv 10^{19}$ ГэВ - планковская масса. Как мы видим, в теории тензорная мода выступает на равных со скалярной, а их отношение зависит от величины у в эпоху параметрической генерации. Неравенства (2) отражают текущие наблюдательные ограничения на космологические гравитационные волны. Из второго неравенства следует, что величина $\gamma$ в ранней Вселенной была меньше единицы, что косвенно свидетельствует об инфляционном характере раннего хаббловского потока. Строгое доказательство первичной инфляции станет возможным в случае прямого обнаружения тензорной моды по исследованиям реликтового излучения и подтверждения предсказываемого теорией соотношения между показателем наклона $T$-спектра и отношением амплитуд мод возмущений ($n_T\equiv d \ln k \simeq -2\gamma\simeq -0,5T/S$).
Подчеркнём, что данный вывод опирается на гипотезу об идеальности раннего хаббловского потока, что выразилось в вакуумном начальном условии для полей $q$. Это предположение аргументировано наблюдаемым гауссовым случайным пространственным распределением крупномасштабных возмущений плотности (свойство квантовых флуктуации, линейно переданное полю неоднородностей) и выделенной временной фазой звуковых колебаний, соответствующей растущей адиабатической ветви эволюции (свойство параметрического эффекта усиления).
4. Наличие тёмной материи. Нелинейные гало, внутри которых "живут" галактики, состоят из нерелятивистских частиц тёмной материи (ТМ), не взаимодействующих с барионами и излучением. Природа частиц ТМ пока неизвестна, однако существуют наблюдательные аргументы в пользу того, что происхождение ТМ связано с барионной асимметрией Вселенной. Вот два из них: космологические плотности массы ТМ и барионов близки друг к другу (их отношение равно 5) и совпадают масштабы их пространственных крупномасштабных распределений (космологический горизонт на момент равенства плотностей релятивистского и нерелятивистского компонентов материи идентичен звуковому горизонту на момент рекомбинации водорода). Если принять во внимание, что отношение плотностей двух нерелятивистских сред неизменно во времени, то мы приходим к выводу, что причины появления ТМ и барионной асимметрии связаны между собой. Можно предположить, что как частицы ТМ, так и избыточные барионы возникли в ходе неравновесных процессов преобразований частиц в высокотемпературной радиационной плазме хаббловского потока. Тогда их происхождение не связано с доинфляционной историей БВ.
5. Свидетельство в пользу существования тёмной энергии. Материя, формирующая структуру Вселенной, измеряется по градиентам гравитационного потенциала на основе динамических наблюдений галактик и газа и с помощью гравитационного линзирования. Её количество не превышает 30 % критической плотности. Остальные 70 % находятся в однородно распределённой подсистеме, не взаимодействующей со светом и барионами. Это так называемая тёмная энергия (ТЭ), имеющая отрицательное эффективное давление, сопоставимое по модулю с её плотностью энергии. По-видимому, здесь мы имеем дело с "законсервированным" на стадии доминирования излучения и частиц реликтовым сверхслабым полем, пришедшим в движение (в режиме медленного скатывания) под действием собственной гравитации 3,5 млрд лет назад. Если это так, то мы являемся свидетелями релаксации массивного поля, что позволяет по-иному взглянуть на историю хаббловского потока.
6. История эволюции Вселенной. Мы видим, что в эволюции были периоды ускоренного ($\gamma < 1$) и замедленного ($\gamma > 1$) расширения. К первому случаю относятся инфляционные стадии БВ и ТЭ, ко второму - радиационно- и материально-доминированные стадии. Мы знаем, что малые возмущения затухают при $\gamma < 1$ и возрастают при $\gamma > 1$. Отсюда следует, что в истории Вселенной были как этапы построения (восстановления) хаббловского потока, так и этапы его разрушения (тогда мы говорим об образовании структуры). В этом проявляется двойственный характер дальнодействующей гравитации, способной создавать строго упорядоченные системы из достаточно общих начальных распределений и состояний материи. Это антиколлапс, или инфляция (построение идеального хаббловского потока), и противоположный ему процесс коллапса (образование гравитационно связанных гало и чёрных дыр). Таким образом, мы можем взглянуть на динамическую историю потока как на насчитывающую 14 млрд лет историю релаксации массивных полей к состоянию минимальной энергии. Здесь мы вплотную подошли к последнему (седьмому) уроку экстраполяции КСМ к доинфляционной вселенной. Как создать необходимые условия для возникновения расширяющегося материального потока, подхваченного инфляцией и превратившегося в наблюдаемое хаббловское течение?
3. Условия космогенезиса
Итак, решение проблемы космогенезиса - это ответы на три вопроса.
- Как возникают большие плотности?
- Откуда берётся расширение?
- Каково происхождение космологической симметрии?
Инфляция не даёт ответов на эти вопросы. В различных её вариантах (например, [9, 10]) вводятся новые физические поля, которые с самого начала находятся в сверхплотном состоянии. Рождение Вселенной из "ничего" [11] опять приводит к представлению о "ложном" вакууме с высокой плотностью, а в развиваемых в течение более 40 лет моделях с отскоками, в которых вопрос о начальном состоянии теряет смысл (благодаря модификациям уравнения состояния), фридмановская симметрия вводится аксиоматично.
Фундаментальный естественнонаучный принцип, гласящий, что в любом решении, которое описывает природу, все измеримые величины должны оставаться конечными, позволяет продвинуться в решении проблемы космогенезиса. Действительно (см. [5]), если рассмотреть реалистичные модели чёрных/белых дыр со сглаженными метрическими особенностями, то удаётся ограничить приливные силы (несмотря на расходимость некоторых компонент кривизны) и восстановить геодезически полное метрическое пространство-время на основе динамических решений, вытекающих из законов сохранения энергии-импульса. Вблизи особенности, возникающей вокруг коллапсировавшего объекта, находится эффективная материя, которую мы моделируем в широком классе уравнений состояния. Радиальные геодезические теперь не заканчиваются на сингулярной гиперповерхности, а продолжаются в $T$-область белой дыры. Отсюда мы приходим к выводу, что $T$-область чёрной/белой дыры, образовавшаяся в результате коллапса астрофизической компактной системы, может давать начало новой (дочерней или астрогенной) вселенной, находящейся в абсолютном будущем по отношению к материнской чёрной дыре. Тогда ответы на поставленные вопросы почти очевидны:
- высокие кривизны и плотности на начальных стадиях космологической эволюции возникают вследствие сверхсильных быстропеременных гравитационных полей, существующих внутри чёрной/белой дыры и рождающих собственное вещество дочерней вселенной;
- первичный толчок космологическому потоку эффективной материи даёт расширяющаяся $T$-область белой дыры, образовавшаяся в результате коллапса компактного объекта в материнской вселенной. Тем самым феномен БВ имеет чисто гравитационную природу и представляет собой проявление гравитационной (приливной) неустойчивости;
- симметрия внутренней области чёрной/белой дыры вне тела коллапсировавшей системы является однородной космологией, в которой материальный поток в белой дыре может изотропизоваться посредством известных механизмов инфляции и тем самым белая дыра превратится во фридмановский мир.
4. Чёрные/белые дыры с интегрируемой сингулярностью
Применение вышеупомянутого принципа к сферически симметричным метрикам общего типа означает ограниченность действительных функций $N$ и $\Phi$ в $\mathbb{R}^2\in (r,t):$
$$ ds^2 = N^2(1+2\Phi)dt^2 - \frac{dr^2}{1+2\Phi} - r^2d\Omega,~~~~~~~~~~~~~~~(3) $$где $r$ и $t$ - радиальная и временная эйлеровы координаты в $R$-областях пространства-времени ($\Phi > - 1/2$) и соответственно временная и пространственная координаты того же решения в $T$-областях ($\Phi < -1/2$ (см. [12])), $d\Omega$ — квадрат интервала на поверхности 2-сферы. Из уравнений ОТО следует
$$ \Phi=-\frac{Gm}{r},~~~~~~~~~~~~~~~(4) $$где всюду непрерывная функция массы
$$ m=m(r,t)=4\pi\int_0 T_t^t r^2 dr ~~~~~~~~~~~~~~~(5) $$Мы полагаем, что эта материя может индуцироваться интенсивным быстропеременным гравитационным полем (вследствие квантово-гравитационных процессов поляризации вакуума и рождения вещества), существующим вне коллапсировавшего объекта в $T$-области чёрной/белой дыры. Тогда симметрия полного решения сохраняет глобальный (-вектор Киллинга, содержащийся в оригинальной шварцшильдовской метрике в вакууме, и все рассматриваемые физические переменные являются функциями только $r$ (считаем, что $r>0$ в материнской чёрной дыре и $r>0$ после продолжения метрики в $T$-области через линию $r=0$).
обращается в нуль на линии инверсии $r = 0$ ввиду требования конечности потенциала $\Phi$; $T_t^t$ - это $tt-$компонента тензора энергии-импульса. Интегрируемость функции $T_t^t r^2$ в нуле (при конечной массе чёрной дыры) приводит нас к понятию интегрируемой сингулярности $r=0$, окружённой эффективной материей (см. сноску слева). При отсутствии пространственных потоков в $T$-области тензор энергии-импульса имеет вид $T_\mu^\nu = diag(-p,\varepsilon,-p_\bot,-p_\bot)$. В разделе 5 мы приводим примеры моделей, в которых плотность энергии генерируется вариациями поперечного давления $ p_\bot $, изменяющегося триггерным образом в определённые моменты времени $r$. В этих моделях приливные силы для радиальных геодезических всюду конечны и мировые линии пробных частиц продолжаются из $T$-области чёрной дыры в белую (подробнее см. [5]). Таким образом, приливное гравитационное взаимодействие в окрестности интегрируемой сингулярности имеет вид временной осцилляции, соединяющей внутренние области чёрной и белой дыр. Этот эффект мы называем инверсией коллапса.
5. Астрогенные вселенные
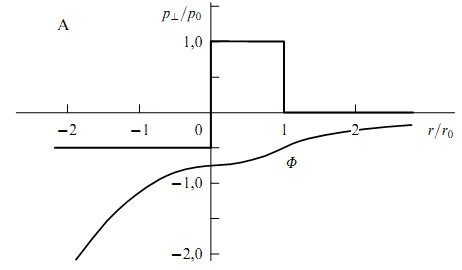
Рис. 3. Асимметричный профиль поперечного давления (жирная ломаная линия), приводящий к обращению коллапса в космологическое расширение, которое асимптотически стремится к де-ситтеровскому решению. Кривой показана эволюция гравитационного потенциала для модели, в которой вещество заполняет всю $T$-область чёрной дыры ($r_0=2GM$). Кроме того, в качестве примера принятого $p_1/p_0=$0,5.
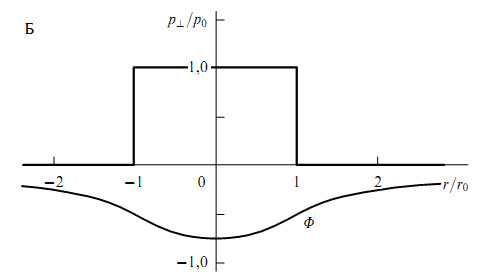
Рис. 4. Симметричный профиль поперечного давления (жирная ломаная линия), приводящий к превращению чёрной дыры в белую с той же массой. Кривой показана эволюция гравитационного потенциала в модели, где вещество заполняет $T$-области чёрной и белой дыр полностью (($r_0=2GM$).
Материю в $T$-областях сферически симметричных вакуумных геометрий можно генерировать с помощью временных вариаций функции $ p_\bot (r)$, например скачков первого рода, поскольку уравнения движения не содержат её производных (энергия черпается из гравитационного поля и метрика автоматически перестраивается в соответствии с ОТО). Продольное давление удобно выбрать для простоты "вакуумноподобным" ($p= \varepsilon $), тогда $N = 1$ всюду в $ \mathbb{R}^2 $ и система отсчёта (3) сопутствует материи, а плотность энергии определяется из тождества Бианки
$$ \frac{d(\varepsilon r)^2}{rdr}=-2p_\bot .~~~~~~~~~~~~~~~(6) $$Рассмотрим два простых варианта поведения функции $2p_\bot $ (рис. 3, 4):
А) асимметричная ступенька, $p_\bot^{(A)}=p_0\theta (r(r_0-r))-p_1\theta(-r);$
B) симметричная ступенька, $p_\bot^{(B)}=p_0\theta (r^2_0-r^2)$, где $r_0\leq 2GM$ и $p_1$ — действительные положительные постоянные, $M\equiv 8\pi r^3_0p_0/3$ - масса чёрной дыры. Интегрирование уравнения (6) с начальным условием $\varepsilon(r\geq r_0)=0$ даёт следующие непрерывные функции $ \varepsilon (r)$:
$$ \varepsilon^{(A)}=-p_\bot^{(A)}+p_0\frac{r_0^2}{r^2}\theta(r_0-r),~~\varepsilon^{(B)}=p_\bot^{(B)}\left(\frac{r_0^2}{r^2}-1\right). ~~~~~~~~~~~~~~~(7) $$Таким образом, $A$ - это модель астрогенной вселенной ($\varepsilon^{(A)} \rightarrow p_1$ при $r\rightarrow -\inf$) а $B$ - пример осциллирующей (вечной) чёрной/белой дыры. Потенциал $\Phi(r)$ принадлежит классу функций $C^1$ (см. (4), (5) и рис. 3, 4).
Рассмотрим предельные случаи варианта B. При $r_0 \rightarrow 0$ имеем максимально продолженную в пустоту вечную чёрную/белую дыру с $\delta$-образным источником, локализованным в области $r=0$ [5]:
$$ \varepsilon=2p_\bot =M\frac{\delta(r)}{2\pi r^2} ~~~~~~~~~~~~~~~(8) $$При предельном расширении $r_0=2GM$ получаем стационарную дыру с осциллирующим потоком материи в $T$-области, где $r=-2GM\sin(H\tau)$, $H^{-1}\equiv 2\sqrt{2}GM$, $\tau$ -частота осцилляции и собственное время потока,
$$ \varepsilon=\frac{3H^2}{8\pi G}\cot(H\tau), ~~~~~~~~~~~~~~~(9)$$ $$ ds^2=d\tau^2-\frac 12 \left(\cos^2(H\tau)dt^2+\frac{\sin^2(H\tau)}{H^2}d\Omega\right) $$Здесь мы имеем дело с пространственно однородным, анизотропным и пульсирующим течением материи, полная диаграмма Пенроуза которого представлена на рис. 5. Фазовые переходы в материи на стадии её объёмного расширения способны привести к инфляции и изотропизовать поток, установив тем самым фридмановскую симметрию в сколь угодно большом объёме.
Простейший пример подобного сценария иллюстрируется случаем А. Действительно, при $ \tau\geq 0 $ из (7) имеем решение, асимптотически приближающееся к де-ситтеровскому (рис. 6):
$$ r=-\frac{\sinh(H_1\tau)}{\sqrt{2}H_1},~~\varepsilon=\frac{3H_1^2}{8\pi G}\coth^2(H_1\tau),~~~~~~~~~~~~~~~(10)$$ $$ ds^2=d\tau^2-\frac 12 \left(\cos^2(H\tau)dt^2+\frac{\sinh^2(H_1\tau)}{H_1^2}d\Omega\right) $$где постоянная $H_1=(8\pi Gp_1/3)^{1/2}$ принимает любые значения, вне зависимости от величины внешней массы материнской чёрной дыры. Данный элементарный пример астрогенной вселенной легко обобщается для более сложных моделей с привлечением массивных скалярных полей, излучения и других элементов современной "кухни" КСМ.
6. Заключение
Экстраполяция КСМ в прошлое свидетельствует о расширяющемся начальном хаббловском потоке материи со сверхбольшими кривизнами и плотностями. В моделях чёрных/белых дыр с интегрируемой сингулярностью космологические течения могут возникать в расширяющихся $T$-областях этих геометрий (белых дырах), лежащих в абсолютном будущем по отношению к материнской чёрной дыре. В рамках предложенной концепции мы приходим к понятию астрогенной космологии - космологии, получающейся инверсией коллапса какой-либо астрофизической компактной системы в расширяющийся поток эффективной материи вне родительского тела самого коллапсировавшего объекта. Образно говоря, чёрные дыры в этих моделях играют роль спичек, зажигающих иные миры.
Возможно, многолистные вселенные со сложной топологией, которые предвидел и обсуждал Сахаров, обязаны своим существованием коллапсировавшим системам, завершившим свою эволюцию в материнской Вселенной. Научные теории имеют предсказательную силу и должны проверяться экспериментально и с помощью наблюдений. Эти вопросы вдохновляют нас на новые исследования загадок и проблем космогенезиса.
7. Приложение
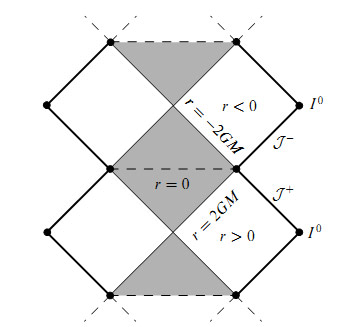
Рис. 5. Диаграмма Пенроуза пульсирующего потока с симметричной функцией $p_\bot(r)$ (см. рис. 4). Затемнённая область занята материей. $\mathcal{J^+}$— световая бесконечность будущего для наблюдателей в области $r>0,~\mathcal{J}^-$ — световая бесконечность прошлого для наблюдателей в области $r<0,~I^0$ - пространственные бесконечности $R$-областей.

Рис. 6. Диаграмма Пенроуза астрогенной вселенной с асимметричной функцией $p_\bot(r)$ (см. рис. 3).
Напомним [4], что $q_S=\delta a/a+H\upsilon$ и $\upsilon$ - это возмущения сопутствующего масштабного фактора и потенциала скорости материи соответственно, $q_T=(q_\lambda)$ - амплитуды гравитационных волн с поляризацией $\lambda=\oplus,\otimes$. Конформные поля $\tilde{q}=\tilde{\alpha}q/\sqrt{8\pi G}$ ведут себя как классические гармонические осцилляторы в пространстве Минковского с переменными частотами:
$$ \tilde{q}''+(\omega^2-U)\tilde{q}=0,~~~~~~~~~~~~~~~(11) $$
где штрих означает производную по минковскому времени $\eta-\int dt/a,$
$$U\equiv\frac{\tilde{\alpha}''}{\tilde{\alpha}},~~U_T=(2-\gamma)a^2H^2,~~\tilde{\alpha}_S=\frac{a\sqrt{2\gamma}}{\beta},~~\tilde{\alpha}_T=a,$$
$\omega=\beta k,~\beta_S$ - скорость звука в единицах скорости света, $\beta_T=1$. В случае двух и более сред в правую часть уравнений для $S$-осцилляторов следует добавить член, описывающий воздействие изометрических возмущений. Зависимость эффективной частоты ($\omega^2-U$) от времени приводит к параметрическому возбуждению элементарных осцилляторов в ходе эволюции Вселенной. Предполагая начальное вакуумное состояние полей в волновой зоне ($\omega^2>|U|$), переходящей со временем в параметрическую ($|U|>\omega^2$), получаем требуемое решение (11) (см. подробнее [4]):
где $\mathcal{C}$ — постоянная сшивки в области $|U|\simeq\omega$, функция $\mathbf{c}=-k\mathcal{C}^2\int\tilde{\alpha}^{-2}d\eta\rightarrow const$ сходится на верхнем пределе при $\gamma<3$. "Замороженные" поля $q_k$ соответствуют возрастающей ветви общего решения, их фаза случайна, а модуль определяет спектральные амплитуды $S=|q_{kS}|^2$ и $T=|q_{k\oplus}|^2+|q_{k\otimes}|^2$. При $\beta=1$ и $\gamma\simeq const$ уравнения (11) для всех мод идентичны и $T/S=2\tilde{\alpha}^2_S/\tilde{\alpha}^2_T=4\gamma$ при $\gamma<1$ получаем $T$-спектр (2) с точностью до множителя порядка единицы.
В.Н. Лукаш, Е.В. Михеева, В.Н. Строков
Список литературы
- Сахаров А Д ЖЭТФ 83 1233 (1982) [Sakharov A D Sov. Phys. JETP 56 705 (1982)]
- Сахаров А Д ЖЭТФ 87 375 (1984) [Sakharov A D Sov. Phys. JETP 60 214(1984)]
- Carr B (Ed.) Universe or Multiversel (Cambridge: Cambridge Univ. Press, 2007)
- Лукаш В Н, Михеева Е В Физическая космология (М.: Физмат-лит,2010)
- Lukash VN, Strokov VN, arXiv: 1109.2796
- Лифшиц Е М ЖЭТФ 16 587 (1946)
- Лукаш В Н Письма в ЖЭТФ 31 631 (1980) [Lukash V N JETP Lett. 31 596 (1980)]
- Лукаш В Н ЖЭТФ 79 1601 (1980) [Lukash V N Sov. Phys. JETP52 807 (1980)]
- Guth A H Phys. Rev. D 23 341 (1981)
- Linde A D Phys. Lett. В108 389 (1982)
- Долгов А Д, Зельдович Я Б, Сажин М В Космология ранней Вселенной (М.: Изд-во МГУ, 1988) [Dolgov A D, Sazhin M V, Zeldovich Ya В Basics of Modern Cosmology (Gif-sur-Yvette: Editions Frontieres, 1990)]
- Новиков И Д Астрон. журн. 38 564 (1961) [Novikov I D Astron. Zh. 5 423(1961)]
Оригинал статьи и pdf версия на сайте журнала УФН
Нет комментариев.
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.