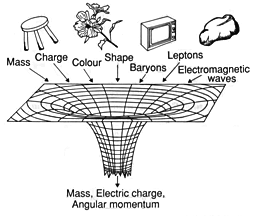
Чёрные дыры: дружественный шарж
В наше время трудно найти человека, который не слышал бы о чёрных дырах. Вместе с тем, пожалуй, не менее трудно отыскать того, кто смог бы объяснить, что это такое. Впрочем, для специалистов чёрные дыры уже перестали быть фантастикой – астрономические наблюдения давно доказали существование как «малых» чёрных дыр (с массой порядка солнечной), которые образовались в результате гравитационного сжатия звёзд, так и сверхмассивных (до $10^9$ масс Солнца), которые породил коллапс целых звёздных скоплений в центрах многих галактик, включая нашу. В настоящее время микроскопические чёрные дыры ищут в потоках космических лучей сверхвысоких энергий (международная лаборатория Pierre Auger, Аргентина) и даже предполагают «наладить их производство» на Большом адронном коллайдере (LHC). Однако подлинная роль чёрных дыр, их «предназначение» для Вселенной, находится далеко за рамками астрономии и физики элементарных частиц. При их изучении исследователи глубоко продвинулись в научном понимании прежде сугубо философских вопросов – что есть пространство и время, существуют ли границы познания Природы, какова связь между материей и информацией. Попытаемся осветить всё наиболее важное по этой теме.
О сингулярности, информации, энтропии, космологии и многомерной Единой теории взаимодействий в свете современной теории чёрных дыр.
1. Тёмные звёзды Митчелла – Лапласа
Термин «чёрная дыра» был предложен Дж. Уилером в 1967 году, однако первые предсказания существования тел столь массивных, что даже свет не может их покинуть, датируются XVIII веком и принадлежат Дж. Митчеллу и П. Лапласу. Их расчёты основывались на теории тяготения Ньютона и корпускулярной природе света. В современном варианте эта задача выглядит так: каковы должны быть радиус Rs и масса M звезды, чтобы её вторая космическая скорость (минимальная скорость, которую необходимо сообщить телу на поверхности звезды, чтобы оно вышло из сферы её гравитационного действия) равнялась скорости света c? Применяя закон сохранения энергии, получаем величину
Rs = 2GM / c 2, |
(1) |
которая известна как радиус Шварцшильда, или радиус сферической чёрной дыры (G – гравитационная постоянная). Несмотря на то, что теория Ньютона заведомо неприменима к реальным чёрным дырам, формула (1) сама по себе верна, что и подтвердил немецкий астроном К. Шварцшильд в рамках общей теории относительности (ОТО) Эйнштейна, созданной в 1915 году! В этой теории формула определяет, до какого размера должно сжаться тело, чтобы получилась чёрная дыра. Если для тела радиуса R и массы M выполняется неравенство
|
Вблизи коллапсирующей звезды траектория светового луча искривляется её гравитационным полем. Чем меньше радиус звезды, тем это искривление сильнее, так что луч может сделать несколько оборотов, прежде чем уйдёт в пространство. Когда её радиус станет меньше радиуса Шварцшильда (показан пунктирной линией), свет будет возвращаться на поверхность звезды. Возникнет чёрная дыра. |
 |
2. Чёрные дыры от Эйнштейна до Хокинга
По-настоящему последовательная и непротиворечивая теория чёрных дыр, или коллапсаров, невозможна без учёта искривляемости пространства-времени. Поэтому неудивительно, что они естественным образом появляются как частные решения уравнений ОТО. Согласно им, чёрная дыра – это объект, искривляющий пространство-время в своей окрестности настолько, что никакой сигнал не может быть передан с её поверхности или изнутри даже по световому лучу. Иными словами, поверхность чёрной дыры служит границей пространства-времени, доступного нашим наблюдениям. Вплоть до начала
Энтропия чёрных дыр. В 1972 году Я. Бекенштейн высказал гипотезу, что чёрная дыра обладает энтропией, пропорциональной площади её поверхности A (для сферической дыры A = 4πRs2 ):
SЧД = C ∙ A / 4, |
(2) |
где C = kc3 / Gћ – комбинация фундаментальных констант (k – постоянная Больцмана и ћ – постоянная Планка). Кстати, теоретики предпочитают работать в планковской системе единиц, в этом случае
ΔStot. ≡ (Stot.)конечн.– (Stot.)начальн. ≥ 0, |
(3) |
то есть суммарная энтропия системы не может уменьшаться. Последняя формула полезна также тем, что из неё можно вывести ограничение на энтропию обычной материи. Рассмотрим так называемый процесс Сасскинда: имеется сферически-симметричное тело «субкритической» массы, то есть такой, которая ещё удовлетворяет условию гравитационной устойчивости, однако достаточно добавить немного энергии-массы ΔE, чтобы тело сколлапсировало в чёрную дыру. Тело окружено сферической оболочкой (чья суммарная энергия как раз равна ΔE), которая падает на тело. Энтропия системы до падения оболочки:
(Stot.)начальн. = Sвещество+ Sоболочка , |
после:
(Stot.)конечн. = SЧД = A / 4. |
Из (3) и неотрицательности энтропии получаем знаменитое ограничение сверху на энтропию вещества:
Sвещество ≤ A / 4, |
(4) |
Формулы (2) и (3), несмотря на их простоту, породили загадку, оказавшую огромное влияние на развитие фундаментальной науки. Из стандартного курса статистической физики известно, что энтропия системы является не первичным понятием, а функцией от степеней свободы микроскопических составляющих системы – например, энтропия газа определяется как логарифм числа возможных микросостояний его молекул. Таким образом, если чёрная дыра имеет энтропию, то она должна обладать внутренней структурой! Только в последние годы наметился подлинно большой прогресс в понимании этой структуры 1, а тогда идеи Бекенштейна были вообще скептически восприняты физиками. Стивен Хокинг, по его собственному признанию, решил опровергнуть Бекенштейна его же оружием – термодинамикой.
Излучение Хокинга. Коль скоро (2) и (3) наделены физическим смыслом, первый закон термодинамики диктует, что чёрная дыра должна иметь температуру T. Но позвольте, какая может быть у неё температура?! Ведь в таком случае дыра должна излучать, что противоречит её главному свойству! Действительно, классическая чёрная дыра температуры, отличной от абсолютного нуля, иметь не может. Однако если предположить, что микросостояния чёрной дыры подчиняются законам квантовой механики, что, вообще говоря, практически очевидно, то противоречие легко устранимо. Согласно квантовой механике, а точнее, её обобщению – квантовой теории поля, может происходить спонтанное рождение частиц из вакуума. При отсутствии внешних полей пара частица-античастица, рождённая таким образом, аннигилирует обратно в вакуумное состояние. Однако если поблизости есть чёрная дыра, её поле притянет ближайшую частицу. Тогда, по закону сохранения энергии-импульса, другая частица уйдёт на бoльшее расстояние от чёрной дыры, унося с собой «приданое» – часть энергии-массы коллапсара (иногда говорят, что «чёрная дыра потратила часть энергии на рождение пары», что не совсем корректно, ибо выживает не вся пара, а только одна частица).
Как бы то ни было, в результате удалённый наблюдатель обнаружит поток всевозможных частиц, излучаемых чёрной дырой, которая будет расходовать свою массу на рождение пар, пока полностью не испарится, превратившись в облако излучения 2. Температура чёрной дыры обратно пропорциональна её массе, таким образом, более массивные испаряются медленнее, ибо время их жизни пропорционально кубу массы (в четырёхмерном пространстве-времени). Например, время жизни чёрной дыры с массой M порядка солнечной превосходит возраст Вселенной, тогда как микродыра с M = 1 тераэлектронвольт (1012 эВ, примерно
 |
||
|
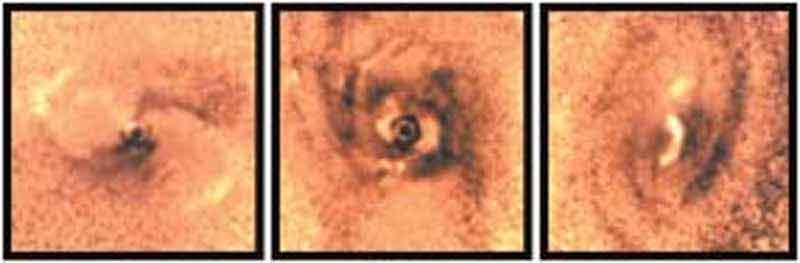
Markarian 573 |
NGC 5674 |
UGC 6100 |
 |
||
|
NGC 3982 |
NGC 5273 |
NGC 5929 |
|
Чёрные дыры, заснятые космическим телескопом «Хаббл» в центрах шести галактик. Они втягивают окружающую материю, которая образует спиральные рукава и падает на чёрную дыру, навсегда скрываясь за горизонтом событий. |
||
3. Чёрные дыры и сингулярности
В научно-фантастической литературе и фильмах чёрная дыра обычно представляется этаким космическим Гаргантюа, безжалостно пожирающим пролетающие корабли с отважными блондинками и даже целые планеты. Увы, если бы фантасты знали о современной физике чуть больше, они бы не были столь несправедливы к чёрным дырам. Дело в том, что коллапсары фактически защищают Вселенную от гораздо более грозных монстров…
Сингулярностью называется точка пространства, в которой его кривизна неограниченно стремится к бесконечности, – пространство-время как бы рвётся в этой точке. Современная теория говорит о существовании сингулярностей как о неизбежном факте 3 – с математической точки зрения, решения уравнений, описывающие сингулярности, также равноправны, как и все прочие решения, описывающие более привычные объекты Вселенной, которые мы наблюдаем.
Есть тут, однако, очень серьёзная проблема. Дело в том, что для описания физических явлений необходимо не только иметь соответствующие уравнения, но нужно также задать граничные и начальные условия. Так вот, в сингулярных точках эти самые условия задать нельзя в принципе, что делает предсказательное описание последующей динамики невозможным. А теперь представим, что на раннем этапе существования Вселенной (когда она была достаточно малой и плотной) образуется множество сингулярностей. Тогда в областях, которые находятся внутри световых конусов этих сингулярностей (иными словами, причинно-зависимых от них) никакое детерминистское описание невозможно. Мы имеем абсолютный и бесструктурный хаос, без намёка на какую-либо причинность. Далее, эти области хаоса расширяются со временем по мере эволюции Вселенной. В результате к настоящему времени подавляющая часть Вселенной была бы совершенно стохастичной (случайной) и ни о каких «законах природы» не могло бы быть и речи. Не говоря уже о блондинках, планетах и прочих неоднородностях вроде нас с вами.
К счастью, ситуацию спасают наши ненасытные обжоры. Математическая структура уравнений фундаментальной теории и их решений указывает на то, что в реальных ситуациях пространственные сингулярности должны появляться не сами по себе, а исключительно внутри чёрных дыр. Как тут не вспомнить мифологических титанов, пытавшихся воцарить Хаос на Земле, но низвергнутых Зевсом и Ко в Тартар и благополучно заключенных там навеки…
Таким образом, чёрные дыры отделяют сингулярности от остальной Вселенной и не позволяют им влиять на её причинно-следственные связи. Этот принцип запрета существования «голых» (англ. naked) сингулярностей, то есть не окружённых горизонтом событий, предложенный Р. Пенроузом в 1969 году, получил название гипотезы космической цензуры. Как это часто бывает с фундаментальными принципами, полностью он не доказан, но принципиальных нарушений пока замечено не было – Космический цензор на пенсию пока не собирается.
Информационный парадокс черных дыр слегка распутан
|
Квантовая информация обладает поразительным свойством: она может физически присутствовать в нашем мире, но быть совершенно недоступной для «считывания». Это свойство отчасти разрешает информационный парадокс черных дыр.
Многие «парадоксы», с которыми иногда приходится сталкиваться в жизни, являются на самом деле не настоящими логическими противоречиями, а лишь результатом неправильного использования терминов и понятий там, где их применять нельзя. Преподаватели знают, что очень полезно ставить перед студентом такого рода «парадоксы» для углубления понимания дисциплины.
И вот сейчас на удочку, похоже, попались сами ученые. Как утверждается в статье J. A. Smolin and J. Oppenheim, Physical Review Letters, 96, 081302 (28 February), доступной также как hep-th/0507287, знаменитый клубок парадоксов, связанных с (не)исчезновением информации в черной дыре, возникает, по крайней мере, отчасти из-за неправильного использования понятия информации в квантовой теории.
Напомним вкратце суть проблемы.
Квантовая механика прекрасно описывает мир микрочастиц, в котором гравитация столь слаба, что ею обычно пренебрегают. Общая теория относительности, наоборот, описывает гравитационные явления в астрономических масштабах, там, где квантовые эффекты не важны. Обе эти теории безупречно выполняются в своих областях применимости и не мешают друг другу.
По-настоящему столкнулись эти две теории в 1975 году, когда Стивен Хокинг открыл, что черные дыры обязаны «испаряться»: фотон за фотоном излучать свою энергию в окружающее пространство, сами при этом постепенно уменьшаясь. Тут-то и оказалось, что свойства этого процесса, вычисленные по теории относительности, противоречат основным постулатам квантовой теории. Получается, либо общая теория относительности, либо квантовая механика в этом конкретном процессе перестанут работать, но кто именно — пока неизвестно (впрочем, сам Стивен Хокинг уже пришел к определенной точке зрения).
Физики эту дилемму обычно формулируют в виде информационного парадокса. При теоретическом описании любого тела физики оперируют характеризующей его информацией: количеством молекул, их движением, их взаимным расположением и т.п. И при падении тела в черную дыру эта информация поглощается вместе с телом.
Если приближение, использованное Хокингом в вычислениях, справедливо, то черная дыра будет служить универсальным уничтожителем информации. Не важно, что и в каком состоянии в нее упадет: в результате испарения будет всегда один и тот же беспорядочный набор фотонов. Первоначальная информация, заключенная в теле, исчезает из нашего мира напрочь, и это противоречит одному из главных постулатов квантовой механики.
Если же вычисления Хокинга неточны, а квантовая механика, наоборот, применима и в этом случае, то вылетающие фотоны будут содержать в себе информацию об упавшем в черную дыру теле, и ее, теоретически, можно восстановить, полностью или частично (хоть с практической точки зрения это нереально). Остается, однако, непонятным, почему в этом случае не срабатывает теория относительности.
Были, конечно, и попытки примирить эти две теории. Например, можно предположить, что информация не исчезает, а лишь накапливается внутри черной дыры, оставаясь недоступной внешнему миру. И лишь в последний момент, когда испарятся последние остатки микроскопической черной дыры (для которой расчеты Хокинга заведомо неприменимы), вся информация и выйдет наружу. Впрочем, скептики сразу же возразили: микроскопическая черная дыра слишком мала, чтобы удержать столько информации, а значит, это предложение не проходит.
И вот тут-то интуиция и подвела физиков. На самом деле, как подчеркивается в статье, из того факта, что информация пока что не вышла из черной дыры, вовсе не следует, что она все еще внутри!
Авторы напоминают, что свойства квантовой информации отличаются от свойств обычной, классической информации. Квантовая информация не обязана быть локализована где-то в пространстве и, как недавно было обнаружено, ее часто нельзя разделить на части. Иными словами, если взять «квантовую книгу» и разделить ее на две части, то может оказаться, что ни одна из половинок не даст нам вообще никакой информации.
В случае черных дыр возможна даже такая ситуация: материальные носители, фотоны, в процессе утечки информации наружу нам доступны, мы знаем, что они как-то кодируют в себе эту информацию, но расшифровать ее нельзя даже в принципе. Грубо говоря, невозможно определить, что именно у фотонов надо измерить, чтобы извлечь эту информацию.
Получается, что весь огромный объем информации вовсе не обязан прятаться внутри черной дыры; он может присутствовать во внешнем мире, но быть столь «намертво» зашифрованным, что окажется недоступным ни для какого наблюдения. Для того, чтоб получить доступ к этой «летописи», надо дождаться самых последних битов этого потока информации (а их микроскопическая черная дыра удержать вполне может), которые и послужат ключом к полной расшифровке.
Авторы подчеркивают, что они вовсе не предъявляют полное решение информационного парадокса черных дыр: оно будет получено лишь после создания более или менее цельной теории квантовой гравитации. Однако они доказывают, что, по крайней мере, некоторые грани этой проблемы есть лишь следствие неправильных аналогий и к исходному вопросу имеют мало отношения.
4. «Информационоёмкость» материи и теория великого объединения
Локальная квантовая теория прекрасно зарекомендовала себя при описании всех известных элементарных взаимодействий, кроме гравитационного. Стало быть, фундаментальная квантовая теория с учётом ОТО также принадлежит к этому типу? Если принять эту гипотезу, нетрудно показать, что максимальное количество информации S, которое можно запасти в куске вещества объема V, равно V, измеренному в планковских единицах объема
Sвещество ~ V. |
(5) |
Однако эта формула вступает в противоречие с (4), так как в планковских единицах A намного меньше V для известных физических систем (соотношение A / V составляет порядка
Это, в свою очередь, может означать, что подлинно фундаментальная теория материи не просто очередная модификация квантовой теории поля, сформулированной «по объёму», а некая теория, «живущая» на определённой поверхности, ограничивающей этот объём. Гипотеза получила название голографического принципа, по аналогии с оптической голограммой, которая, будучи плоской, тем не менее даёт объёмное изображение. Принцип сразу же вызвал большой интерес, ибо теория «на поверхности» – это нечто принципиально новое, вдобавок сулящее упрощение математического описания: ввиду понижения пространственной размерности на единицу, поверхности имеют меньшее число геометрических степеней свободы. В полной мере голографическая гипотеза пока не доказана, но уже существуют два общепризнанных подтверждения – ковариантное ограничение на энтропию вещества
Первое даёт рецепт вычисления статистической энтропии (4) для общего случая материального тела, как определённой величины, вычисляемой на светоподобных мировых поверхностях, ортогональных поверхности тела (да простит меня неискушенный читатель за эту фразу). Общая идея состоит в следующем. Что принять за меру энтропии в искривленном пространстве-времени, то есть как её посчитать правильно? Например, в случае распределения шара по ящикам (см. «Подробности для любознательных») мерой энтропии фактически является число ящиков, в случае обычного газа – его объём, отнесенный к усредненному объёму молекулы. Но в четырехмерном пространстве-времени объём чего бы то ни было величина не абсолютная (помните лоренцево сокращение длин?). Ну а понятие «ящика», сами понимаете, несколько выходит за рамки элементарных понятий фундаментальной науки. В общем, необходимо определить меру энтропии через элементарные понятия дифференциальной геометрии, которые были бы ковариантными, то есть значения которых менялись бы в зависимости от положения наблюдателя чётко определённым образом.
Пусть N – светоподобная гиперповерхность (обобщённый световой конус) некоторой совокупности пространственных точек S. Грубо говоря, N – это множество фотографий S, сделанных через бесконечно малые промежутки времени. Возьмём два пространственных среза N, сделанных в различные моменты времени (две «фотографии»), назовём их S1 и S2. Тогда принцип ковариантного ограничения на энтропию вещества, находящегося в S, гласит, что поток энтропии через гиперповерхность N между срезами S1 и S2 меньше модуля разности их площадей, делённого на четыре (с точностью до размерного коэффициента, равного 1 в планковской системе единиц), или равен ему. Легко видеть, что по сути это та же формула (4), только сформулированная более корректно с точки зрения геометрии.
Второе – так называемое соответствие между пространством анти-де Ситтера (adS) и Конформной теорией поля (CFT) – это реализация голографии для некоего частного случая пространств постоянной отрицательной кривизны, тесно связанная с теорией струн. Соответствие гласит, что Конформная теория поля, определённая на границе пространства-времени анти-де Ситтера (то есть на пространстве с размерностью на единицу меньше размерности самого adS), эквивалентна квантовой гравитации внутри самого анти-де Ситтера. Фактически это доказанное соответствие между высокоэнергетическими квантовыми состояниями в CFT и квантовыми возмущениями гравитационного поля в пространстве-времени постоянной отрицательной кривизны. Не забудьте, что теория струн – один из частных случаев двухмерной конформной теории поля, так что напрашиваются далеко идущие приложения. На первый взгляд,
 |
|
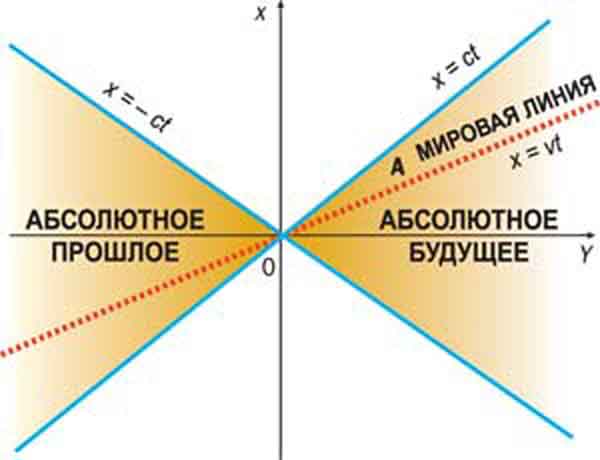
Световой конус. Событие, соответствующее началу координат в пространстве, обозначим O, а |
Пространство AdS: математический ликбез
Имеет смысл на всякий случай суммировать в отдельном посте основные факты касательно пространства AdS. В первую очередь пространство AdSd+1 — это максимально-симметричное (число параметров симметрии равно числу вращений плюс трансляций по всем координатам в плоском пределе или числу вращений в пространстве вложения в целом, то есть ½ (d + 1) (d + 2)) решение уравнений Эйнштейна с отрицательной космологической постоянной Λ. Введя радиус R пространства AdS, связанный с космологической постоянной по формуле Λ = −3/R2, можем представить AdS как вложение (d + 1)-мерного пространства-времени в (d + 2)-мерное пространство Минковского с сигнатурой (2, d):
$$y_1^2+\cdots +y_d^2-t_1^2-t_2^2=-R^2$$
Для конкретных вычислений метрики в разных координатных системах просто положим R = 1. Тогда все координаты будут безразмерными и мы получаем возможность совершать конформные преобразования и всяческие замены координат, не противоречащие размерным соображениям. Вполне очевидно что при таком описании SO (2, d) симметрия AdS становится явной.
1. Переходя к координатам Пуанкаре по формуле
$$(z,x^0,x^i)=((t_1+y_d)^{-1},t_2(t_1+y_d)^{-1},y_i(t_1+y_d)^{-1})$$
получим выражение для метрики
$$ds^2=\frac{1}{z^2}((dx^2)_{d+1}+dz^2).$$
Обратите внимание, что в такой форме имеется явная симметрия по отношению к действию подгруппы SO (1, 1) полной группы симметрий SO (2, d):
(x, z) → (cx, cz),
так что, несмотря на параметризацию d + 2 координатами, число независимых координат равно d + 1, как и должно быть. Также видна явная симметрия по отношению к SO (1, d), вращающей координаты x между собой.
В координатах Пуанкаре граница AdSd+1 представляет собой пространство Минковского R1,d−1 в z = 0 и точку P в z = ∞.
Далее, в координатах Пуанкаре можно изобразить только половину всего пространства AdS. Об этом подробнее в пункте 3.
2. Введем сферические координаты на пространственной и временной части (d + 2)-мерного пространтсва-времени вложения по-отдельности:
$$\sum _{i=1}^ddy_i^2=dv^2+v^2d\Omega _d^2,$$
$$\sum_{j=1,2}dt_j^2=d\tau ^2+\tau ^2d\theta^2.$$
Здесь dv и dτ есть элементы радиальных расстояний, а dΩd и dθ — элементы угловых расстояний. Поверхность AdS, вложенная в (d + 2)-мерное пространство-время, задается тогда формулой
$$v^2-\tau ^2=-1.$$
Из этой формулы мы можем сразу же выразить τ и dτ через v и dv, после чего получаем
$$dv^2-d\tau ^2-\tau ^2d\theta ^2=\frac{dv^2}{1+v^2}-(1+v^2)d\theta ^2.$$
Как видно у нас имеется периодичное время θ. Это нам совершенно ни к чему, поэтому мы развертываем окружность, на которой θ принимает значения, до бесконечного радиуса. Такое пространство-время называется CAdS (covering AdS). Именно оно и имеется в виду в AdS/CFT соответствии.
3. Рассмотрим глобальную параметризацию координат пространства вложения координатами пространства AdS:
$$t_1=\cosh\rho\cos\tau,\quad t_2=\cosh\rho\sin\tau,\quad y_i=\sinh\rho\,\Omega_i,$$
где i = 1, …, d, ρ ≥ 0, 0 ≤ τ < 2π, а также ∑Ωi2 = 1. Ясно, что мы имеем d + 1 независимых координат (τ, ρ, Ωi), параметризующих AdS, и метрика записывается в виде
$$ds^2=-\cosh ^2\rho\, d\tau ^2+d\rho ^2+\sinh ^2\rho\, d\Omega ^2.$$
Опять же область значений времени τ должна быть развернута до окружности с бесконечным радиусом.
Перейдем теперь от координаты θ к координате ρ по формуле tan θ = sinh ρ. Тогда 0 ≤ θ < π/2, и метрика приобретает вид
$$ds^2=\frac{1}{\cos ^2\theta}(-d\tau ^2+d\theta ^2+\sin ^2\theta\, d\Omega ^2).$$
Теперь для изучения причинной структуры и построения диаграммы Пенроуза можно совершить конформное преобразование метрики, получая:
$$ds^2=-d\tau ^2+d\theta ^2+\sin ^2\theta\, d\Omega ^2,$$
откуда будет следовать что AdS есть просто половина сферической Вселенной Эйнштейна (у Эйнштейна 0 ≤ θ < π — сферическая координата) с границей в θ = π/2, имеющей топологию сферы (в координатах Пуанкаре мы получили границу с топологией пространства Минковского, что однако просто сфера с бесконечным радиусом). Диаграмма Пенроуза для AdS2 представляет собой прямоугольник с координатами (τ, θ).
Наконец, координаты Пуанкаре, описанные в пункте 1, покрывают только половину этого прямоугольника, а именно его треугольную часть с одной из сторон, являющейся сферической границей θ = π/2 (или z = 0), а двумя другими сторонами — точечной границей z = ∞. На рисунке ниже, взятом из BBS, обозначение ρ соответсвует нашему обозначению θ.
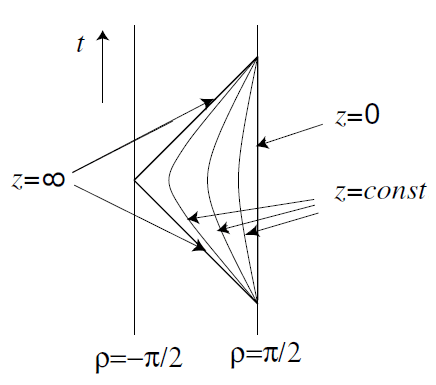
Для большинства практических целей мы будем пользоваться именно координатами Пуанкаре. Тогда мы просто накладываем нулевые граничные условия в точке P, отделяющей треугольник от всего прямоугольника AdS (на диаграмме Пенроуза P представляется в виде двух сторон треугольника, отделяющих область, покрываемую координатами Пуанкаре, от той области AdS, которую они не покрывают), так что динамику можно рассматривать только в Пуанкаре-треугольнике. Поэтому, кстати, точку P иногда называют горизонтом AdS в координатах Пуанкаре. Соответственно в глобальных координатах, в отличии от координат Пуанкаре, пространство AdS не имеет горизонта.
5. Чёрные дыры и предел делимости материи
На заре прошлого века вождь мирового пролетариата, вероятно, находясь под впечатлением открытий Резерфорда и Милликена, рождает знаменитое «электрон так же неисчерпаем, как и атом». Этот лозунг висел в кабинетах физики почти всех школ Союза. Увы, слоган Ильича так же неверен, как и некоторые его политэкономические воззрения. Действительно, «неисчерпаемость» подразумевает наличие бесконечного количества информации в любом сколь угодно малом объёме вещества V. Однако максимум информации, которую может вместить V, согласно (4) ограничен сверху.
Каким же образом существование этого предела «информационной ёмкости» должно проявляться на физическом уровне? Начнём немного издалека. Что такое современные коллайдеры, то есть ускорители элементарных частиц? По сути, это очень большие микроскопы, задача которых – увеличение разрешения по длинам Δx. А как можно улучшить разрешение? Из соотношения неопределённостей Гейзенберга
Увы, нет: непрерывно увеличивая энергию сталкивающихся частиц, он рано или поздно достигнет стадии, когда расстояние между какими-нибудь частицами из них в области столкновения станет сравнимо с соответствующим радиусом Шварцшильда, что немедленно повлечёт рождение чёрной дыры. Начиная с этого момента вся энергия будет ею поглощаться, и, сколько ни увеличивай мощность, новой информации уже не получишь. Сама же чёрная дыра при этом станет интенсивно испаряться, возвращая энергию в окружающее пространство в виде потоков субатомных частиц. Таким образом, законы чёрных дыр, вкупе с законами квантовой механики, неизбежно означают существование экспериментального предела дробления материи.
В этом смысле достижение «чернодырного» порога на коллайдерах будущего будет неизбежно означать конец старой доброй физики элементарных частиц – по крайней мере, в том виде, как она понимается сейчас (то есть как непрерывное пополнение музея элементарных частиц новыми экспонатами). Но вместо этого откроются новые перспективы. Ускорители будут служить нам уже как инструмент исследования квантовой гравитации и «географии» дополнительных измерений Вселенной (против существования которых на данный момент пока не выдвинуто каких-либо убедительных аргументов).
6. Фабрики чёрных дыр на Земле?
Итак, мы выяснили, что ускорители элементарных частиц в принципе способны производить микроскопические чёрные дыры. Вопрос: какую они должны развивать энергию, чтобы получать хотя бы одно такое событие в месяц? До недавнего времени считалось, что эта энергия чрезвычайно велика, порядка 1016 тераэлектронвольт (для сравнения: LHC сможет дать не больше 15 ТэВ). Однако если окажется, что на малых масштабах (менее 1 мм) наше пространство-время имеет число измерений больше четырёх, порог необходимой энергии значительно уменьшается и может быть достигнут уже на LHC. Причина заключается в усилении гравитационного взаимодействия, когда вступят в игру предполагаемые дополнительные пространственные измерения, не наблюдаемые при нормальных условиях. Так, если обычная сила гравитационного притяжения между массивными телами в четырёхмерном пространстве-времени обратно пропорциональна квадрату расстояния между ними, то при наличии n дополнительных компактных измерений она модифицируется в Fграв ~ 1 / r (2 + n) при r ≤ rn, где rn – максимальный размер этих измерений. Тогда с уменьшением r Fграв растёт гораздо быстрее, чем по закону обратных квадратов, и уже на расстояниях порядка
Всё вышесказанное никоим образом не означает, что мини-дыры будут получены уже на мощностях LHC – это произойдёт лишь при самом благоприятном варианте теории, которую «выберет» Природа. Кстати, не следует преувеличивать их опасность в случае получения 4 – по законам физики они быстро испарятся. Иначе Солнечная система давно прекратила бы своё существование: в течение миллиардов лет планеты бомбардируются космическими частицами с энергией на много порядков выше достигаемых на земных ускорителях.
7. Чёрные дыры и космологическая структура Вселенной
Теория струн и большинство динамических моделей Вселенной предсказывают существование особого типа фундаментального взаимодействия – глобального скалярного поля (ГСП). В масштабах планеты и Солнечной системы его эффекты крайне малы и труднообнаружимы, однако в космологических масштабах влияние ГСП возрастает неизмеримо, так как его удельная доля в средней плотности энергии во Вселенной может превышать 72 процента! Например, от него зависит, будет ли наша Вселенная расширяться вечно или в конце концов сожмётся в точку. Глобальное скалярное поле – один из вероятнейших кандидатов на роль «тёмной энергии», о которой так много пишут в последнее время.
Чёрные дыры появляются в связи с этим весьма неожиданным образом. Можно показать, что необходимость их сосуществования с глобальным скалярным полем накладывает взаимные ограничения на свойства чёрных дыр. В частности, наличие чёрных дыр накладывает ограничение на верхний предел эффективной космологической постоянной (параметра ГСП, ответственного за расширение Вселенной), тогда как ГСП ограничивает нижний предел их масс (а значит, энтропии и обратной температуры
Эпилог
Эйнштейн однажды сказал, что человеческий разум, однажды «расширенный» гениальной идеей, уже никогда не сможет сжаться до первоначального состояния 6. Это прозвучит немного парадоксально, но исследование предельно сжатого состояния материи было, есть и долгое время будет одним из главных путей и стимулов расширения границ человеческого интеллекта и познания фундаментальных законов мироздания.
ЛИТЕРАТУРА
Грищук Л. П. и др. Гравитационно-волновая астрономия: в ожидании первого зарегистрированного источника // Успехи физических наук, 2001, т. 171, № 1, http://ufn.ru/ru/articles/2001/1/a/
Новиков И. Д., Фролов В. П. Чёрные дыры во Вселенной // Успехи физических наук, 2001, т. 171, № 3, http://ufn.ru/ru/articles/2001/3/e/
Новиков И. Д. Физика чёрных дыр. – М.: Наука, 1986.
Рубаков В. А. Классические калибровочные поля. – Едиториал УРСС, 1999.
Хокинг С., Эллис Дж. Крупномасштабная структура пpoстранства-времени. – M.: Мир, 1976.
Bekenstein J. D. Lett. Nuovo Cim. 4, 737 (1972); Phys. Rev. D 7, 2333 (1973).
Susskind L. J. Math. Phys. 36, 6377 (1995).
Randall L. and Sundrum R. Phys. Rev. Lett. 83 (1999) 3370, 4690.
Zloshchastiev K. Phys. Rev. Lett. 94 (2005) 121101
Hawking S. W. Commun. Math. Phys. 43, 199 (1975).
Hooft G't. arXiv.org: gr-qc/9310026.
Bousso R. JHEP 9907, 004 (1999).
Maldacena J. M. Adv. Theor. Math. Phys. 2, 231 (1998).
Dimopoulos S. and Landsberg G. Phys. Rev. Lett. 87, 161602 (2001).
Arkani-Hamed N., Dimopoulos S. and Dvali G. R. Phys. Lett. B 429, 263 (1998); I. Antoniadis, et al, Phys. Lett. B 436, 257 (1998).
Николаев Г. Чёрные дыры. Для чего они мирозданию. – 1998, № 10,
Ройзен И. Вселенная между мгновением и вечностью. – 1996, №№ 11, 12
Семихатов А. Суперструны: на пути к теории всего . – 1997,
Сворень Р. Чёрные дыры, белые дыры. – 1983, № 10.
Транковский С. Чёрные дыры во Вселенной. – 2000, № 8,
1 Теория струн (и её обобщение,
2 Вопрос о том, испарится ли ЧД полностью, ещё обсуждается, так как тесно связан с парадоксом потери информации в ЧД, см., например, S. W. Hawking,
3 Так называемые «теоремы Хокинга-Пенроуза о сингулярностях»; см. R. Penrose, Phys. Rev. Lett. 14 (1965) 57; S. W. Hawking and R. Penrose, Proc. Roy. Soc. Lond. A 314 (1970) 529.
4 Из архива чёрного юмора физики: LHC = Last Hadron Collider.
5 Строго говоря, горизонт событий («поверхность» ЧД) является глобально определённым понятием, так как для полного его определения в общем случае нужно знать пространственную структуру Вселенной не только на данный момент, но и в будущем; см. С. Хокинг, Дж. Эллис. Крупномасштабная структура пpoстранства-времени. – M.: Мир, 1976.
6 Не правда ли, эта фраза в
• ПОДРОБНОСТИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ
ПОНЯТИЕ ЭНТРОПИИ
Согласно одной легенде, когда Клод Шеннон (Claude Shannon), гигант мысли и отец теории информации, терзался вопросом, как ему назвать только что изобретённое понятие, он попросил совета у другого гиганта, Джона фон Неймана (John von Neumann). Ответом было: «Назовите это энтропией – тогда в дискуссиях вы получите солидное преимущество – ибо никто не знает, что такое энтропия в принципе». Так родилось понятие «энтропии по Шеннону» (англ. Shannon entropy), ныне широко используемое в теории информации.
Ну что ж, уровни незнания могут быть разными – от полного невежества до глубокого понимания всей сложности проблемы. Попытаемся несколько улучшить наш уровень незнания энтропии.
Статистическая энтропия, введенная Людвигом Больцманом (Ludwig Boltzmann) в 1877 году, – это, грубо говоря, мера количества возможных состояний системы. Предположим, мы имеем две системы, состоящие из ящиков и одного шарика в каждой из них. Первая система «ящики плюс шарик» имеет только 1 ящик, вторая – 100 ящиков. Вопрос – в каком ящике находится шарик в каждой системе? Ясно, что в первой системе он может быть только в одном ящике. Помните формулу «Энтропия есть логарифм числа возможных состояний»? Тогда энтропия первой системы равна log1, то есть нулю, что отражает факт полной определённости (кстати, это одна из причин, почему в определении энтропии был использован логарифм). Что касается второй системы, то здесь мы имеем неопределённость: шарик может находиться в любом из 100 ящиков. В этом случае энтропия равна log100, то есть не равна нулю. Ясно, что, чем больше ящиков в системе, тем больше её энтропия. Поэтому и говорят часто об энтропии как о мере неопределённости, ибо наши шансы «зафиксировать» шарик в конкретном ящике уменьшаются по мере увеличения их числа.
Заметьте, что в этом вопросе нас не интересуют физические свойства ни ящиков, ни шарика (цвет, форма, масса, и прочее), то есть энтропия представляет собой понятие реляционного типа*, универсальное по своей сути и иногда (но не всегда) наделённое конкретным физическим смыслом. Мы могли бы заменить шарики электронами, а ящики – вакансиями в твёрдом теле (или даже
Термодинамическая же энтропия, предложенная в 1865 году Рудольфом Клаузиусом (Rudolf Clausius) и, как мы знаем со школы, заданная формулой
«ПАРАДОКСЫ» ЧЁРНЫХ ДЫР
В Интернете я нашёл любопытное утверждение. Его автор, Андрей, обратил внимание на несколько парадоксальных, по его мнению, аспектов физики ЧД: «Во всех книгах про чёрные дыры […] сказано, что время падения кого-либо (чего-либо) в чёрную дыру бесконечно в системе отсчёта, связанной с удалённым наблюдателем. А время испарения чёрной дыры в этой же системе отсчёта конечно, то есть тот, кто будет туда падать, не успеет этого сделать, потому что чёрная дыра уже испарится. […] Если тела падают в чёрную дыру бесконечное время, то тело, близкое по своей массе к чёрной дыре, будет сжиматься до чёрной дыры тоже бесконечное время, то есть все чёрные дыры […] расположены только в будущем по отношению к удалённому наблюдателю и их коллапс (сжатие) завершится только по прошествии бесконечного количества времени. […] Из этого утверждения следует, что никакого информационного парадокса нет – информация просто потеряется по прошествии бесконечно большого времени, но это не должно нас волновать, потому что этого принципиально нельзя дождаться…».
Это прекрасная иллюстрация главной дилеммы научно-популярной литературы – пытаясь упростить изложение, авторы книг вынуждены поступаться уровнем математической строгости. Поэтому фраза, на которой Андрей базирует свои умозаключения, «время падения кого-либо (чего-либо) в чёрную дыру бесконечно в системе отсчёта, связанной с удаленным наблюдателем», вообще говоря, неверна.
На самом деле физически корректная формулировка выглядит так: «время падения кого-либо (чего-либо) в статическую чёрную дыру бесконечно в системе отсчёта, связанной с удалённым статическим наблюдателем». Иными словами, её применимость ограничена идеализированным случаем, когда характеристики дыры неизменны во времени (то есть заведомо не тогда, когда она растёт или испаряется), а любое падающее тело предполагается пробным, достаточно малым, чтобы пренебречь изменениями дыры, вызванными его падением.
В тех же физических ситуациях, о которых говорит Андрей, как сама дыра, так и пространство-время в её окрестности не могут считаться статическими. Вследствие этого статических (по отношению к дыре) наблюдателей как таковых просто не существует. Все наблюдатели движутся и все равноправны, а «время падения кого-либо (чего-либо) в чёрную дыру», измеренное по их часам, либо конечно в их системах отсчёта, либо не определено (например, когда наблюдатель находится вне светового конуса падающего на дыру тела).
Вот таков краткий вариант ответа. Чтобы понять такие вещи на более глубоком уровне, необходим серьёзный математический аппарат (изложенный, например, в книге Хокинга и Эллиса): диаграммы Картера-Пенроуза, конформные отображения, топология многообразий и многое другое.
СИСТЕМЫ ЕДИНИЦ
В системах единиц физических измерений часть единиц принимаются за основные, а все остальные становятся производными от них. Так, например, в СИ основные единицы механики – метр, килограмм и секунда. А единица силы, ньютон, имеющая размерность кг∙м/с2, – производная от них. Размер основных единиц выбирается произвольно; их выбор определяет величину коэффициентов в уравнениях.
Во многих областях физики удобнее пользоваться так называемыми естественными системами единиц. В них за основные единицы приняты фундаментальные постоянные – скорость света в вакууме c, гравитационная постоянная G, постоянная Планка ћ, постоянная Больцмана k и другие.
В естественной системе единиц Планка принято считать c = ћ = G = k = 1. Система названа в честь немецкого физика Макса Планка, предложившего её в 1899 году. Она используется в космологии и особенно удобна для описания процессов, в которых одновременно наблюдаются и квантовые, и гравитационные эффекты, например в теории чёрных дыр и теории ранней Вселенной.
СВЕТОВОЙ КОНУС
Когда тело движется в пространстве из точки с координатами
* Кстати, именно поэтому вопрос «Так где же находится энтропия – в шарике или в ящиках?» лишён смысла.
Доктор философии (в области физики) К. ЗЛОСЧАСТЬЕВ,
Кафедра гравитации и теории поля, Институт Ядерных Исследований,
Национальный Автономный Университет Мексики
Комментарии (4):
Вот таков краткий вариант ответа. Чтобы понять такие вещи на более глубоком уровне, необходим серьёзный математический аппарат (изложенный, например, в книге Хокинга и Эллиса): диаграммы Картера-Пенроуза, конформные отображения, топология многообразий и многое другое.
Образцовый способ уйти от ответа. Тем не менее, хотя бы на пальцах, как именно и когда падающее тело пересекает горизонт событий с точки зрения наблюдателя у соседней звезды? А с точки зрения наблюдателя на круговой орбите радиусом 10^6 радиусов сферы? Я поверю на слово, просто скажите мне это слово :)
>"При их (ЧД) изучении исследователи глубоко продвинулись в научном понимании прежде сугубо философских вопросов – что есть пространство и время, существуют ли границы познания Природы"
Мною выделен важный момент. Чтоб понять (принять) важность сего, надо дать определение познанию Природы, истинно научному познанию.
Для этого надо понять, что такое НАУКА и чем она отличается от шарлотанства и др. сфер псевдознаний (включая гадания на кофейной гуще).
Но прежде чем дать определение Науки собственно, надо определить понятие базы знаний (БЗ).
БЗ называется некий набор обЪектов познания, имеющий прикладной смысл, существующие ОБЪЕКТИВНО, обЪединённый в эту БЗ согласно некому и однозначному критерию.
Ежели между обЪектами БЗ существуют связи и эти связи можно выделить, формолизовать до построения модели, увязывающей эти связи для получения прогноза, то эта БЗ с этой моделью (этими моделями) и есть то, что называется НАУКА.
Причём модель(-и) Науки не обязательно на каком-то этапе её развития должны быть математизированна(-ы), но обязательно подразумевается, что модель(-и) может быть математизированна(-ы) при соответствующем подходе.
Выделю 2-а аспекта работы с Наукой
1-е. Познание_изучение того, что уже извествно.
2-е. Расширение пространства Науки путём выявления новых связей, получение новых знаний, построение новых моделей, получение и проверка новых прогнозов, порождений новых Наук, "дочерних" по отношению к "родительской".
Теперь можно просмотреть на некоторые "науки", не являющиеся таковыми.
Например История, и, поскольку БЗ именуемая Историей не является наукой и существуют некоторые афоризмы:
-История учит нас тому, что ни чему она не учит.
-История не терпит сослогательного наклонения.
И отсюда видно, что и как надо сделать, что изменить, что сделать что бы БЗ История стала наукой.
Интересно задать вопрос:
А математика-наука?
Ответ :- Нет!! т.к. обЪекты изучения математикой собственно не имеют практического, прикладного смысла без привязки к той ли иной БЗ, без привязки к той или иной модели.
Поясню:
2х2=4 - всего лишь результат от применения некого набора правил, а вот в двух квартирах по две комнаты... всего получаем четыре комнаты- в этом есть прикладной практический смысл.
Я, при описании аспектов выделил "получение и проверка новых прогнозов" ,т.е. если проверку новых прогнозов получить невозможно в принципе, то это и есть границы познания Природы.
А это в свою очередь означает:
-Любые попытки что-либо утверждать за границами познания не научны.
Предлагаю посмотреть с этой точки зрения на любые измышления про то, что находится под горизонтом событий в ЧД, пока этот горризонт существует!
PS. Я пишу сразу в окно комментария, а в нём не предусмотренна проверка орфограффии и поэтому в моём сообщении много грамматических ошибок.
Но они не меняют сути мыслей, высказанных мною.
...Например, время жизни чёрной дыры с массой M порядка солнечной превосходит возраст Вселенной, тогда как микродыра с M = 1 тераэлектронвольт (1012 эВ, примерно
Здесь выше в цитате допущена ошибка в минимальной массе чёрной дыры. Как может быть масса самой маленькой чёрной дыры меньше половины планковской, т.е меньше 0,01 миллиграмма? Автор ошибся на целых 22 порядка.!!!
Кроме того мини-черная дыра с массой 0,01 мг "живёт" всего лишь порядка 10 в минус 43 степени секунд, т.е. "живёт" минимально возможное время, меньше которого квантовая механика не допускает. Автор промахнулся на 16 порядков!!! А ведь автор статьи прекрасно знает естесственную систему единиц Планка. Ниже я цитирую его слова:
"...В естественной системе единиц Планка принято считать c = ћ = G = k = 1. ... Она используется в космологии и особенно удобна для описания процессов, в которых одновременно наблюдаются и квантовые, и гравитационные эффекты, например в теории чёрных дыр и теории ранней Вселенной..."
Вот дык дают учёные в Мексике!
Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.