Существует два фундаментальных аспекта общей теории относительности Эйнштейна — принцип относительности, который гласит, что законы физики не чувствительны к разнице между покоем и равномерным движением, и принцип эквивалентности, который сообщает нам, как следует модифицировать эти идеи, чтобы включить в рассмотрение гравитационное поле.

Мы должны теперь обратиться к третьей фундаментальной составляющей теории Эйнштейна — конечной скорости света. Замечательно, что все эти три фундаментальные составляющие восходят еще к Галилею, поскольку он был, видимо, первым, кто имел настолько ясное представление о конечной скорости распространения света, что предпринимал реальные шаги для измерения этой скорости. Способ, предложенный им в 1638 году, состоял в синхронизации вспышек фонарей, расположенных на удаленных друг до друга холмах, и, как мы теперь понимаем, был слишком грубым.

Галилей не мог предвидеть той необычайно высокой скорости, с которой действительно распространяется свет. Галилей и Ньютон, по-видимому, имели сильное подозрение относительно возможной глубокой связи между природой света и теми силами, которые связывают материю воедино. Однако должной реализации этих предчувствий пришлось ждать до двадцатого века, когда была вскрыта истинная природа сил химической связи и сил, которые удерживают вместе отдельные атомы. Сейчас мы знаем, что эти силы имеют фундаментальное электромагнитное происхождение (они обусловлены взаимодействием электромагнитного поля с заряженными частицами) и что теория электромагнетизма есть также теория света.

Для понимания атомов и химии необходимы еще дополнительные ингредиенты, предоставляемые квантовой теорией, однако основные уравнения, описывающие электромагнетизм и свет, были сформулированы в 1865 году великим шотландским физиком Джеймсом Клерком Максвеллом, который был вдохновлен великолепными экспериментальными открытиями Майкла Фарадея, сделанными 30 годами раньше. Теория Максвелла требует, чтобы скорость света была определенной фиксированной величиной, которая обычно обозначается буквой $c$ и составляет в обычных единицах $3\cdot 10^{8}$ метров в секунду. Здесь, однако, возникает проблема, если мы хотим сохранить принцип относительности. Здравый смысл вроде бы говорит нам, что если скорость света, измеряемая одним наблюдателем в своей системе отсчета, равна с, то другой наблюдатель, который движется с очень высокой скоростью относительно первого, измерит другую скорость распространения света, большую или меньшую в зависимости от того, как движется второй наблюдатель. Но принцип относительности требует, чтобы физические законы для второго наблюдателя (которые определяют, в частности, ту скорость света, которую воспринимает второй наблюдатель) были точно такими же, как и для первого наблюдателя. Это кажущееся противоречие между постоянством скорости света и принципом относительности привело Эйнштейна (а также фактически раньше голландского физика Гендрика Антоона Лоренца и, в более законченной форме, французского математика Анри Пуанкаре) к замечательной точке зрения, полностью устраняющей это противоречие.

Как это получается? Естественно считать, что имеется неразрешимый конфликт между требованиями 1) теории максвелловского типа, в которой существует абсолютная скорость света, и 2) принципа относительности, согласно которому вид физических законов не зависит от скорости движения системы отсчета, используемой для их описания. Потому что разве нельзя выбрать систему отсчета, движущуюся со скоростью, близкой к скорости света или даже превышающей ее? И разве скорость света, воспринимаемая в такой системе отсчета, может оставаться прежней? Это несомненное противоречие не возникает в теории, поддерживаемой Ньютоном (и, как я предполагаю, Галилеем), согласно которой свет ведет себя как частицы, скорость которых зависит, таким образом, от скорости источника. Поэтому Галилей и Ньютон могли жить в полном согласии с принципом относительности. Но со временем такой взгляд на природу света вступил в противоречие с наблюдениями удаленных двойных звезд, показавшими, что скорость света не зависит от скорости его источника. С другой стороны, набрала силу теория Максвелла — не только из-за мощной поддержки со стороны эксперимента (наиболее важными были опыты Генриха Герца в 1888 году), но и благодаря притягательности и универсальному характеру самой теории, объединяющей законы, управляющие электрическим полями, магнитными полями и светом, в единую математическую схему, обладающую замечательным изяществом и существенной простотой. В теории Максвелла свет представляет собой не частицы, а волны, и мы вынуждены столкнуться с тем фактом, что в этой теории существует фиксированная скорость, с которой должны распространяться световые волны.

Световые конусы

Точка зрения, основанная на геометрии пространства-времени, открывает нам исключительно ясный путь к разрешению противоречия, создаваемого конфликтом между теорией Максвелла и принципом относительности. Как уже отмечалось, эта пространственно- временная точка зрения первоначально не использовалась Эйнштейном (а также Лоренцем и, видимо, даже Пуанкаре). Однако в ретроспективе видна мощь этого подхода. Отбросим на время гравитацию и все сопутствующие ей тонкости и усложнения, связанные с принципом эквивалентности. Начнем с чистого листа, то есть с вещественного 4-многообразия без особенностей. Мы хотим посмотреть, что означает утверждение о существовании фундаментальной скорости, каковой должна быть скорость света. В любой точке пространства-времени $p$ (изображающей некоторое «событие») можно рассмотреть семейство всех различных лучей света, проходящих через эту точку во всевозможных пространственных направлениях. Пространственно-временное описание дает семейство мировых линий, проходящих через точку $p$ (см. рис. 17.10 а, б).

Рис. 17.10. Световой конус определяет фундаментальную скорость света. Истории фотонов, проходящих через пространственно-временную точку (событие) $p$. а) В чисто пространственных терминах световым конусом (конусом будущего) является сфера, расширяющаяся во все стороны от точки $p$ (волновые фронты), б) В пространственно-временной формулировке истории фотонов, испускаемых в точке $p$, образуют световой конус с вершиной в точке $p$. в) Поскольку далее нам придется рассматривать искривленное пространство-время, полезно рассматривать конус (часто называемый нулевым конусом в точке $p$) как локальную структуру в пространстве-времени, т. е. в касательном пространстве $T_p$ в точке $p$

Удобно назвать эти мировые линии «историями фотонов», проходящих через точку $p$, хотя теория Максвелла рассматривает свет как волновое явление. По разным причинам это не приводит к сколько-нибудь существенному конфликту. В теории Максвелла «фотон» можно рассматривать как очень малый сгусток электромагнитного возмущения очень высокой частоты, который будет вести себя, вполне адекватно нашим целям, как малая частица, распространяющаяся со скоростью света. (Вместо этого можно рассматривать «волновые фронты», то, что математики называют «бихарактеристиками», или же можно предпочесть обратиться к квантовой теории, согласно которой свет можно также рассматривать состоящим из «частиц», действительно называемых «фотонами».)

В окрестности точки $p$ семейство историй фотонов, проходящих через точку $p$, образует конус в пространстве-времени, называемый «световым конусом» в точке $p$. Чтобы скорость света была фундаментальной, в пространственном представлении необходимо придать фундаментальный смысл световым конусам. С точки зрения, принятой в геометрии многообразий, часто бывает удобнее рассматривать «световой конус» как структуру в касательном пространстве $T_p$ в точке $p$ (см. рис. 17.10 в). (Нас в конечном счете интересуют скорости в точке р, а скорость есть объект, определяемый в касательном пространстве.) Эту структуру в касательном пространстве часто называют нулевым конусом, , а термин «световой конус» сохранить для геометрического места световых лучей, проходящих через точку $p$ в пространстве-времени. Заметим, что световой конус (или нулевой конус) состоит из двух частей — конуса прошлого и конуса будущего. Конус прошлого можно рассматривать как историю вспышки света, сходящейся в точку $p$ (все световые лучи одновременно приходят в эту пространственно-временную точку); аналогично конус будущего представляет историю вспышки света от взрыва в пространственно-временной точке $p$ (см. рис. 17.11).

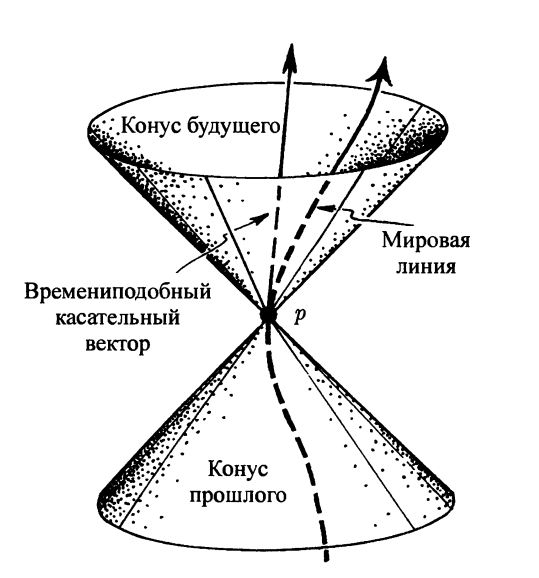
Рис. 17.11. Конус прошлого и конус будущего. Нулевой конус прошлого (или нулевые векторы прошлого) относится к свету, сходящемуся в точку $p$, подобно тому как конус будущего (нулевые векторы будущего) относится к свету, возникающему в точке $p$. Мировая линия любой массивной частицы в точке $p$ имеет времениподобный касательный вектор (направленный в будущее) и лежит внутри нулевого конуса будущего в точке $p$.

Как математически описать нулевой конус в точке $p$? Потребуем, чтобы в точке $p$ скорость света была одинаковой во всех направлениях, так чтобы пространственная конфигурация, окружающая эту точку спустя мгновение после вспышки света, имела сферическую, а не какую-нибудь яйцевидную форму (форму овоида). Говоря «спустя мгновение», я имею в виду, что такое рассмотрение применимо к бесконечно малой временной (а также пространственной) окрестности точки $p$; это позволяет считать такие конфигурации структурами в касательном пространстве в точке $p$. Утверждение, что нулевой конус выглядит «сферическим», означает всего лишь то, что конус определяется уравнением в касательном пространстве, которое является квадратичным. Это означает, что уравнение имеет вид $$g_{\mu\nu}v^{\mu}v^{\nu}=0$$ где $g_{\mu\nu}$ — индексная форма некоторого несингулярного симметричного [$\left ( ^0_2 \right)$-тензора $\boldsymbol{g}$ с лоренцевой сигнатурой $(+--)$. Термин «нулевой» (конус) указывает на то, что вектор $\boldsymbol{v}$ имеет нулевую длину $(|\boldsymbol{v}|^2 = 0)$ в данной (псевдо)метрике $\boldsymbol{g}$.

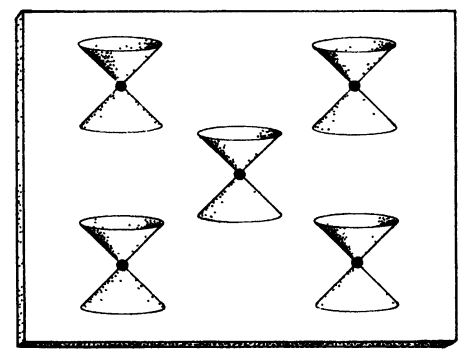
Рис. 17.12. Пространство Минковского $\mathbb{M}$ является плоским, и его нулевые конусы распределены равномерно; все они изображены параллельными.

На этой стадии мы касаемся тензора $\boldsymbol{g}$ только в связи с его ролью в определении нулевых конусов в соответствии с вышеприведенным уравнением. Если умножить $\boldsymbol{g}$ на какое-либо вещественное число, отличное от нуля, мы получим прежний нулевой конус. Вскоре мы потребуем, чтобы тензор $\boldsymbol{g}$ играл более важную физическую роль в определении метрики пространства-времени, поэтому нам понадобится соответствующий масштабный множитель, но пока что мы будем иметь дело лишь с семейством нулевых конусов, по одному в каждой точке пространства-времени. Чтобы можно было утверждать, что скорость света постоянна, примем, что имеет смысл считать нулевые конусы различных событий параллельными друг другу, поскольку «скорость» в пространственных терминах соответствует «наклону» в пространственно-временных терминах. Это приводит нас к картине пространства-времени, изображенной на рис. 17.12.

Нет комментариев.

Только зарегистрированные пользователи могут оставлять комментарии. Войдите или зарегистрируйтесь пожалуйста.