Введение
1. На Земле наблюдалась вспышка сверхновой в туманности Андромеда. Оцените, сколько времени прошло с момента взрыва звезды.
2.
В момент наблюдения галактика находится на расстоянии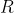 
от нас и удаляется со скоростью 
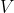. На каком расстоянии она находилась в момент излучения наблюдаемого света?
3. Оценить длину свободного пробега атома водорода в межгалактическом пространстве.
4.
Участники космической гонки - протоны, ускоренные на LHC )
и фотоны; дистанция Земля - Солнце. На сколько отстанут протоны по времени и по расстоянию?
5. Выразить боровский радиус через постоянную тонкой структуры и комптоновскую длину волны.
6. Чему равна максимальная сумма углов на сфере?
7. На поверхности двумерной сферы радиуса $R$ проведена окружность, имеющая радиус $r$, если измерять его по поверхности сферы. Найдите длину этой окружности как функцию $r$.
8.
Предположим, что галактики распределены равномерно на поверхности двумерной сферы радиуса R с плотностью 
галактик на единицу площади. Определить полное число галактик N внутри радиуса r. Если геометрия не плоская, а сферическая, то больше или меньше галактик видны в пределах данного радиуса?
9.
Объект имеет размер A, а расстояние до него B. Определить угол, под которым виден объект в плоском пространстве и в пространствах постоянной отрицательной и положительной кривизны.
10. Каждую секунду на квадратный метр Земли падает около $1400 Дж. солнечной энергии. Оценить абсолютную светимость Солнца.
11.
Считая, что продолжительность стадии постоянной светимости Солнца порядка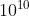 
лет, найти, какую долю своей массы Солнце потеряло за счёт излучения.
12. Почему связь между светимостью цефеид (класс переменных звёзд с довольно точной зависимостью период-светимость) и периодом изменения их блеска была открыта по наблюдению звёзд в Большом Магеллановом Облаке (спутник нашей Галактики), а не в нашей Галактике?
13.
Сверхновая в максимуме блеска достигает абсолютной звёздной величины M=-21. Как часто будут регистрироваться вспышки сверхновых, если наблюдение ведётся по всему небу до предельной величины m=14? Считать, что в типичной галактике сверхновая вспыхивает в среднем один раз за 100 лет, а галактики распределены в пространстве с плотностью одна галактика на 
.
14.
Из фундаментальных констант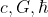 
построить величины размерности длины, времени, массы, температуры, плотности и найти их значения (соответствующие величины называются планковскими единицами).
15. Во сколько раз время запаздывания восприятия объекта, находящегося на расстоянии 1 метр от плоского зеркала, больше планковского времени?
16.
Показать, что для частицы планковской массы комптоновская длина волны совпадает с гравитационным радиусом 
(гравитационный радиус в общей теории относительности (ОТО) совпадает с радиусом сферически-симметричного тела, для которого в классической механике вторая космическая скорость на поверхности была бы равна скорости света).
17. Каков гравитационный радиус Вселенной? Сравните его с размером наблюдаемой Вселенной.
18.
Показать, что в единицах 
19.
Выразить 
в 
20.
Показать, что постоянная тонкой структуры безразмерна только в пространстве размерности D=3.
